A vessel in the shape of a hollow hemisphere surmounted by a once is held with the axis vertical and vertex uppermost. If it be filled with a liquid so as to submerge half the axis of the cone in the liquid, and the height of the cone be double the radius of its base, find the liquid on the vessel is x times the weight of the liquid that the hemisphere can hold.
15/8
1/8
5/8
15/2
The correct Answer is:A
To solve the problem, we need to find the ratio x of the weight of the liquid in the vessel to the weight of the liquid that the hemisphere can hold. We will break down the problem step by step:
Step 1: Understand the Geometry
The vessel consists of a hollow hemisphere and a cone on top. Let the radius of the hemisphere be r. The height of the cone is given as twice the radius of its base, which is also r. Therefore, the height of the cone is 2r.
Step 2: Determine the Volume of Liquid in the Vessel
The liquid fills the cone to a height of r (half the height of the cone). We need to find the volume of the liquid in both the cone and the hemisphere.
Volume of the cone filled with liquid:
The volume V of a cone is given by:
V=13πr2h
For our cone, the radius at the height r can be determined using similar triangles. The radius at height r is r2 (since the height of the cone is 2r). Thus, the volume of the liquid in the cone is:
Vcone=13π(r2)2r=13πr24r=πr312
Step 3: Volume of the Hemisphere
The volume of the hemisphere is given by:
Vhemisphere=23πr3
Step 4: Total Volume of Liquid in the Vessel
The total volume of liquid in the vessel is the sum of the volume of the liquid in the cone and the volume of the hemisphere:
Vtotal=Vcone+Vhemisphere=πr312+23πr3
To add these volumes, we need a common denominator:
23πr3=812πr3
Thus,
Vtotal=πr312+8πr312=9πr312=3πr34
Step 5: Weight of the Liquid in the Vessel
The weight of the liquid in the vessel can be calculated using the formula:
Wliquid=density×volume×g
Let the density of the liquid be ρ. Therefore,
Wliquid=ρ⋅3πr34⋅g
Step 6: Weight of the Liquid the Hemisphere Can Hold
The weight of the liquid that the hemisphere can hold is:
Whemisphere=ρ⋅23πr3⋅g
Step 7: Find the Ratio x
We need to find the ratio x such that:
Wliquid=x⋅Whemisphere
Substituting the expressions we derived:
ρ⋅3πr34⋅g=x⋅(ρ⋅23πr3⋅g)
Canceling out common terms:
34=x⋅23
Solving for x:
x=34⋅32=98
Conclusion
Thus, the value of x is:
98
The vessel consists of a hollow hemisphere and a cone on top. Let the radius of the hemisphere be r. The height of the cone is given as twice the radius of its base, which is also r. Therefore, the height of the cone is 2r.
The liquid fills the cone to a height of r (half the height of the cone). We need to find the volume of the liquid in both the cone and the hemisphere.
The volume V of a cone is given by:
V=13πr2h
For our cone, the radius at the height r can be determined using similar triangles. The radius at height r is r2 (since the height of the cone is 2r). Thus, the volume of the liquid in the cone is:
Vcone=13π(r2)2r=13πr24r=πr312
The volume of the hemisphere is given by:
Vhemisphere=23πr3
The total volume of liquid in the vessel is the sum of the volume of the liquid in the cone and the volume of the hemisphere:
Vtotal=Vcone+Vhemisphere=πr312+23πr3
23πr3=812πr3
Thus,
Vtotal=πr312+8πr312=9πr312=3πr34
The weight of the liquid in the vessel can be calculated using the formula:
Wliquid=density×volume×g
Let the density of the liquid be ρ. Therefore,
Wliquid=ρ⋅3πr34⋅g
The weight of the liquid that the hemisphere can hold is:
Whemisphere=ρ⋅23πr3⋅g
We need to find the ratio x such that:
Wliquid=x⋅Whemisphere
Substituting the expressions we derived:
ρ⋅3πr34⋅g=x⋅(ρ⋅23πr3⋅g)
Canceling out common terms:
34=x⋅23
Solving for x:
x=34⋅32=98
Thus, the value of x is:
98
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - DISHA PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-1 CONCEPT BUILDER
59 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
- MOTION IN A PLANE BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -2 : CONCEPT APPLICATOR
28 Videos
Similar Questions
A conical vessel wihout a bottom stands on a table. A liquid is poured with the vessel & as soon as the level reaches h, the pressure of the liquid raises the vessel. The radius of the base of the vessel is R and half angle of the cone α and the weight of the vessel is W. What is the density of the liquid ?

View SolutionTo what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
View Solution
Knowledge Check
A toy is in the. shape of a hemisphere surmounted by a cone. If radius of base.of the cone is 3 cm and height is 4cm. The total surface area of the toy is:
A33πcm2B42πcm2C66πcm2D56πcm2The height to which a cylindrical vessel be filled with a homogenous liquid, to make the average force with which the liquid presses the side of the vessel equal to the force exerted by the liquid on the bottom of the vessel, is equal to.
Ahalf of the radius of the vesselBradius of the vesselCone-fourth of the radius of the vesselDthree-fourth of the radius of the vessel.A cylindrical vessel of radius r is filled with a homogeneous liquid upto a height h. It is found that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder. What is the relation between r and h?
Ar=h2Br=hCr=2hDr=32h
A metallic hemisphere is melted and recast in the shape of a cone with the ame base radius (R) as that of the hemisphere. If H is the height of the cone, then :
View SolutionTo what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
View SolutionTo what height h should a cylindrical vessel of diameter d be filled with a liquid so that the total force on the vertical surface of the vessel be equal to the force on the bottom-
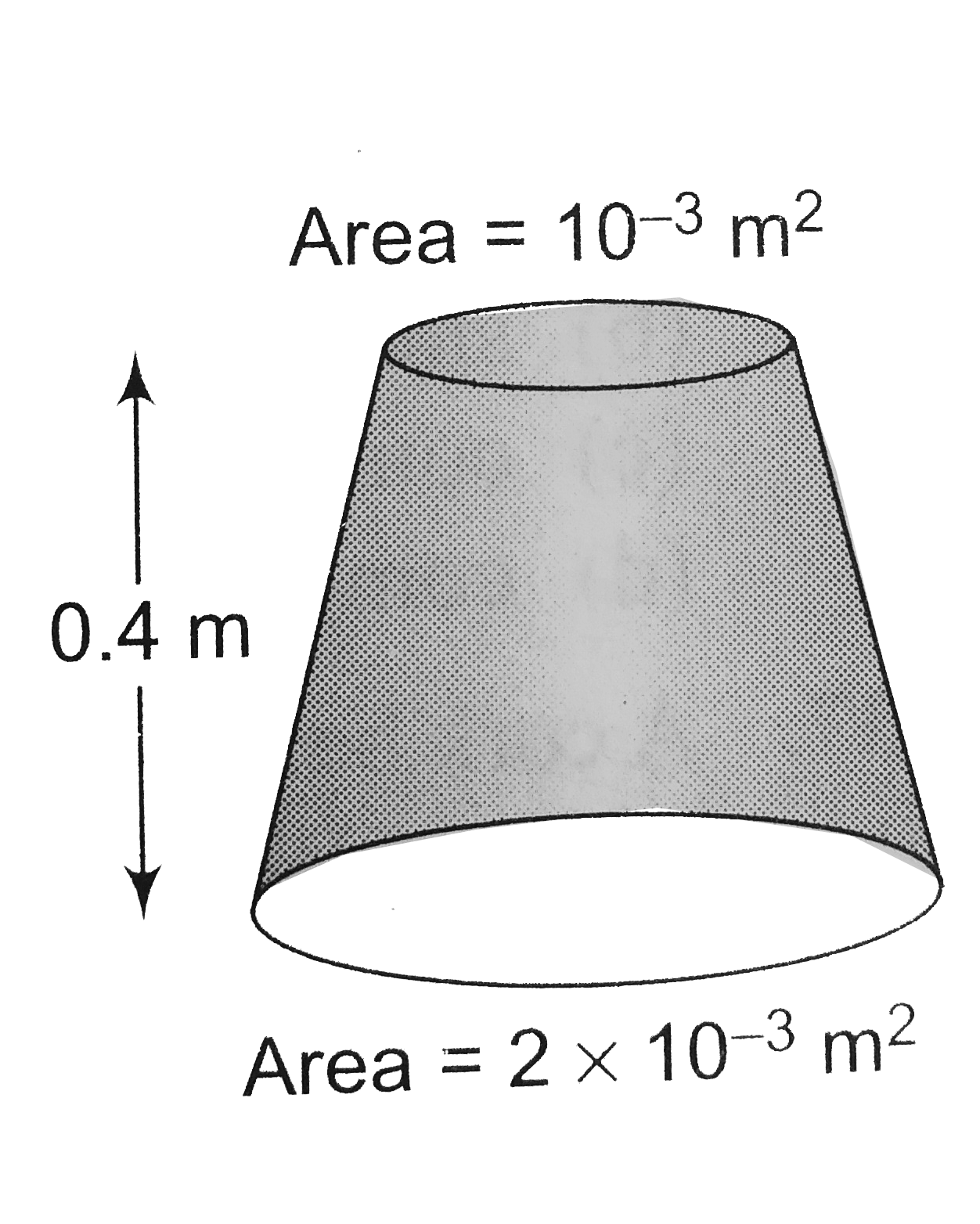
View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
View SolutionA metallic hemisphere is melted and reast in the shape of a cone with the same base radius (R ) as that of the hemisphere.If H is the height of the cone,then:
View Solution
