A cork is submerged in water by a spring attached to the bottom of a bowl. When the bowl is kept in an elevator moving with acceleration downwards, the length of spring.
increases
decreases
remain unchanged
none of these
The correct Answer is:B
To solve the problem of how the length of the spring changes when the bowl with the submerged cork is in an elevator moving downwards, we can follow these steps:
1. Understand the Setup:
- We have a cork submerged in water, held down by a spring attached to the bottom of a bowl.
- The bowl is placed in an elevator that is accelerating downwards.
2. Identify Forces Acting on the Cork:
- The forces acting on the cork include:
- The buoyant force (thrust) acting upwards.
- The weight of the cork acting downwards.
3. Consider the Effect of Downward Acceleration:
- When the elevator accelerates downwards, the effective gravitational acceleration acting on the cork changes.
- The effective acceleration can be expressed as g′=g−a, where g is the acceleration due to gravity and a is the downward acceleration of the elevator.
4. Calculate the Buoyant Force:
- The buoyant force (thrust) acting on the cork can be given by the formula:
Fb=ρVg′
- Substituting for g′:
Fb=ρV(g−a)
- Here, ρ is the density of the fluid (water), V is the volume of the cork, and g′ is the effective gravitational acceleration.
5. Analyze the Change in Buoyant Force:
- As the elevator accelerates downwards, g′ decreases, which means the buoyant force Fb also decreases.
- This decrease in buoyant force results in less upward force acting on the cork.
6. Effect on the Spring:
- Since the buoyant force acting on the cork is reduced, the spring will not need to exert as much force to keep the cork submerged.
- As a result, the length of the spring will increase (it will stretch more) to accommodate the reduced buoyant force.
7. Conclusion:
- Therefore, when the elevator is moving downwards, the length of the spring will increase.
Final Answer:
The length of the spring will increase when the bowl is kept in an elevator moving downwards.
- We have a cork submerged in water, held down by a spring attached to the bottom of a bowl.
- The bowl is placed in an elevator that is accelerating downwards.
- The forces acting on the cork include:
- The buoyant force (thrust) acting upwards.
- The weight of the cork acting downwards.
- When the elevator accelerates downwards, the effective gravitational acceleration acting on the cork changes.
- The effective acceleration can be expressed as g′=g−a, where g is the acceleration due to gravity and a is the downward acceleration of the elevator.
- The buoyant force (thrust) acting on the cork can be given by the formula:
Fb=ρVg′
- Substituting for g′:
Fb=ρV(g−a)
- Here, ρ is the density of the fluid (water), V is the volume of the cork, and g′ is the effective gravitational acceleration.
- As the elevator accelerates downwards, g′ decreases, which means the buoyant force Fb also decreases.
- This decrease in buoyant force results in less upward force acting on the cork.
- Since the buoyant force acting on the cork is reduced, the spring will not need to exert as much force to keep the cork submerged.
- As a result, the length of the spring will increase (it will stretch more) to accommodate the reduced buoyant force.
- Therefore, when the elevator is moving downwards, the length of the spring will increase.
The length of the spring will increase when the bowl is kept in an elevator moving downwards.
Topper's Solved these Questions
Similar Questions
A block is fully submerged in a vessel filled with water by a spring attached to the bottom of the vessel. In equilibrium position spring is compressed. If the vessel now moves downwards with an acceleration a(<g). What happens to the length of the spring.?

View SolutionA spring of force constant 200Nm−1 has a block of mass 10 kg hanging at its one end and the other end of the spring is attached to the celling of an elevator. The elevator is rising upwards with an acceleration of g4 and the block is in equilibrium with respect to the elevator . when the acceleration of the elevator suddenly ceases , the block starts oscillating . What is the amplitude (in m) of these oscillations ?
View Solution
Knowledge Check
A spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads 49 N, when the lift is stationary. If the moves downwards with an acceleration of 5 ms−2, then reading of the spring balance will be
A49 NB24 NC74 ND15 NA spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads 49N, when the lift is stationary. If the lift moves downward with an acceleration of 5m/22, the reading of the spring balance will be
A(a) 24NB(b) 74NC(c) 15ND(d) 49NA spring of spring constant 200N/m has a block of mass 1kg hanging at its one end and other end of spring is attached to ceiling of an elevator. The elevator is rising upwards with an acceleration g/3. What should be the angular frequency and elongation during the time when the elevator is accelerating?
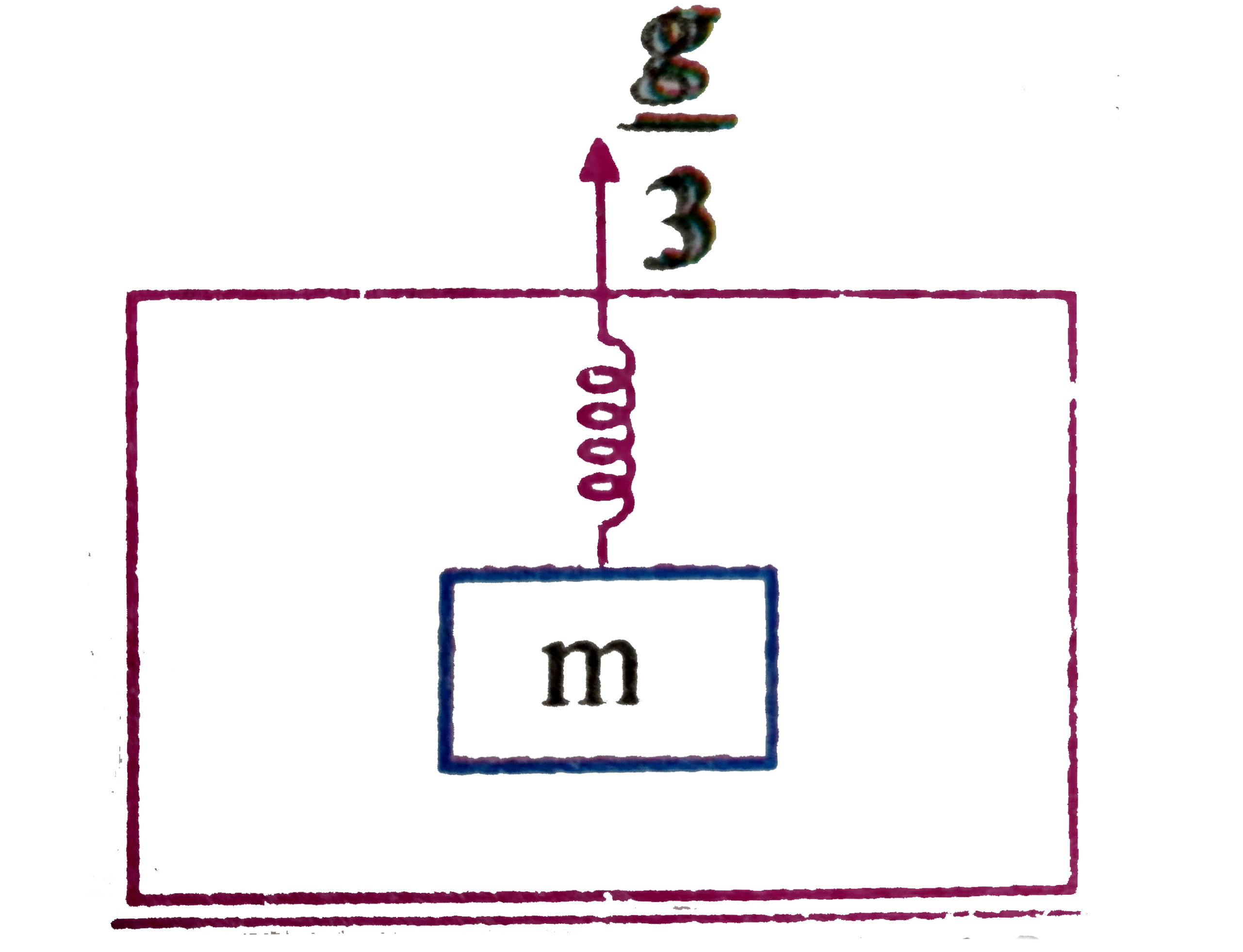 A14.14rad/s,0.07mB13rad/s,0.1mC14rad/s,0.05D10rad/s,0.07
A14.14rad/s,0.07mB13rad/s,0.1mC14rad/s,0.05D10rad/s,0.07
An iron sphere is suspended with a spring. The length of the spring increases. When the sphere is completely in water, the extension in the length of the spring decreases. Why does it happen so?
View SolutionA spring of force constant 200Nm−1 has a block of mass 10 kg hanging at its one end and the other end of the spring is attached to the celling of an elevator. The elevator is rising upwards with an acceleration of g4 and the block is in equilibrium with respect to the elevator . when the acceleration of the elevator suddenly ceases , the block starts oscillating . What is the amplitude (in m) of these oscillations ?
View SolutionA spring of spring constant 200N/m has a block of mass 1kg hanging at its one end and form the other and the spring is attached to a celling of an elevator. The elevator rises upwards with an acceleration of g/3.
When acceleration is suddenly ceased , then what should be the angular frequency and elongation during the time when the elevator is accelerating?

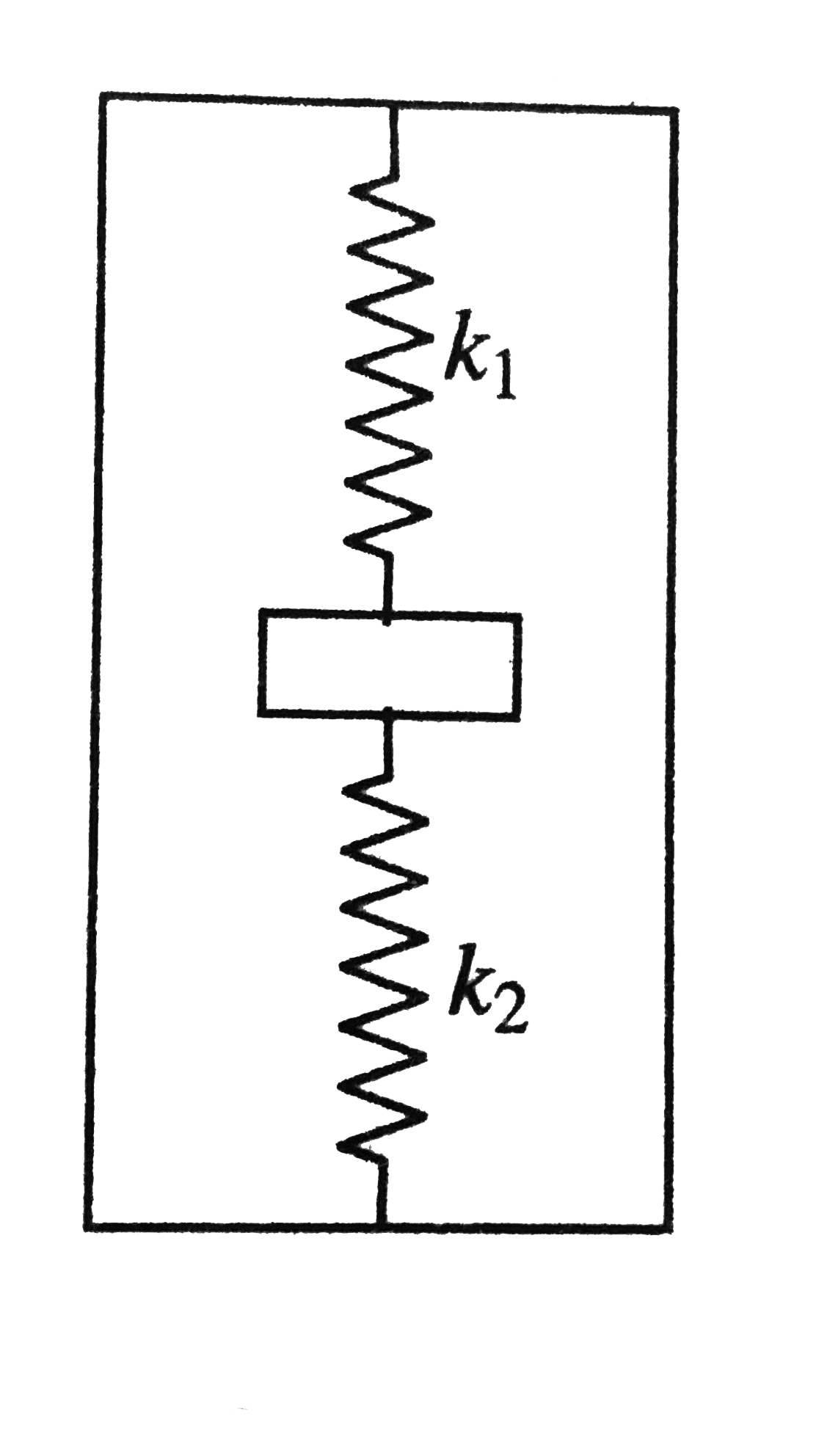
View SolutionOne end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
View SolutionAn engineer is designing a spring to be placed at the bottom of an elevator shaft, if the elevator cable should break at a height h above the top of the spring, calculate the required value of the spring constant k, so that passsengers undergo an acceleration of no more than 10 g when brought to rest, Let M be the total mass of the elevator and passengers
View Solution