A gas may expand either adiabatically or isothermally. A number of p−V curves are drawn for the two processes over different ranges of pressure and volume, it will be found that
(i) Two adiabatic curves do not intersect
(ii) two isothermal curves do not intersect
(iii) an adiabatic curve and an isothermal curve may intersect.
(iv) the magnitude of the slope of an adiabatic curve is greater thanthe magnitude of the slope of an isothermal curve
(i),(ii)
(ii),(iii)
(iii),(iv)
all
The correct Answer is:D
To analyze the statements regarding the behavior of adiabatic and isothermal processes in a gas, let's go through each statement step by step.
1. Statement (i): Two adiabatic curves do not intersect.
- Explanation: In an adiabatic process, there is no heat exchange with the surroundings. Each adiabatic curve corresponds to a different amount of internal energy, which is a function of the temperature of the gas. If two adiabatic curves were to intersect, it would imply that the gas could exist at the same pressure and volume with two different temperatures, which is not possible. Therefore, this statement is true.
2. Statement (ii): Two isothermal curves do not intersect.
- Explanation: An isothermal process occurs at a constant temperature. Each isothermal curve represents a different temperature. If two isothermal curves intersected, it would mean that at the same pressure and volume, the gas could have two different temperatures, which contradicts the definition of isothermal processes. Thus, this statement is also true.
3. Statement (iii): An adiabatic curve and an isothermal curve may intersect.
- Explanation: It is possible for an adiabatic curve and an isothermal curve to intersect because they represent different thermodynamic processes. An intersection would imply that at a certain pressure and volume, the gas can be at a specific temperature (isothermal) while also undergoing an adiabatic change. Therefore, this statement is true.
4. Statement (iv): The magnitude of the slope of an adiabatic curve is greater than the magnitude of the slope of an isothermal curve.
- Explanation: To understand the slopes mathematically:
- For an adiabatic process, the relationship is given by PVγ=k (where γ=Cp/Cv). Differentiating gives us:
dPdV=−γPV
- For an isothermal process, the relationship is PV=k. Differentiating gives us:
dPdV=−PV
- Comparing the two slopes, we see that the slope of the adiabatic curve is steeper (more negative) than that of the isothermal curve because γ>1. Therefore, this statement is true.
Summary of Truth Values:
- (i) True
- (ii) True
- (iii) True
- (iv) True
- Explanation: In an adiabatic process, there is no heat exchange with the surroundings. Each adiabatic curve corresponds to a different amount of internal energy, which is a function of the temperature of the gas. If two adiabatic curves were to intersect, it would imply that the gas could exist at the same pressure and volume with two different temperatures, which is not possible. Therefore, this statement is true.
- Explanation: An isothermal process occurs at a constant temperature. Each isothermal curve represents a different temperature. If two isothermal curves intersected, it would mean that at the same pressure and volume, the gas could have two different temperatures, which contradicts the definition of isothermal processes. Thus, this statement is also true.
- Explanation: It is possible for an adiabatic curve and an isothermal curve to intersect because they represent different thermodynamic processes. An intersection would imply that at a certain pressure and volume, the gas can be at a specific temperature (isothermal) while also undergoing an adiabatic change. Therefore, this statement is true.
- Explanation: To understand the slopes mathematically:
- For an adiabatic process, the relationship is given by PVγ=k (where γ=Cp/Cv). Differentiating gives us:
dPdV=−γPV
- For an isothermal process, the relationship is PV=k. Differentiating gives us:
dPdV=−PV
- Comparing the two slopes, we see that the slope of the adiabatic curve is steeper (more negative) than that of the isothermal curve because γ>1. Therefore, this statement is true.
- (i) True
- (ii) True
- (iii) True
- (iv) True
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A gas may expand either abiabatically or isothermally .A number of P-V curves are drawn for the two processes over different ranges of pressure and volume . It will be found that :
AAn adiabatic curve and an isothermal curve may intersectBTwo adiabatic curves do not intersactCTwo isothermal curves do not intersectDAll of these - Question 2 - Select One
A gas may expand either abiabatically or isothermally .A number of P-V curves are drawn for the two processes over different ranges of pressure and volume . It will be found that :
Atwo adiabtaic curves do not intersect.Btwo isothermal curves do not intersect.Can adiabatic curve and an isothermal curve may intresect.Dthe magniture of the slpoe of an adiabatic curvesis greater than the magnitude of the slope of an isothermal curves for the same values of pressure and volume. - Question 3 - Select One
Can two isothermal curves cut each other
ANeverByesCThey will cut when temperature is 0∘CDYes, when the pressure is critical pressure
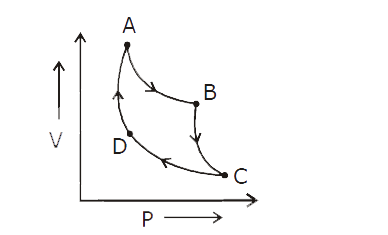
If DA and BC are adiabatic curves and AB and CD are isothermal curves then :–
 View Solution
View SolutionShow that the slope of adiabatic curve at any point is λ times the slope of an isothermal curve at the corresponding point.
View SolutionThe ratio of slopes of adiabatic and isothermal curves is
View SolutionThe slope of isothermal and adiabatic curves are related as
View SolutionIn the given graph, adiabatic and isothermal curves are shown. Then,
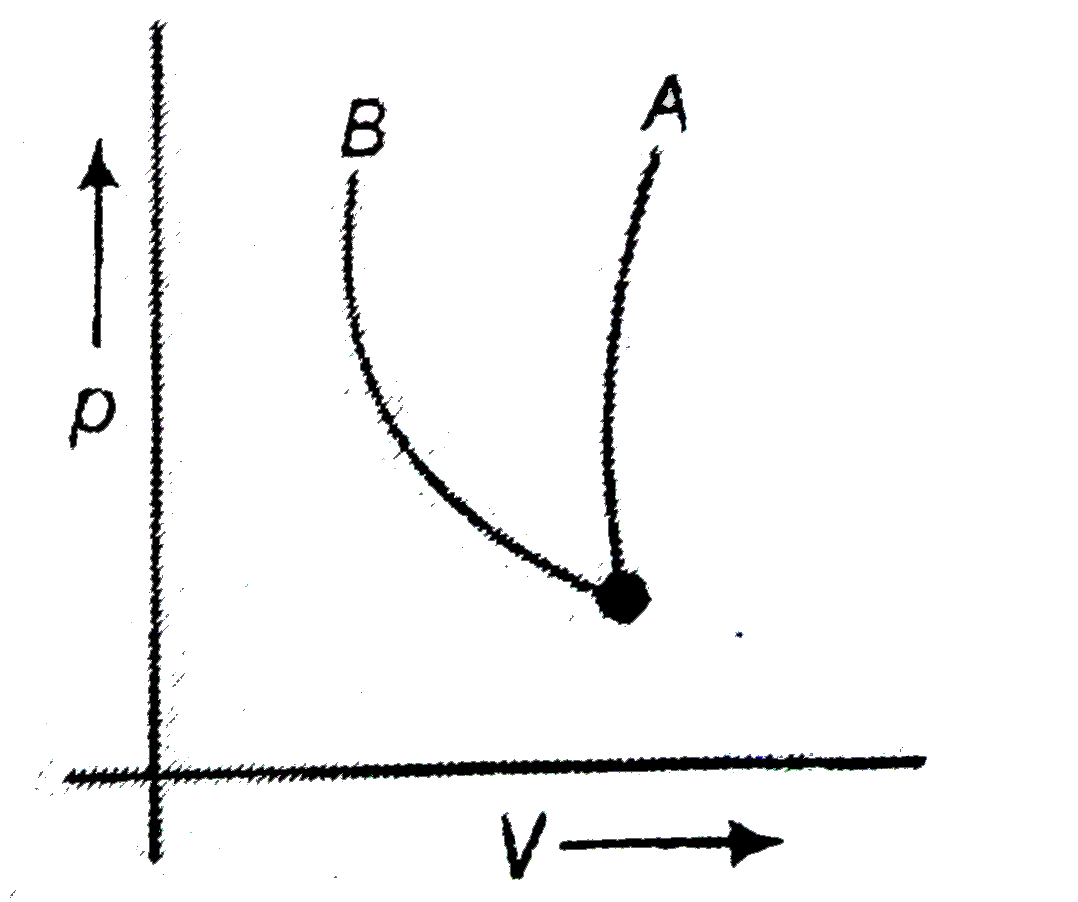 View Solution
View Solution

