The slope of isothermal and adiabatic curves are related as
isothermal curve slope = adiabatic curve slope
isothermal curve slope = γ×adiabatic slope
adiabatic curve slope = γ× isothermal slope
adiabatic curve slope = (1/2) × isothermal curve slope
The correct Answer is:C
To find the relationship between the slopes of isothermal and adiabatic curves, we will analyze the equations governing these processes for an ideal gas.
1. Understand Isothermal Process:
- For an isothermal process (constant temperature), the ideal gas law can be expressed as:
PV=nRT(where T is constant)
- Rearranging gives:
PV=constant
- The slope of the isothermal curve can be derived by differentiating this equation.
2. Differentiate Isothermal Equation:
- From PV=constant, we can differentiate:
PdV+VdP=0
- Rearranging gives:
dP=−PVdV
- Thus, the slope dPdV for the isothermal process is:
dPdV=−PV(Equation 1)
3. Understand Adiabatic Process:
- For an adiabatic process, the relationship is given by:
PVγ=constant(where γ=CpCv)
- Differentiating this gives:
PdV+VγdP=0
- Rearranging gives:
dP=−PVγdV
- Thus, the slope dPdV for the adiabatic process is:
dPdV=−γPV(Equation 2)
4. Relate the Slopes:
- From Equations 1 and 2, we can see that:
dPdV (adiabatic)=γ×dPdV (isothermal)
- This shows that the slope of the adiabatic curve is γ times the slope of the isothermal curve.
5. Conclusion:
- Therefore, we conclude that:
Slope of adiabatic curve=γ×Slope of isothermal curve
Final Answer:
The slope of the adiabatic curve is related to the slope of the isothermal curve by the equation:
Slopeadiabatic=γ×Slopeisothermal
- For an isothermal process (constant temperature), the ideal gas law can be expressed as:
PV=nRT(where T is constant)
- Rearranging gives:
PV=constant
- The slope of the isothermal curve can be derived by differentiating this equation.
- From PV=constant, we can differentiate:
PdV+VdP=0
- Rearranging gives:
dP=−PVdV
- Thus, the slope dPdV for the isothermal process is:
dPdV=−PV(Equation 1)
- For an adiabatic process, the relationship is given by:
PVγ=constant(where γ=CpCv)
- Differentiating this gives:
PdV+VγdP=0
- Rearranging gives:
dP=−PVγdV
- Thus, the slope dPdV for the adiabatic process is:
dPdV=−γPV(Equation 2)
- From Equations 1 and 2, we can see that:
dPdV (adiabatic)=γ×dPdV (isothermal)
- This shows that the slope of the adiabatic curve is γ times the slope of the isothermal curve.
- Therefore, we conclude that:
Slope of adiabatic curve=γ×Slope of isothermal curve
The slope of the adiabatic curve is related to the slope of the isothermal curve by the equation:
Slopeadiabatic=γ×Slopeisothermal
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( MORE THAN ONE CORRECT CHOICE TYPE )9videos
THE FIRST LAW OF THERMODYNAMICS
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( LINKED COMPREHENSION )15videos
THE FIRST LAW OF THERMODYNAMICS
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PROBLEMS41videos
THE FIRST LAW OF THERMODYNAMICS
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - PRACTICE QUESTIONS72videos
THE KINETIC THEORY OF GASES
Similar Questions
Knowledge Check
- Question 1 - Select One
The relation between the slope of isothermal curve and slope of adiabatic curve is
Aslope of adiabatic curve =γ times slope of isothermal curveBslope of isothermal curve =γ times slope of adiabatic curveCslope of adiabatic curve =γ2 times slope of isothermal curveDslope of isothermal curve =γ2 times slope of adiabatic curve - Question 2 - Select One
The relation between the slope of isothemal curve and slope of adiabatic curve
Aslope of adiabatic curve =γ times slope of isotharmal curveBslope of isothermal curve =γ times slope of adiabatic curveCslope of adiabatic curve =γ2 times slope of isothermal curveDslope of isothermal curve =γ2 times slope of adiabatic curve - Question 3 - Select One
The slope of indicator curve in adiabatic change relative to volume axis is -
AP/VγB(Pγ/Vγ−1CPγ(V)D−γ(PV)
Reversible Isothermal and Adiabatic process
View SolutionComparison of Isothermal and Adiabatic work
View SolutionThe curves A and B in the figure shown P-V graphs for an isothermal and an adiabatic process for an idea gas. The isothermal process is represented by the curve A.
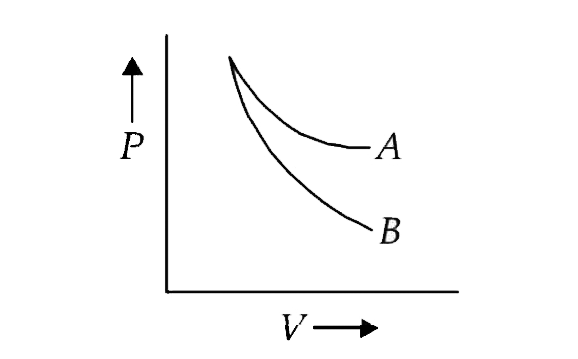 View Solution
View SolutionAnalysis OF Isothermal and Adiabatic Process
View SolutionA gas may expand either adiabatically or isothermally. A number of p−V curves are drawn for the two processes over different ranges of pressure and volume, it will be found that
(i) Two adiabatic curves do not intersect
(ii) two isothermal curves do not intersect
(iii) an adiabatic curve and an isothermal curve may intersect.
(iv) the magnitude of the slope of an adiabatic curve is greater thanthe magnitude of the slope of an isothermal curveView Solution

