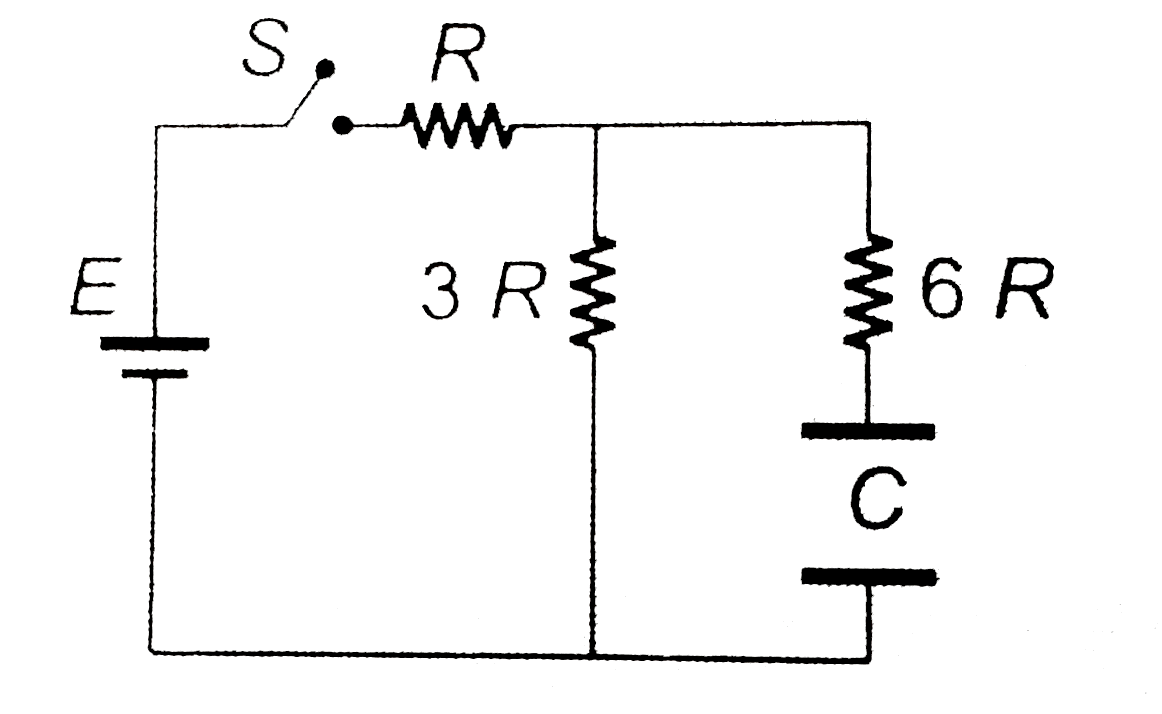
Find currents through resistors
(i) immediately after closing the switch
(ii) after a long time.
(a) At t=0 capacitor offers zero resistance i.e. it can be replaced by wire.
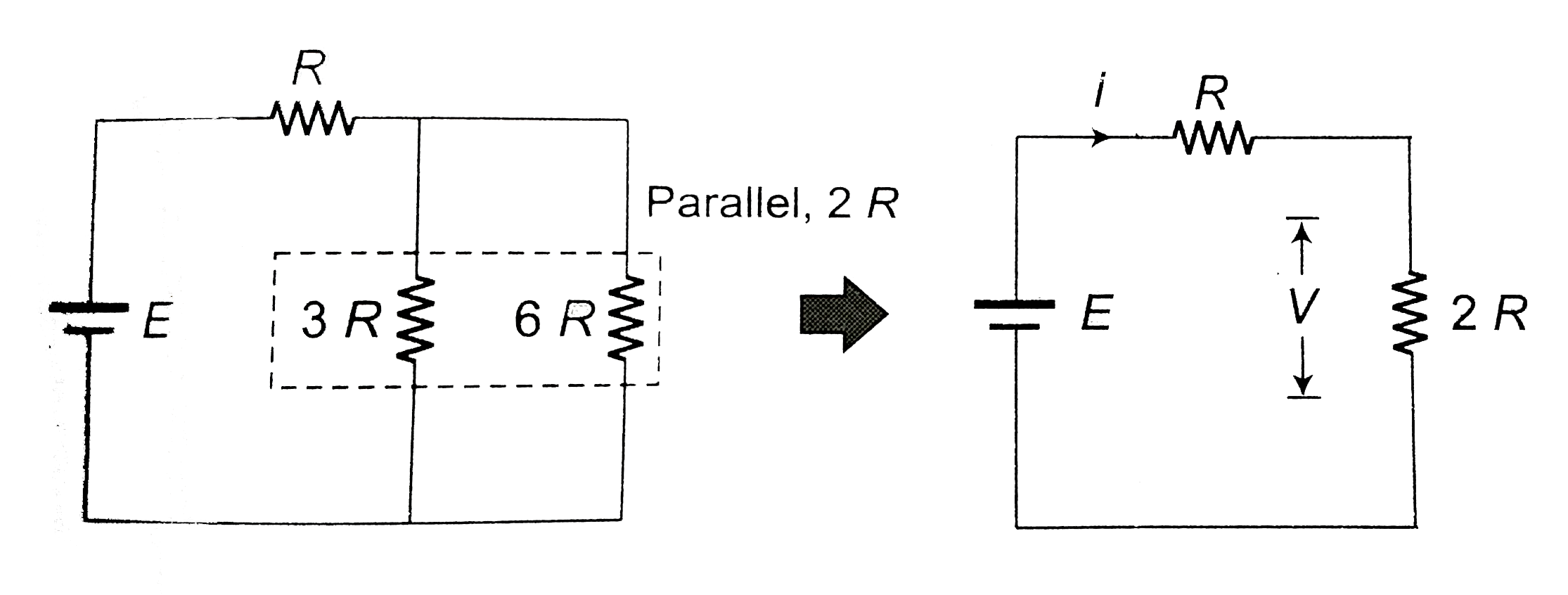
I=ER+2R=E3R
V=I×2R=2E3

i1=2E/33R=2E9R ltbr> i2=2E/36R=E9R
(b) After a long time i.e., t=∞, capacitor, offers infinte resistance. No current flows through the resistance in series with capacitor

i=ER+3R=E4R gt
Topper's Solved these Questions
- THERMAL AND ELECTRIC EFFECT oF CURRENTBOOK - CP SINGHCHAPTER - THERMAL AND ELECTRIC EFFECT oF CURRENTEXERCISE - Exercises
101 Videos
- SEMICONDUCTORSBOOK - CP SINGHCHAPTER - SEMICONDUCTORSEXERCISE - Exercises
140 Videos
- WAVE NATURE OF LIGHTBOOK - CP SINGHCHAPTER - WAVE NATURE OF LIGHTEXERCISE - EXERCISES
140 Videos
Similar Questions
Consider the circuits shown in figure. Find
(a)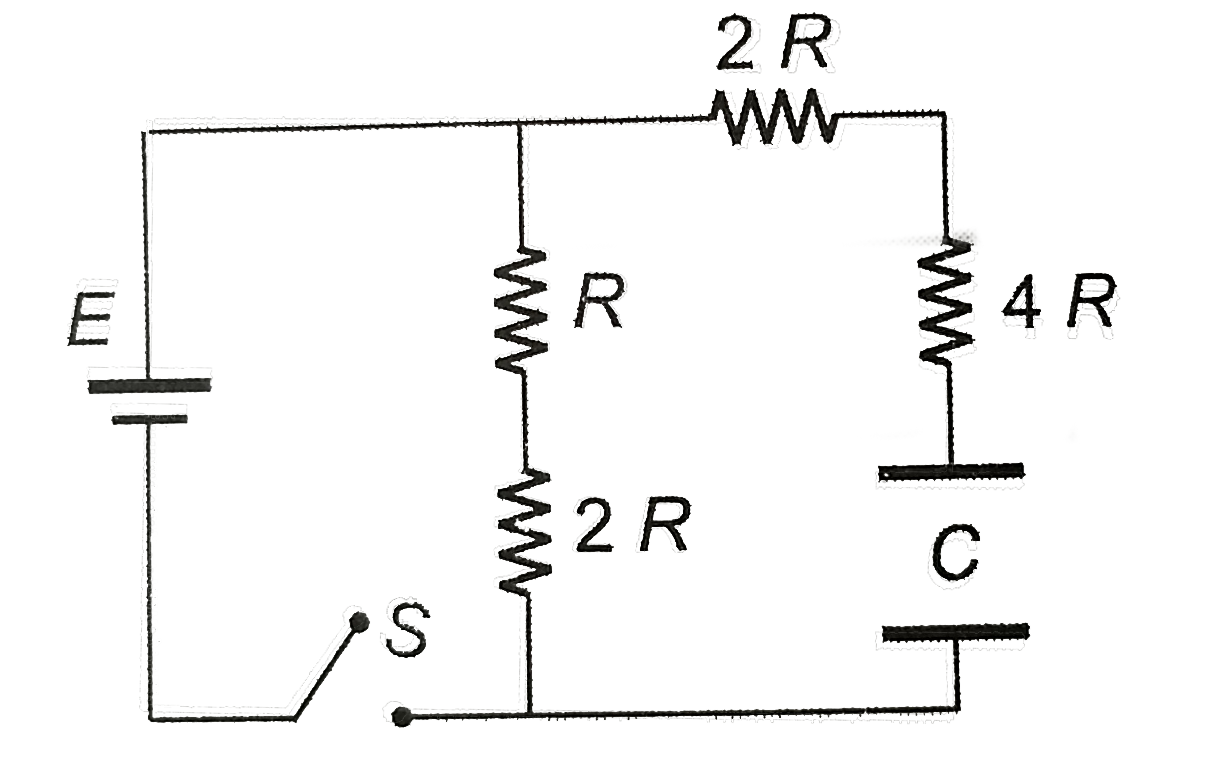
(b)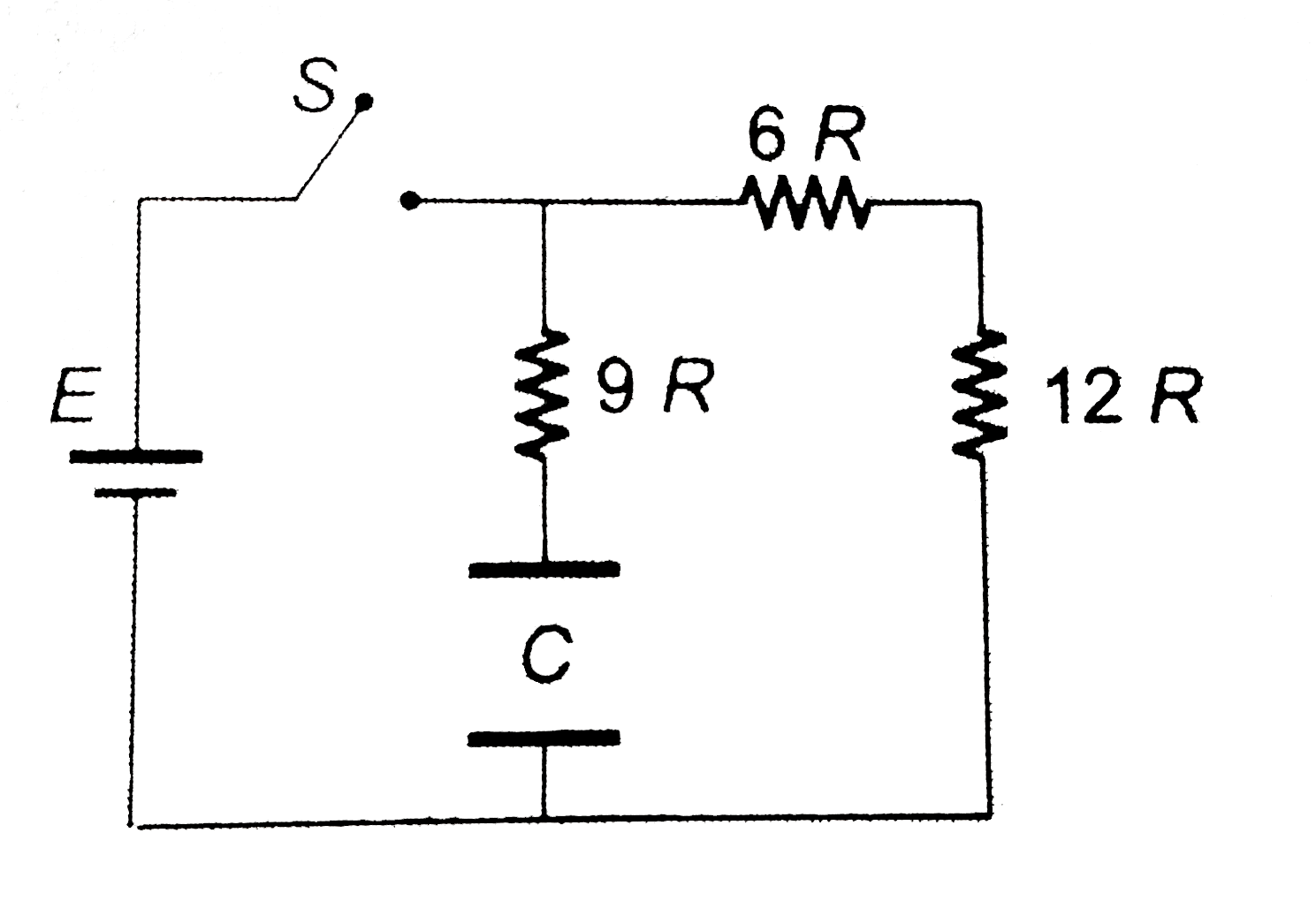
(c )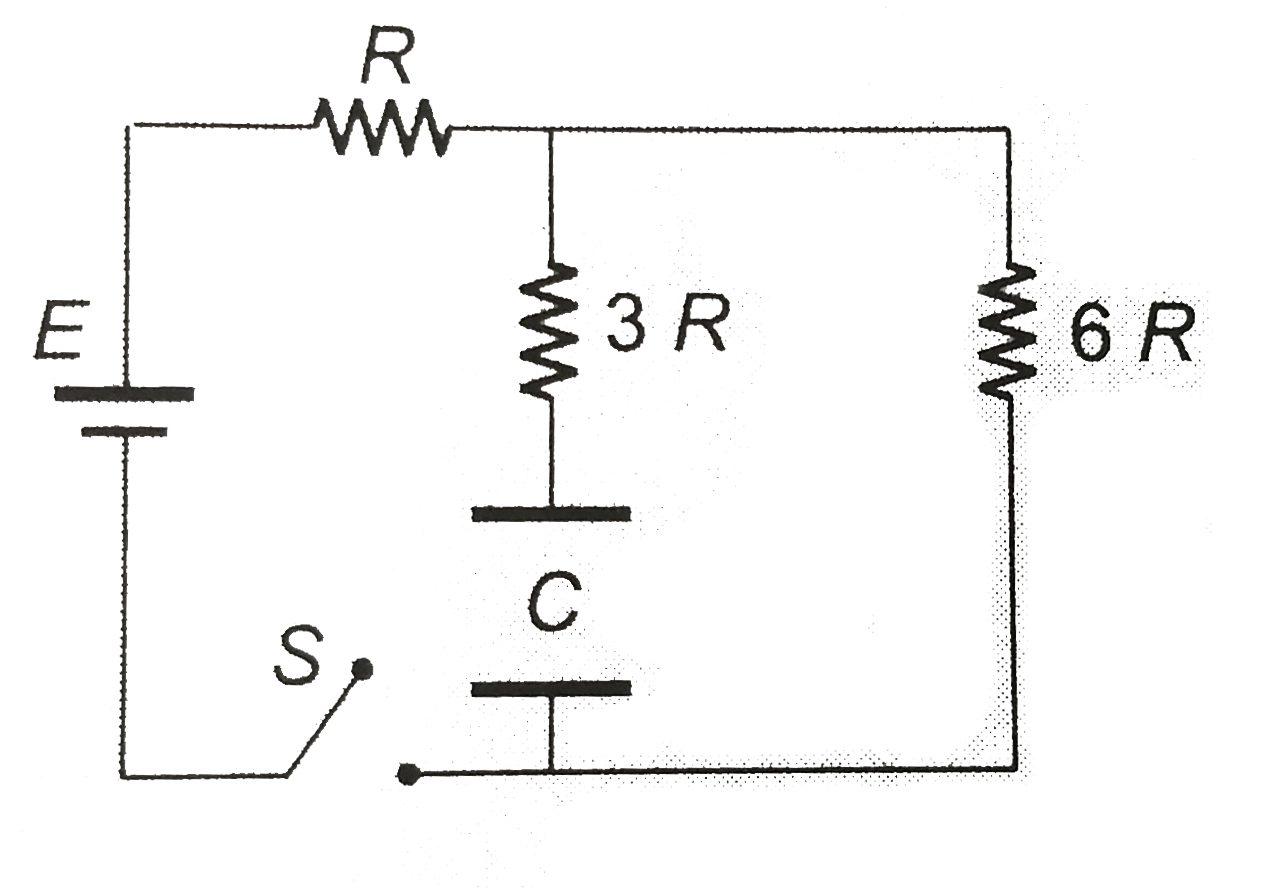
(d)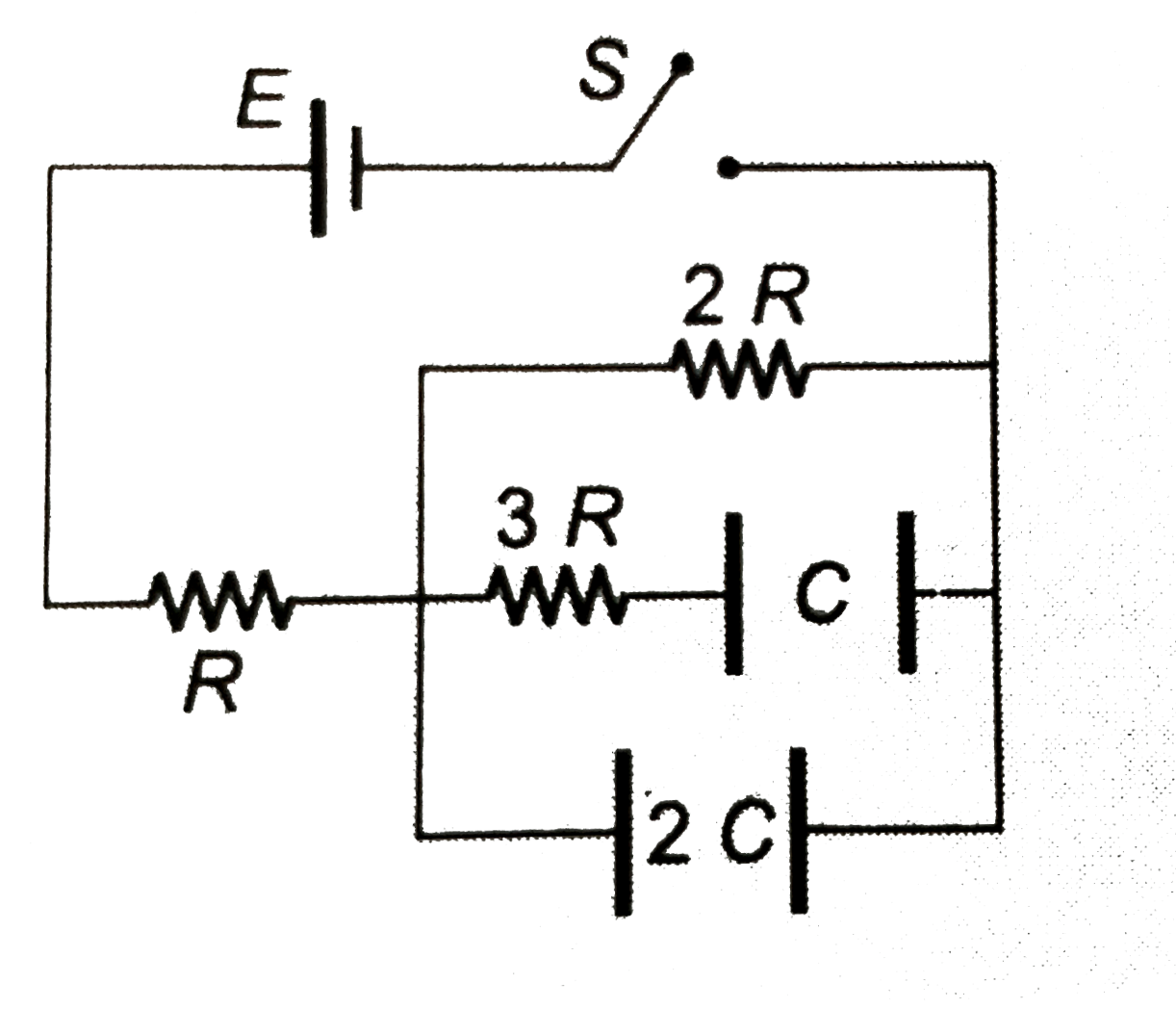
(i) currents through resistances immediately after closing the switch
(ii) Currents through resistaces after a long time ie., steady state.
View SolutionIn the circuit shown in figure, the current through each resistor is I. Find the currents through the resistors immediately after the switch ‘S’ is opened. How much heat will get dissipated in the circuit after thw switch is opened ?
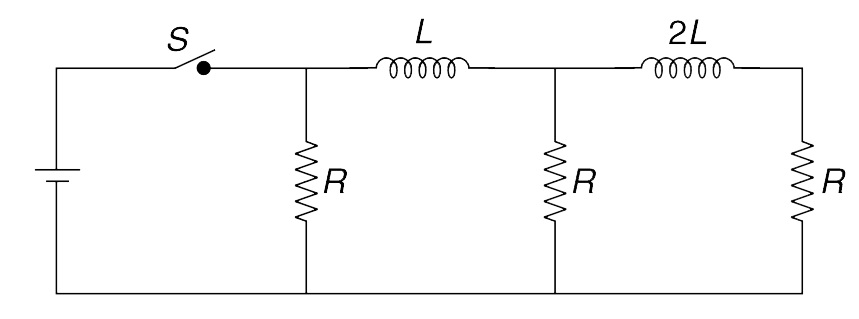
View Solution
Knowledge Check
A network of uncharged capacitors and resistances is as shown
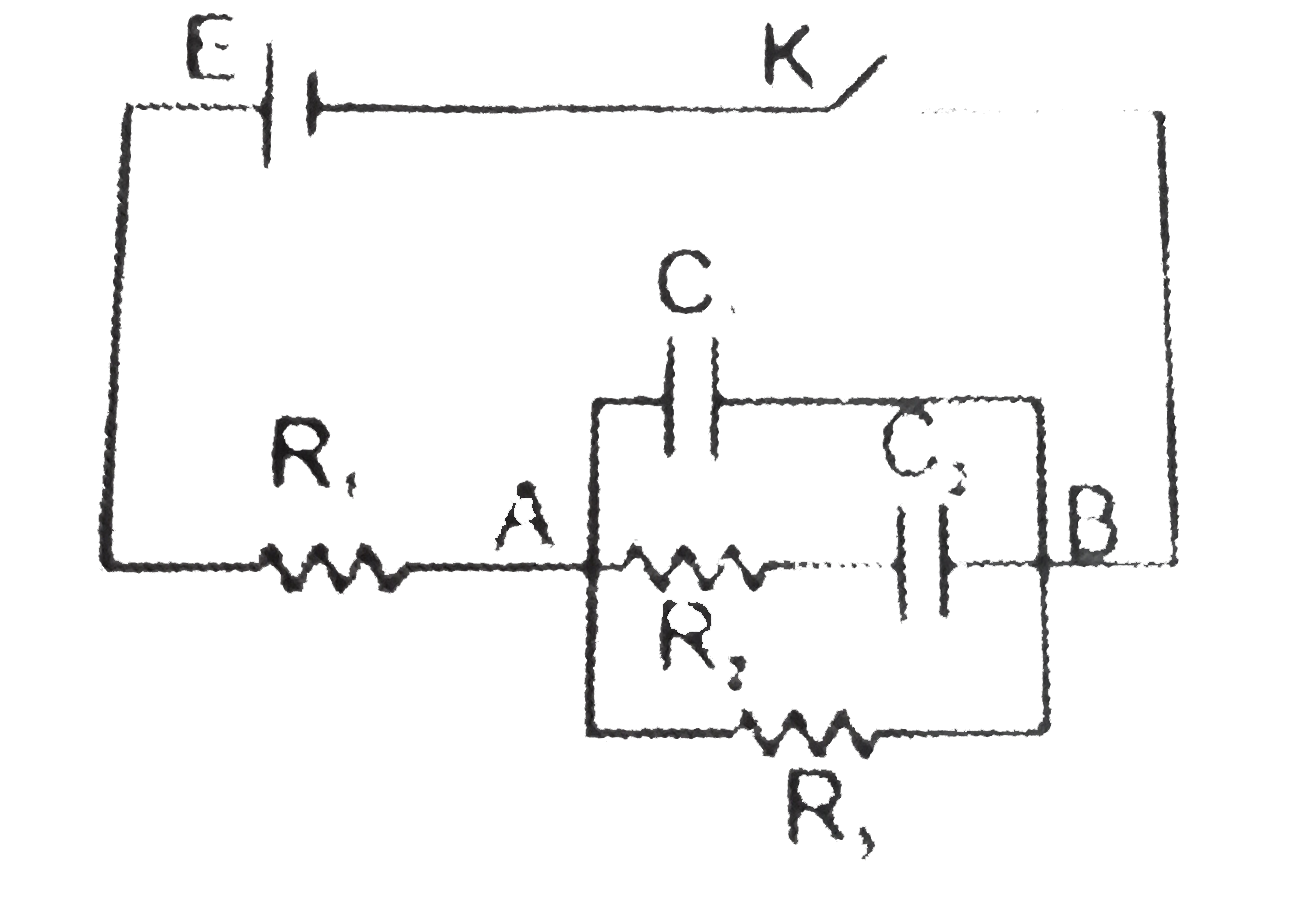
Current through the battery immediately after key K is closed and after a long time interval is :AER1,ER1+R3BER1+R3,ER1+R2R3R2+R3CZero, ER1DER1+R2R3R2+R3,ER1The figure shows three circuit with identical batteries, inductors, and resistors. Rank the circuit according to the current through the battery (i) just after the switch is closed and (ii) a long time later, greatest first
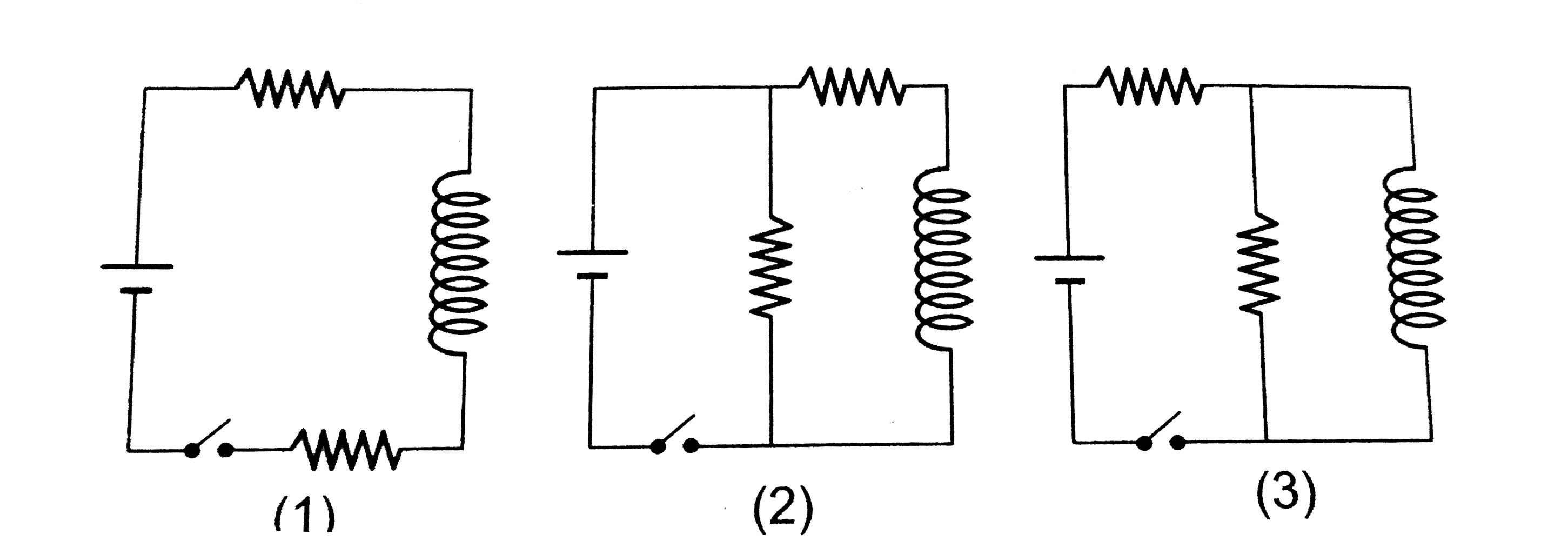 A(i)i2>i3>i1(i1=0)(ii)i2>i3>i1B(i)i2>i3>i1(i1≠0)(ii)i2>i3>i1C(i)i2=i3=i1(i1=0)(ii)i2>i3>i1D(i)i2=i3=i1(i1≠0)(ii)i2>i3>i1
A(i)i2>i3>i1(i1=0)(ii)i2>i3>i1B(i)i2>i3>i1(i1≠0)(ii)i2>i3>i1C(i)i2=i3=i1(i1=0)(ii)i2>i3>i1D(i)i2=i3=i1(i1≠0)(ii)i2>i3>i1
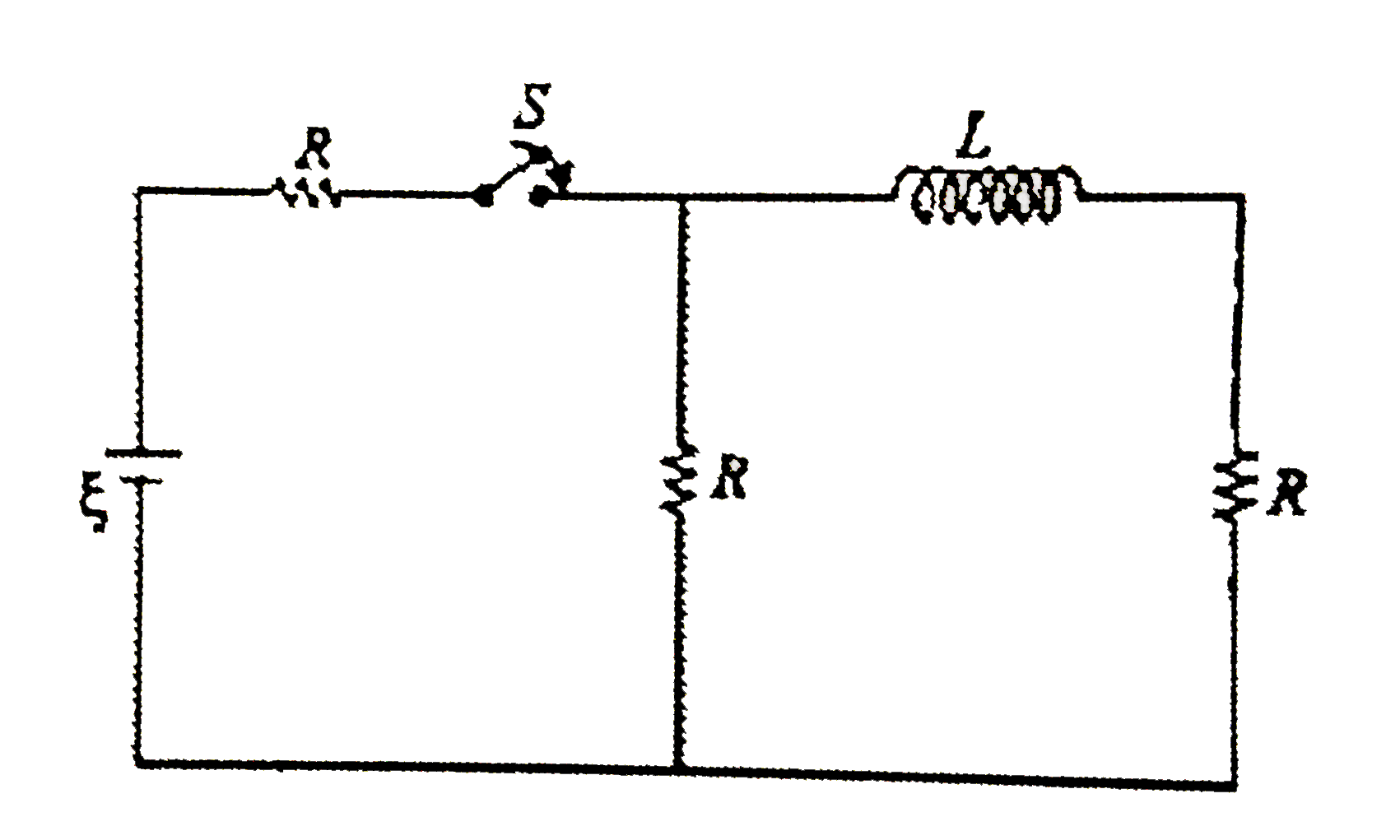
In cirucit shown in figure-5.111, find the current through battery just after closing the switch and after a long time in steady state.
View SolutionIn the connection shown in the figure the switch K is open and the capacitor is uncharged. Then we close the switch and let the capacitor charge up to the maximum and open the switch again. Then
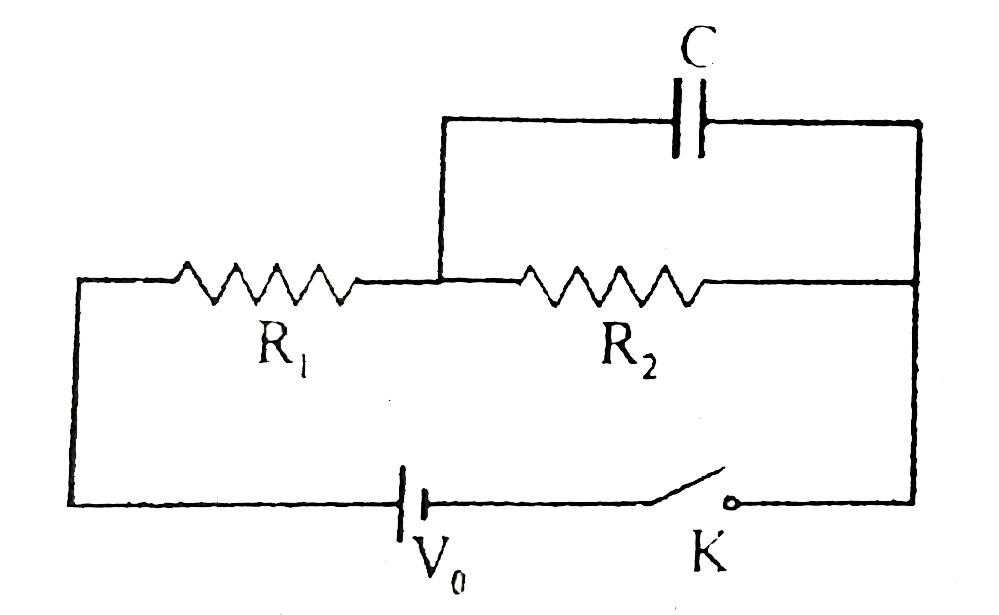
(a) the current through R1 be I1 immediately after closing the switch,
(b) the current through R2 be I3 immediately after reopening the switch, Find I1I2I3 (in ampere−1) (Use the following data: V0=30VR1=10KΩR2=5kΩ)
View SolutionDetermine the current through the battery in the circuit shown in figure.
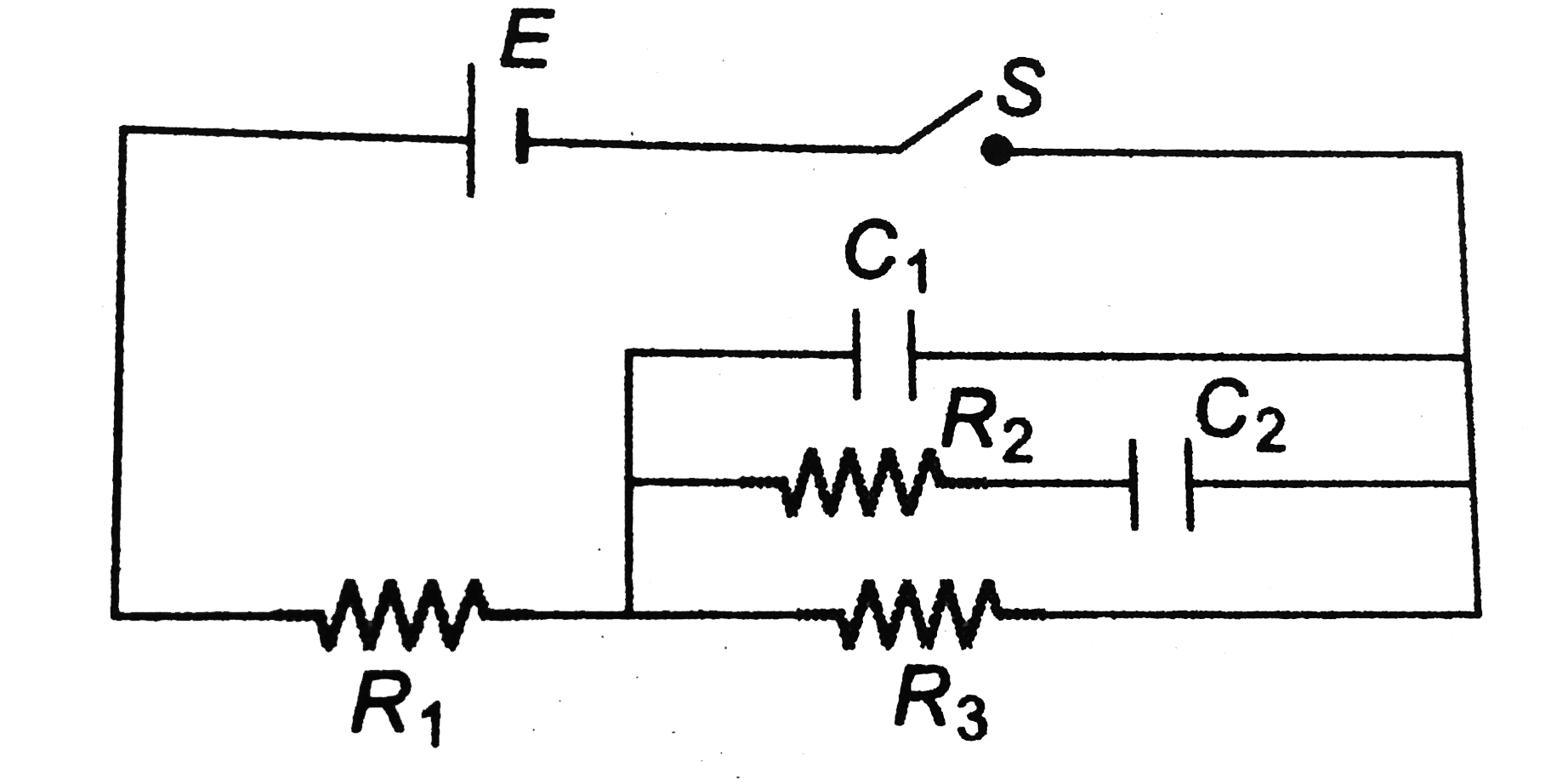
(a) immediately after the switch S is closed
(b) after a long time.
View SolutionAt t=0 switch S1 is closed and remains closed for a long time and S2 remains open. Now S1 is opened and S2 is closed. Find out
(i) The current through the capacitor immediately after that moment
(ii) Charge on the capacitor long after that moment.
(iii) Total charge flown through the cell of emf 2ε after S2 is closed.
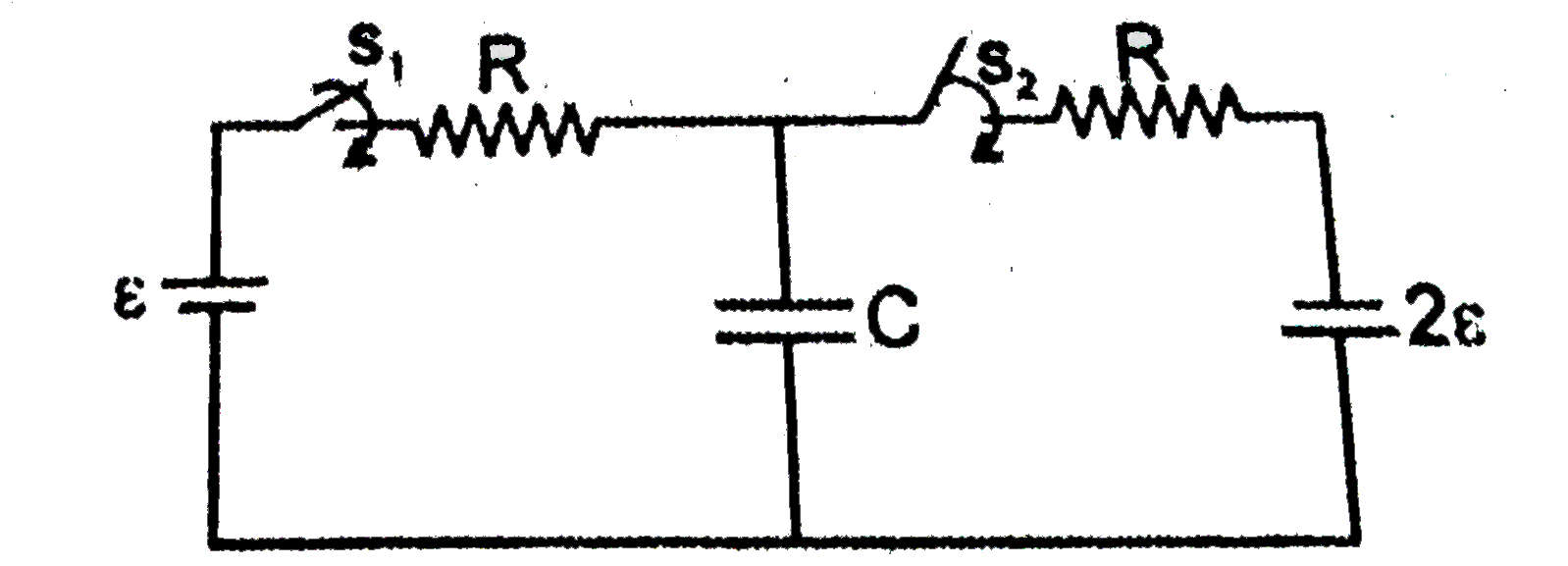
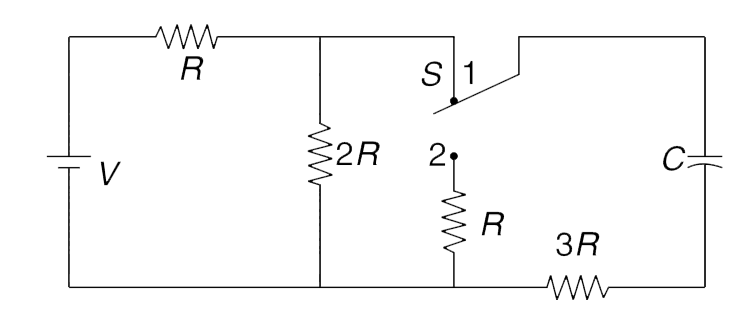
View SolutionConsider the circuit shown in the figure. The switch has been in position 1 for a long time. Answer following questions:
(a) find current through 2R.
(b) find potential difference across the capacitor.
(c) At t=0 the switch is moved to position 2. What current flows through the capacitor immediately after the switch is placed to position 2?
(d) Draw a graph of current Vs time for the current through the capacitor after the switch is moved to position 2. Indicate the time on the graph when the current becomes 37% of its value immediately after the switch is put to position 2.
View SolutionFind the current through the battery
(i) just after the switch is closed.
(ii) long after the switch has been closed.
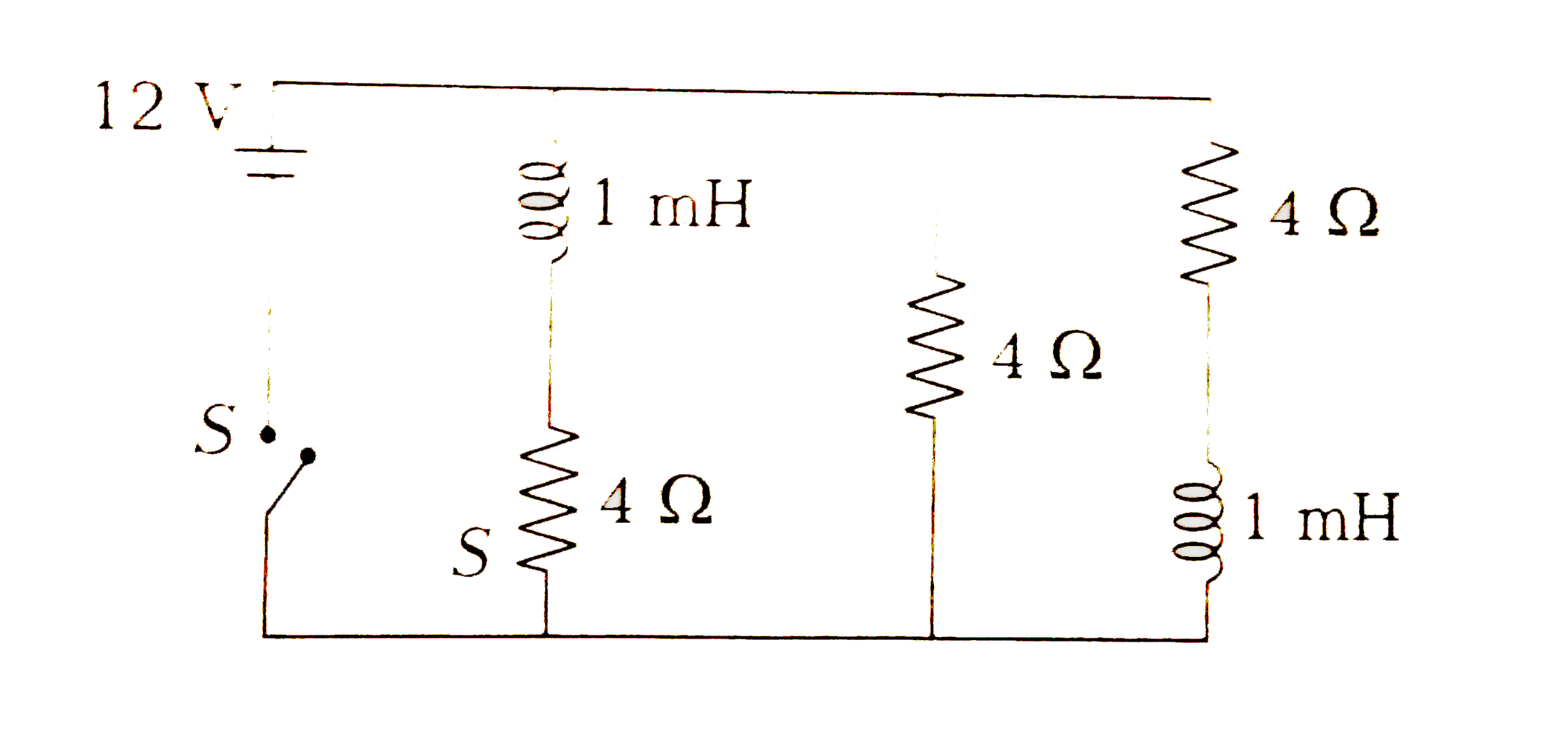
View Solution
