At t=0 switch S is closed .
(a) After how much time , charge on capacitor is 50% of maximum charge stored on capacitor.
(b) After how much time, energy stored in capacitor is halt of maximum energy stored in capacitor.
Video Solution
Text Solution
(a) q=CE(1−e−t/RC)
qmax=CE,q=qmax2=12CE
11CE=CE(1−e−t/RC)
e−t/RC=2
tRClog_(e) e = log_(e) 2 = 0.693RC<br>(b)U =(q^2)/(2C) = 1/2 CE^(2)(1-e^(-t//RC))^(2)<br>U_(max) = 1/2 CE^2, U = (U_(max))/(2) = (CE^2)/(4)<br>(CE^2)/(4) = (CE^2)/() (1-e^(-t//RC))^(2)<br>(1-e^(-t//RC))^(2) = 1/2 implies (1-e^(-t//RC))=1/(sqrt(2))<br>e^(-t//RC)=1-1/(sqrt(2)) = (sqrt(2)-1)/(sqrt(2))<br>e^(-t//RC) = (sqrt(2))/(sqrt(2)-1) = (sqrt(2))/(sqrt(2)-1)* ((sqrt(2)-1))/((sqrt(2)+1)) = (2+sqrt(2))<br>t/(RC ) log_(e) e = log_(e) (2+sqrt(2))<br.t = RC log_(e) (2+sqrt(2)).
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CP SINGHCHAPTER - THERMAL AND ELECTRIC EFFECT oF CURRENTEXERCISE - Exercises101videos
THERMAL AND ELECTRIC EFFECT oF CURRENT
- BOOK - CP SINGHCHAPTER - SEMICONDUCTORSEXERCISE - Exercises140videos
SEMICONDUCTORS
- BOOK - CP SINGHCHAPTER - WAVE NATURE OF LIGHTEXERCISE - EXERCISES140videos
WAVE NATURE OF LIGHT
Similar Questions
Knowledge Check
- Question 1 - Select One
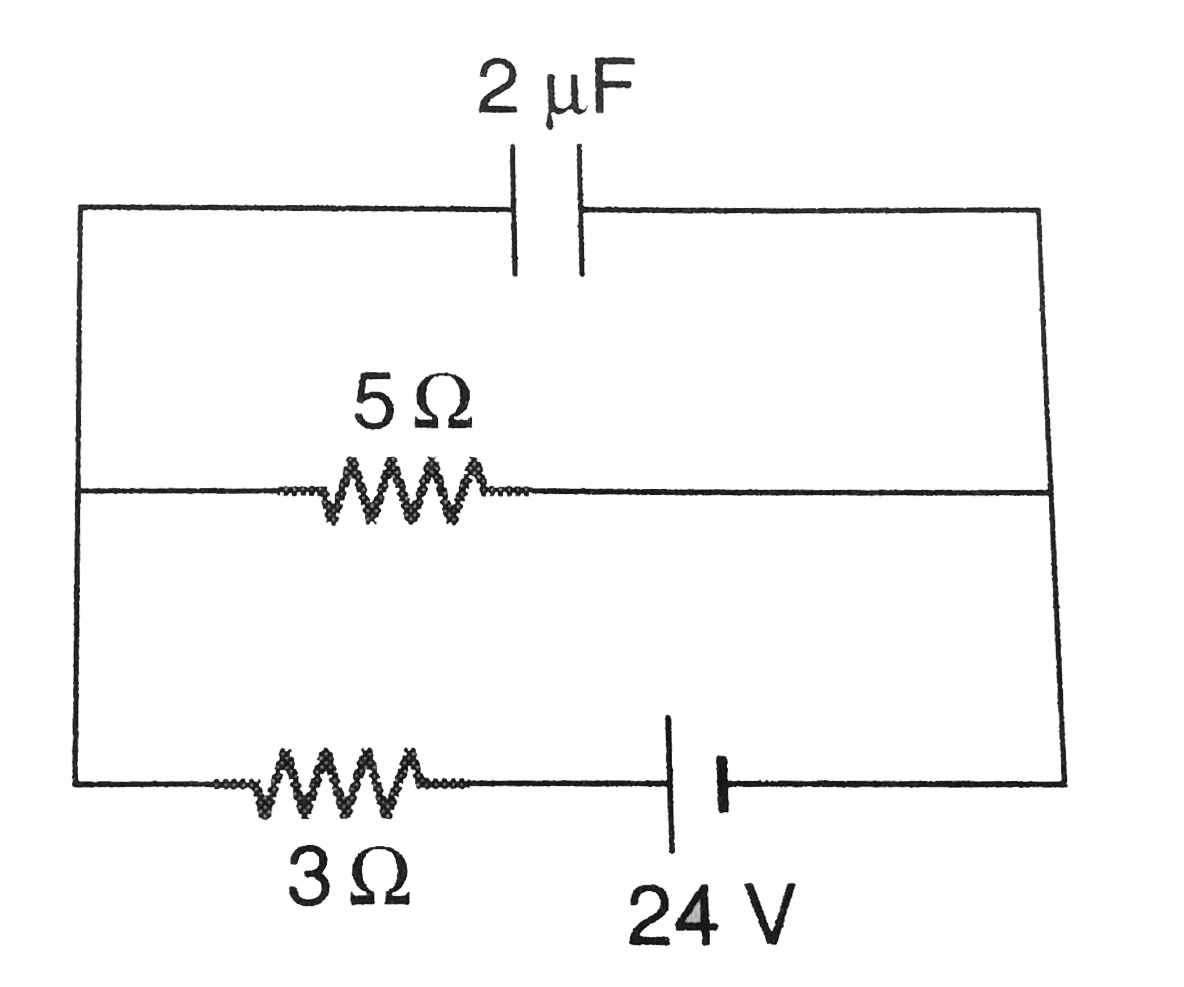
the energy stored in the capacitor isA12μJB24μJC36μJD48μJ - Question 2 - Select One
Energy Stored in the capacitor is
Aε0E2×AdB(12)ε0E2×AdCε0E2×AdDε0E×Ad - Question 3 - Select One
In a charged capacitor, the energy is stored in
Athe negative chargesBthe positive chargesCthe field between the platesDboth 'a' and 'b'
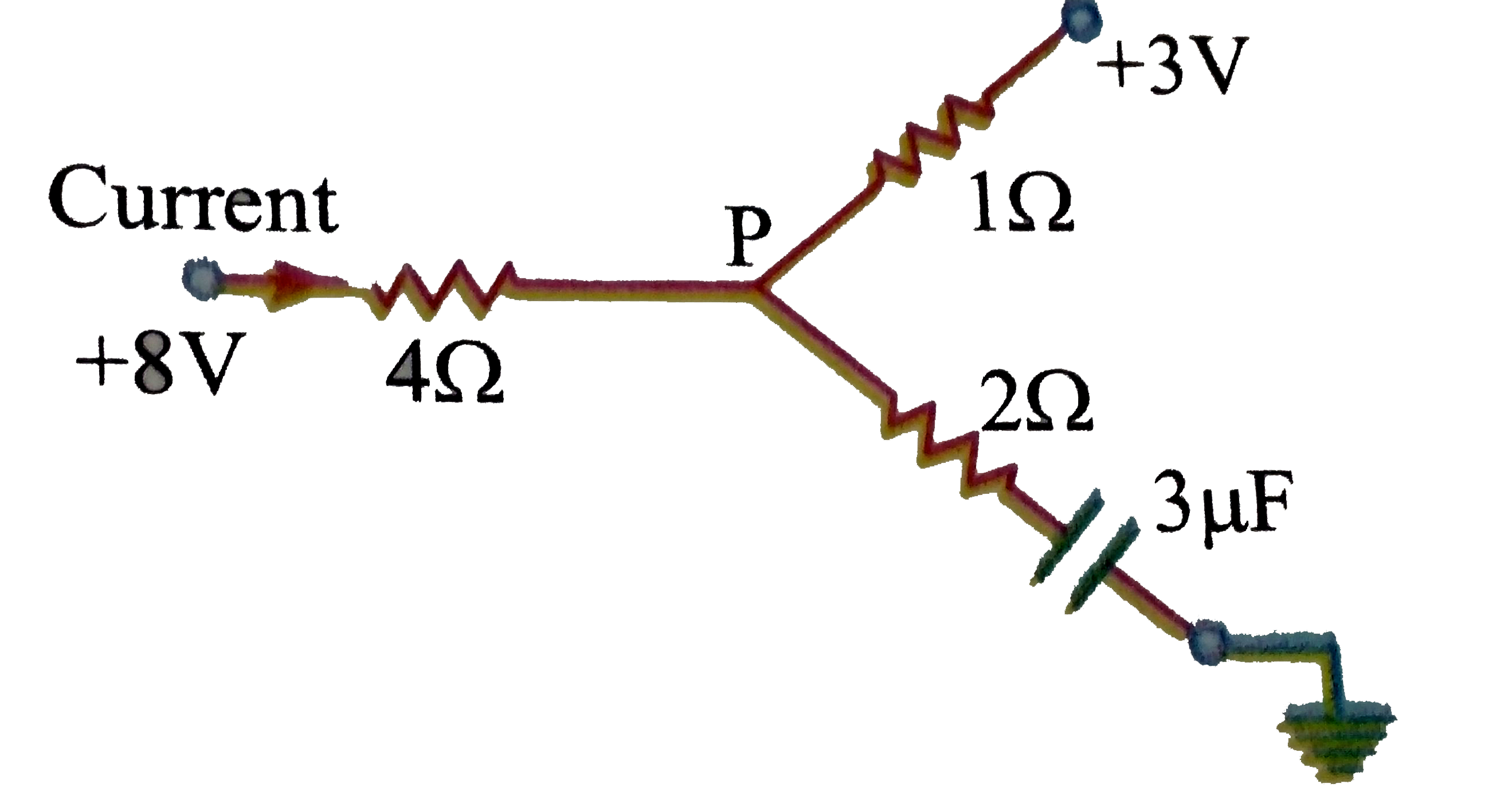
Find the charge stored in the capacitor.
 View Solution
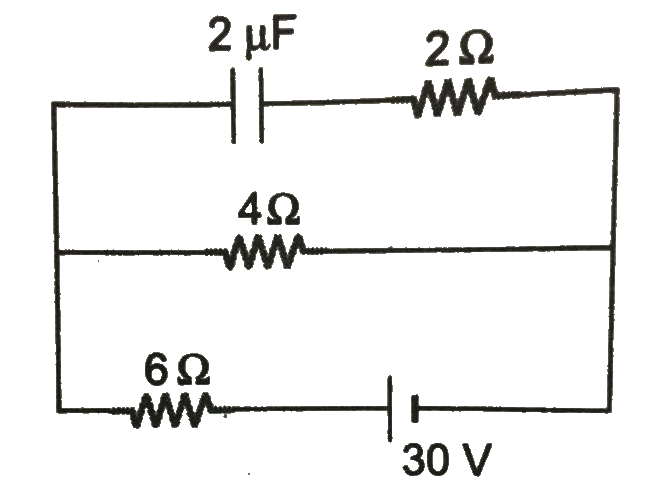
View SolutionFind the charge stored in the capacitor.
 View Solution
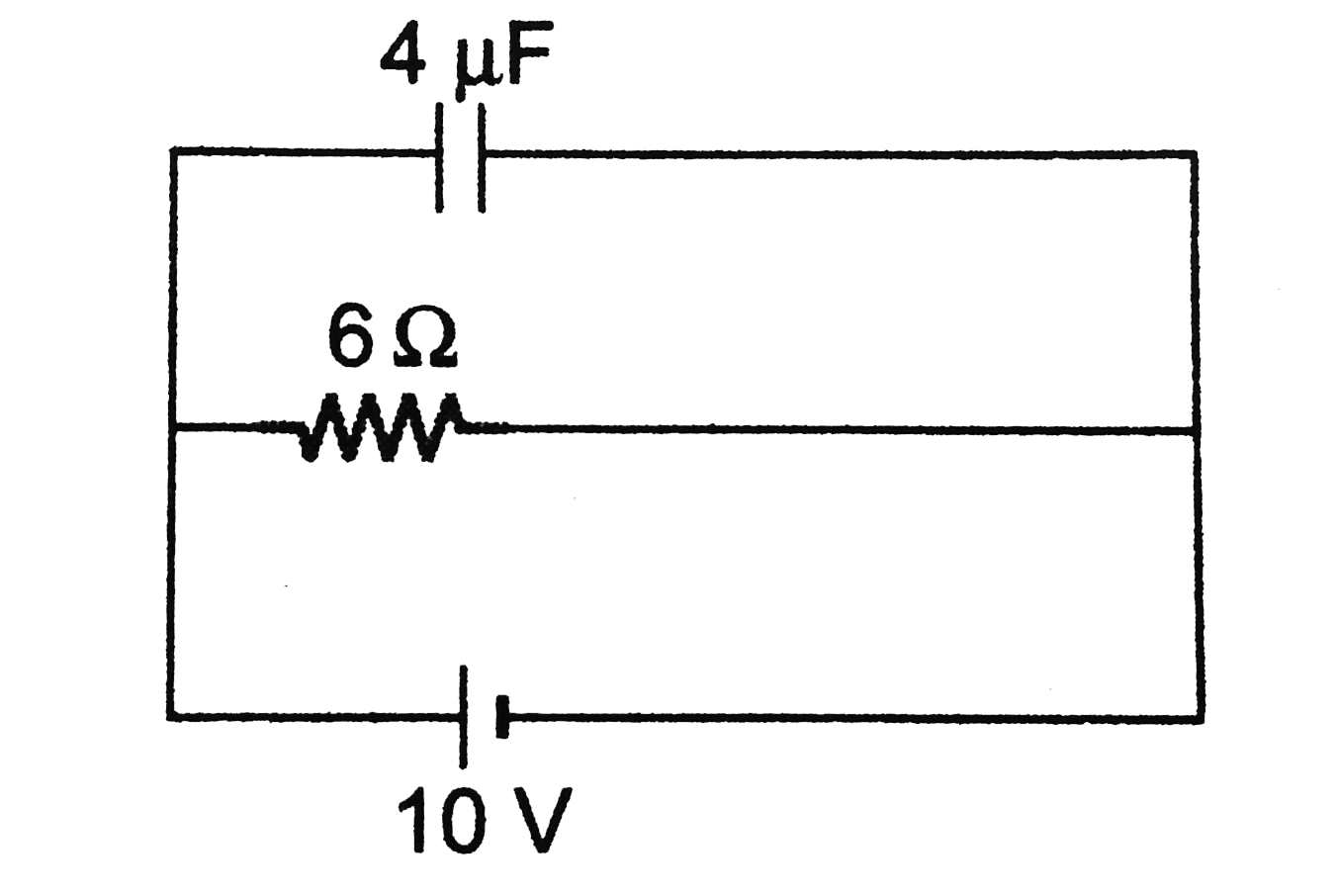
View Solution(a) Find charge on capacitors

(b) Find charge on capacitor
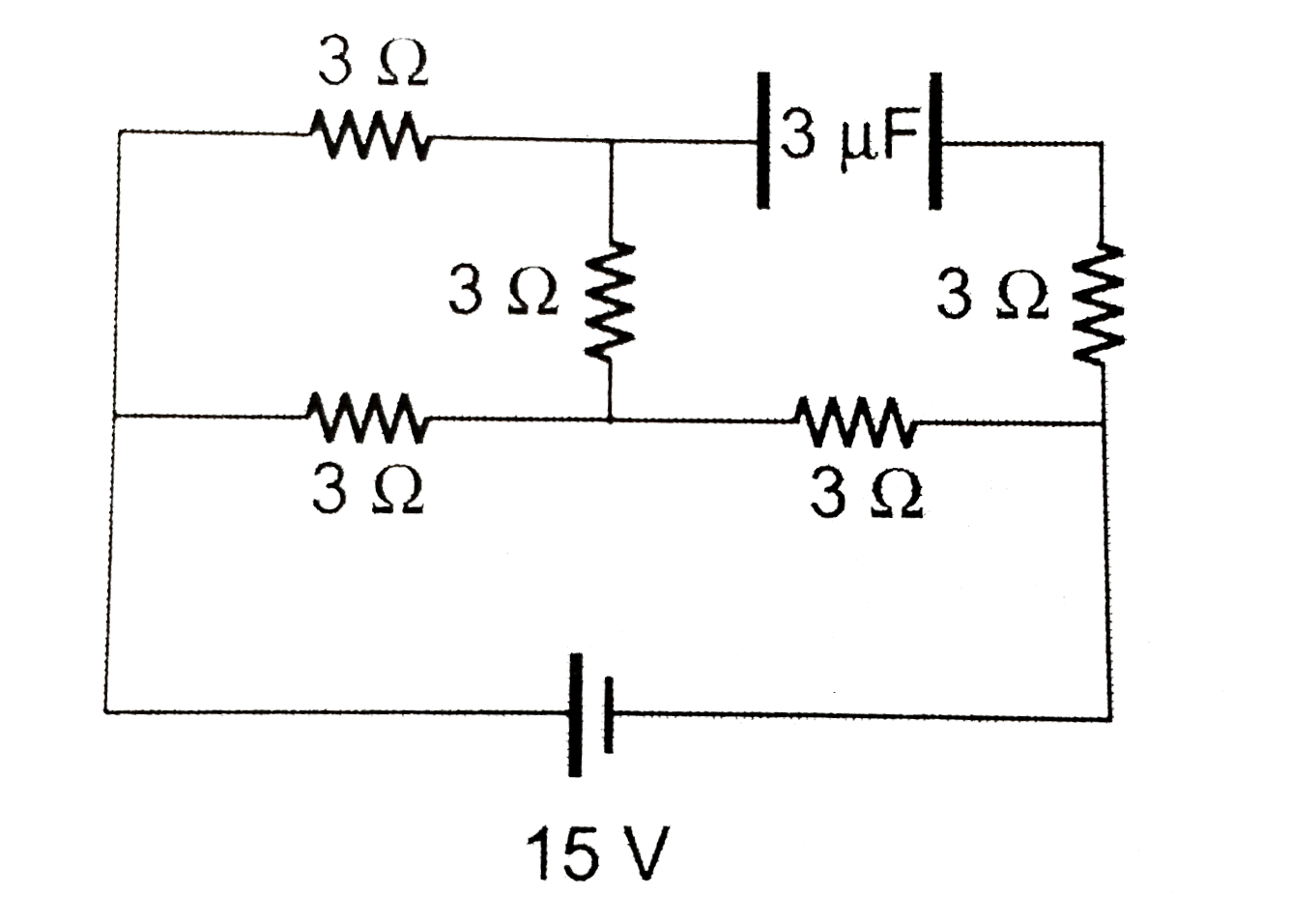
(c ) Find energy stored in capacitor.
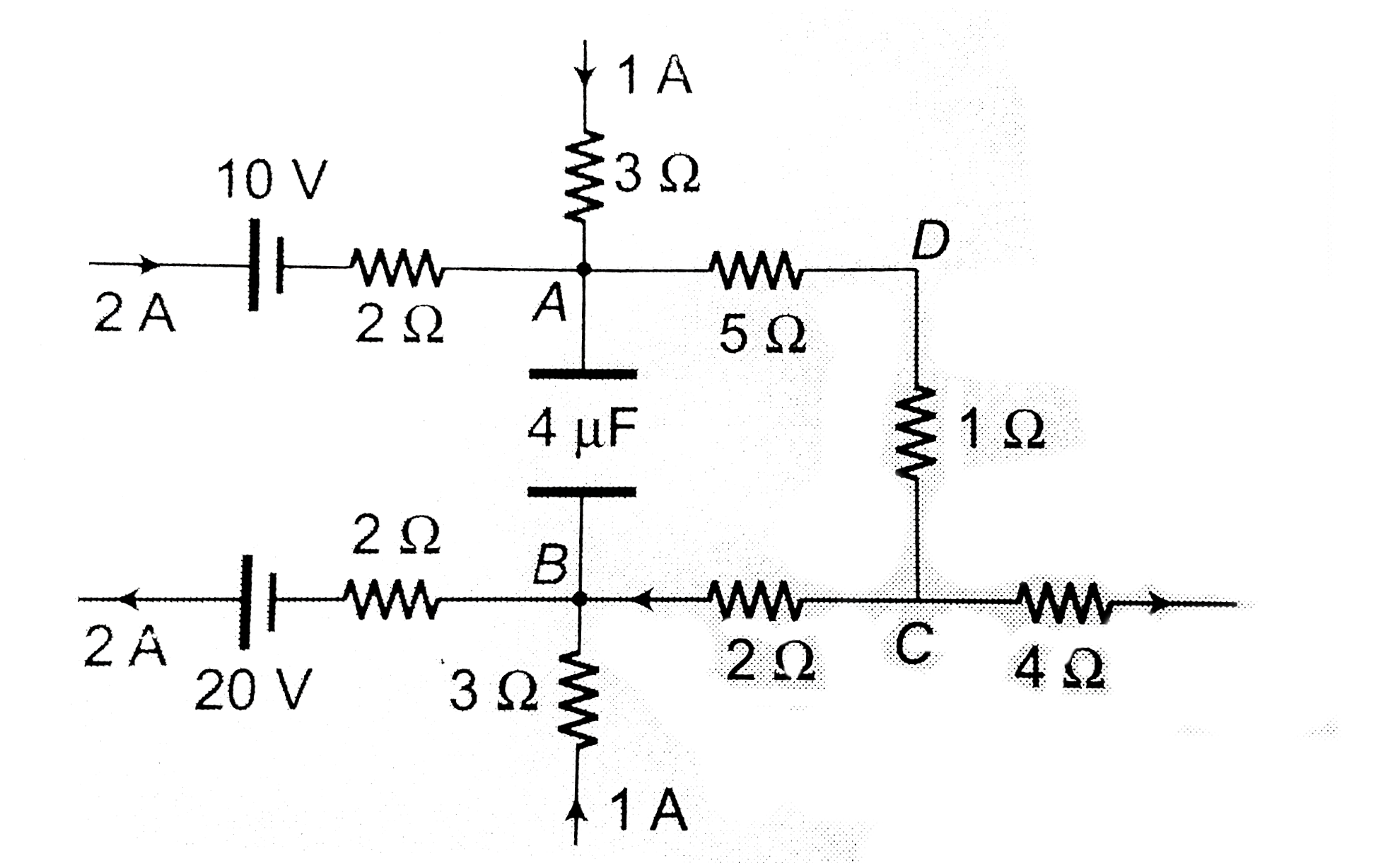 View Solution
View SolutionIf a 4μF capacitor is charged to 1 kV, then energy stored in the capacitor is
View SolutionIn a charged capacitor the energy is stored in
View Solution