An em wave going through vacuum is described by E=E0sin(kx−ωt)
B=B0sin(kx−ωt)
E0K=B0ω
E0=B0ωk
E0ω=B0k
none of these
The correct Answer is:A
E0=cB0=ωkB0
Topper's Solved these Questions
Similar Questions
A plane EM wave travelling along z direction is described by
E=E0sin(kz−ωt)ˆiandB=B0sin(kz−ωt)ˆj.
show that
(i) The average energy density of the wave is given by uav=14ε0E20+14B20μ0.
(ii) The time averaged intensity of the wave is given by Iav=12cε0E20.
View SolutionThe electric field of an electromagnetic wave travelling through vaccum is given by the equation E=E0sin(kx−ωt) The quantity that is independent of wavelength is
View Solution
Knowledge Check
An electromagnetic wave going through vacuum is described by
E=E0sin(kx−ωt),B=B0sin(kx−ωt).
ThenA(E0)k=(B0)ωB(E0)(B0)=ωkC(E0)ω=B0kDnone of these .An electromagnetic wave going through vacuum is described by →E=E0sin(kx−wt)and→B=B0sin(kx−wt). Which of the following equation is true?
AE0k=B0ωBE0ω=B0kCE0B0=ωkDE0ωk=B0An em wave going through vacuum is described by E=E0sin(kx−ωt)
B=B0sin(kx−ωt)AEok=B0ωBE0B0=ωkCE0ω=B0kDE0B0=ωk
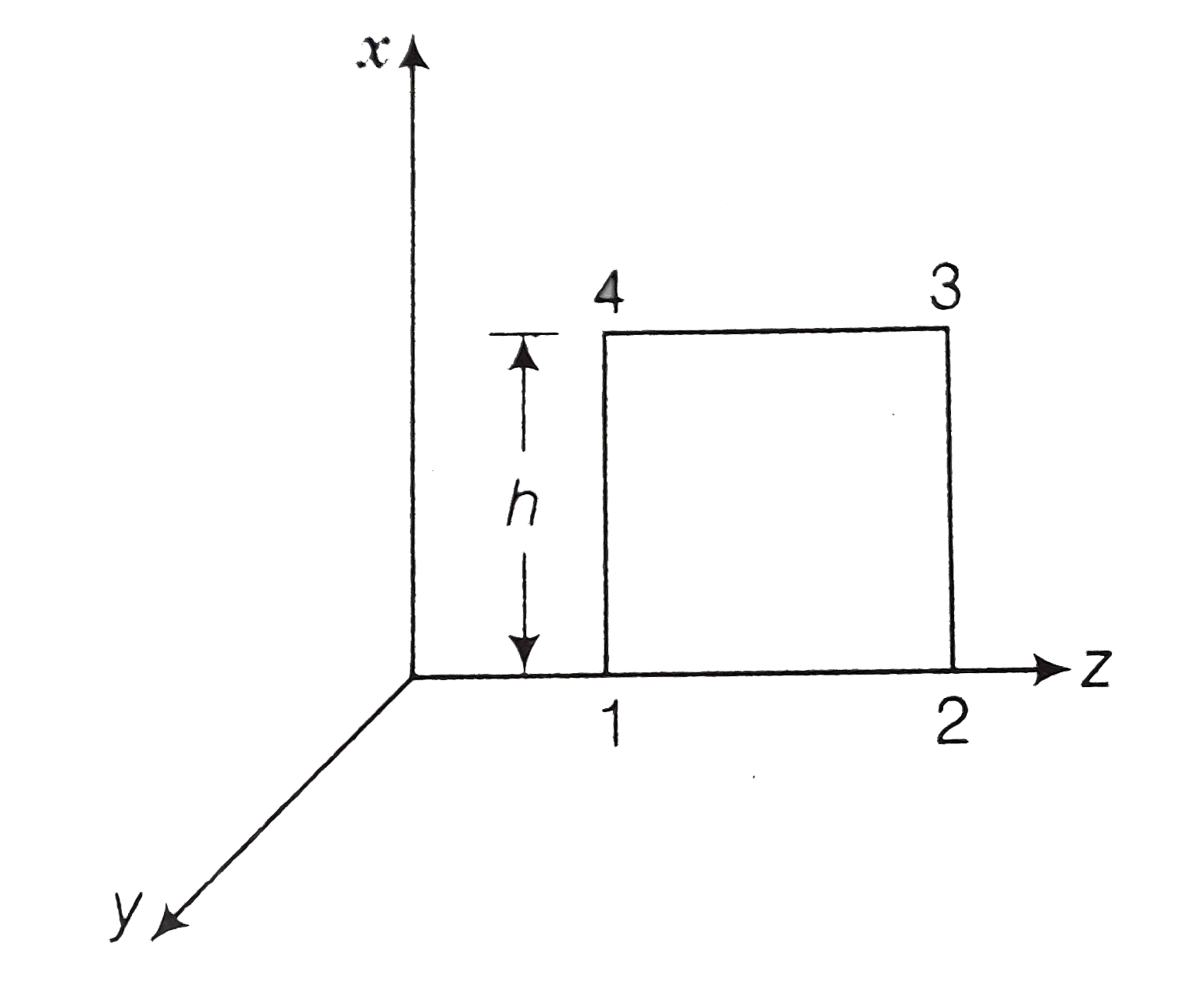
A plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
View SolutionAn electromagnetic wave going through vacuum is described by
E= E_0 sin(kx- omega t). Which of the following is/are independent of the wavelength?
View SolutionAn e.m. wave going through vacuum is denoted by E=E0sin(kx−ωt). Which of the following is /are independent of wavelength?
View SolutionA electromagnetic wave going through a medium is given by E=E0sin(kx–ωt)andB=B0sin(kx–ωt) then
View SolutionAn electromagneti wave propagationg through vacuum is given B=B0sin(kx−ω) . Which of the following is/are independent of frequency?
View Solution