The particle is moving such that its displacement along x-axis as a function of time is given by $x (x - 6) = 1 - 10 cos ω t$ . Find amplitude, time period and mean position.

Video Solution

Text Solution

Verified by Experts

$x (x - 6) = 1 - 10 cos ω t$ By adding $9$ on both sides
$x^{2} - 6 x + 9 = 10 - 10 cos ω t$
${(x - 3)}^{2} = 10 [1 - cos ω t] = 5 [{sin}^{2} (\frac{ω t}{2})]$
$(x - 3) = \sqrt{5} sin (\frac{ω t}{2})$
So motion of particle is $S H M$ with $A = \sqrt{5}$ units,
$T = \frac{4 π}{ω}$ units & means position is at $x = 3$ units.

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A point moves such that its displacement as a function of times is given by $x^{2} = t^{2} + 1$ . Its acceleration at time t is
A $\frac{1}{x^{3}}$
B $- \frac{1}{x^{2}}$
C $\frac{1}{x} - \frac{t^{2}}{x^{3}}$
D $\frac{1}{x} - \frac{t}{x^{3}}$
Question 2 - Select One
The displacement $x$ of a particle in motion is given in terms of time by $x (x - 4) = 1 - 5 cos ω t$
Athe particle executes $S H M$
Bthe particle executes oscillatory motion which is not $S H M$
Cthe motion of the particle is neither oscillatory nor simple harmonic
Dthe particle is not acted upon by a fprce when it is at $x = 4$
Question 3 - Select One
Figure shows the position of a particle moving on the x - axis as a function of time

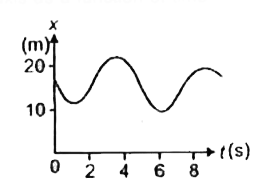AThe particle has come to rest 4 times
BThe velocity at t = 8 s is negative
CThe velocity remains positive for t = 2 s to t = 6 s
DThe particle moves with constant velocity.

NARAYNA-OSCILLATIONS-EXERCISE - IV

Home
Ask Doubt
Profile