A particle performing simple harmonic motion having time period 3 s is in phase with another particle which also undergoes simple harmonic motion at t=0. The time period of second particle is T (less that 3s). If they are again in the same phase for the third time after 45 s, then the value of T will be
A
2.8 s
B
2.7s
C
2.5s
D
3.2s
Video Solution
Text Solution
The correct Answer is:C
Δϕ=(2πT2−2πT1)Δt
After Δt=45s, they are again in phase for the 3rd time
Δϕ=3×2π=6π
6π=(2πT−2π3)(45)⇒T=2.5
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A particle undergoes simple harmonic motion having time period T. The time taken in 3/8th oscillation is
A38TB58TC512TD712TA particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2If particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
AZeroBT/2C2TDInfinite
The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=23s is
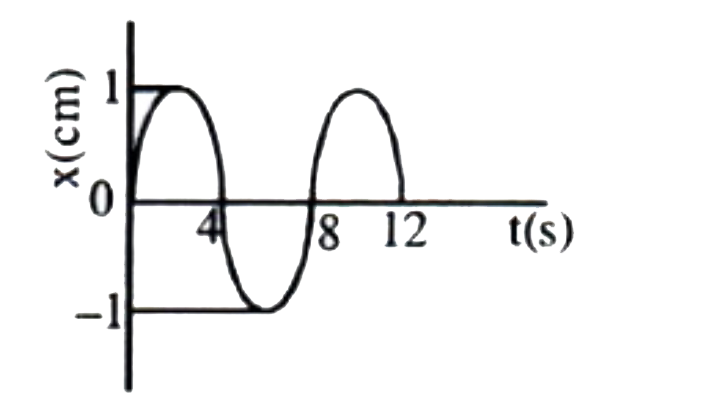
View SolutionThe phase (at a time t) of a particle in simple harmonic motion tells
View SolutionThe phase of a particle executing simple harmonic motion is π2 when it has
View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of t=4/3s is
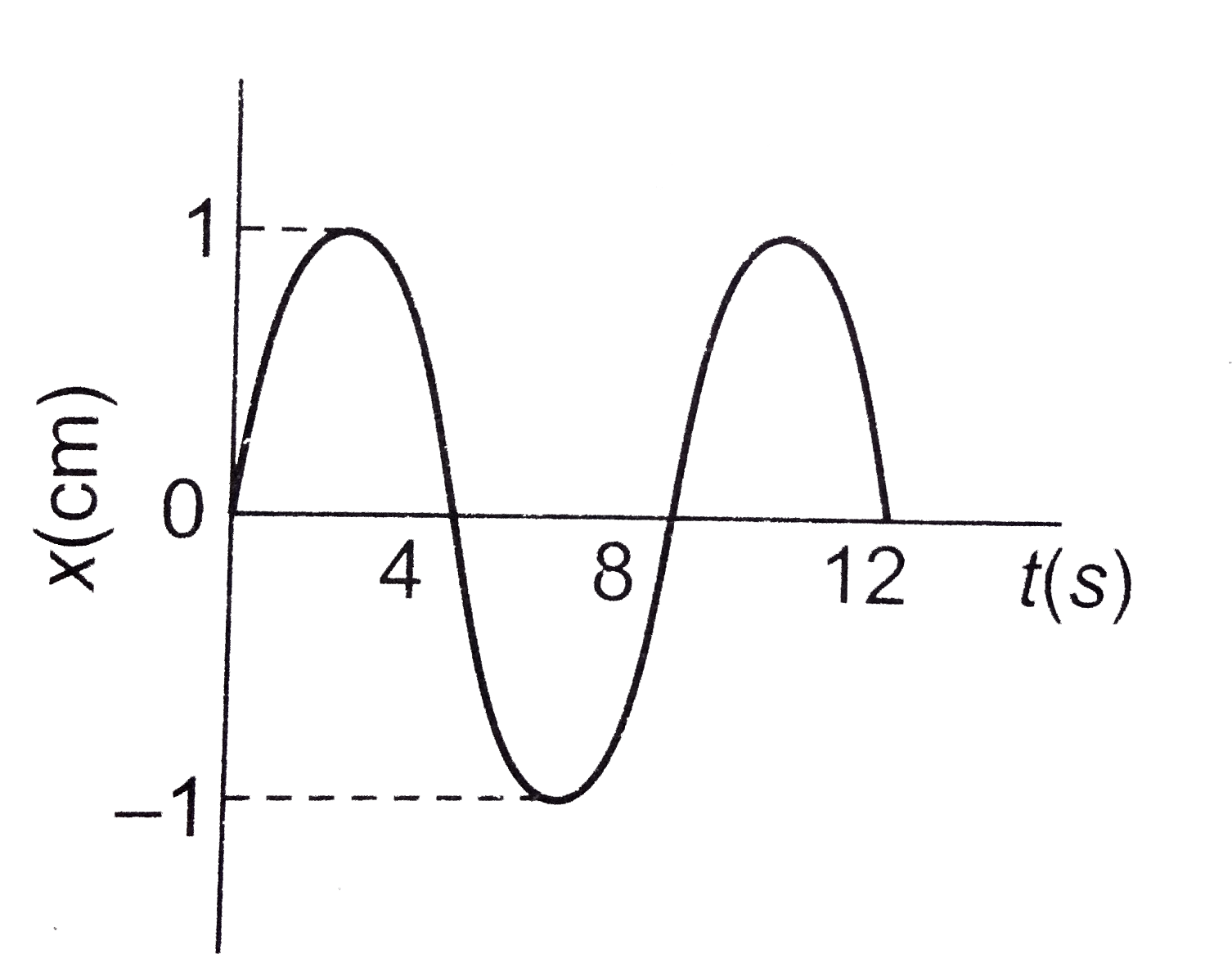
View SolutionThe x−t graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at t=4/3s is
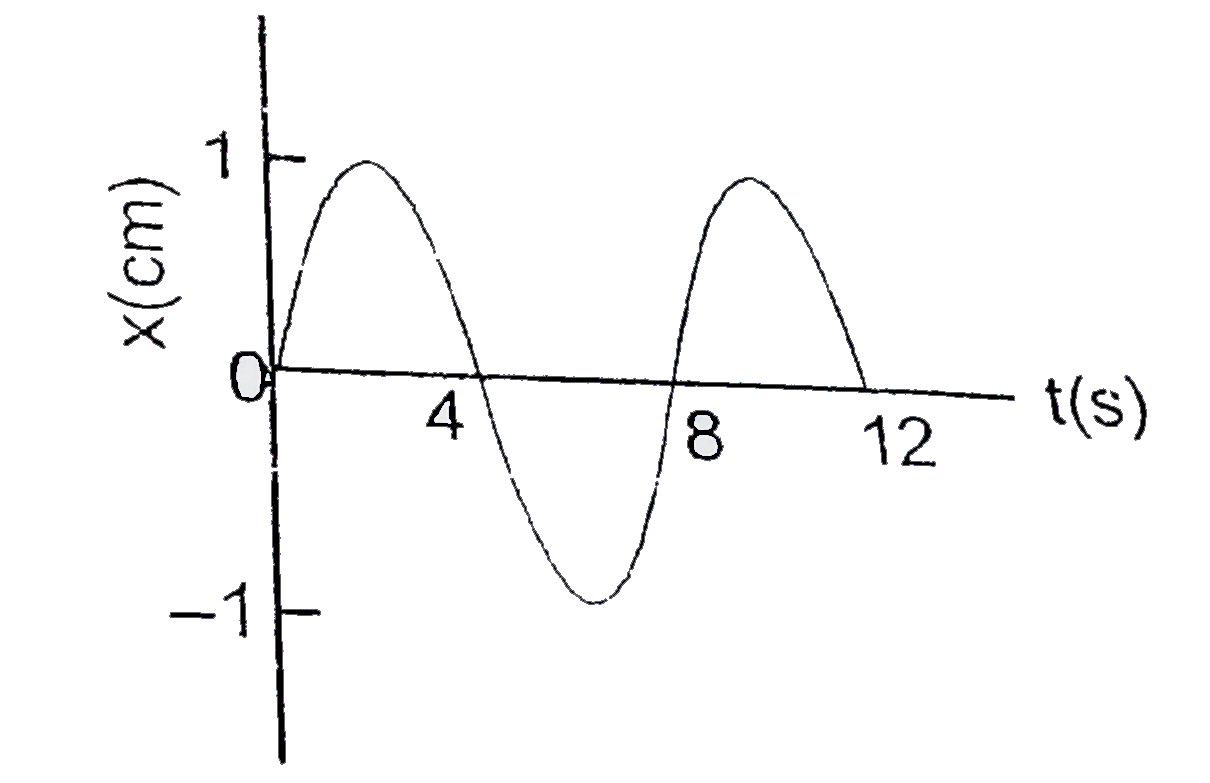
View Solution
