A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
To solve the problem of finding the amplitude of oscillations for a block of mass 'm' attached to a spring with force constant 'K', we can follow these steps:
1. Understanding the System:
- A block of mass 'm' is attached to a spring at its natural length. When the block is released, it will move downwards due to gravity and will start oscillating.
2. Identify Forces:
- The gravitational force acting on the block is Fg=mg.
- The spring force when the spring is stretched by a distance x is Fs=Kx.
3. Equilibrium Position:
- At the equilibrium position, the spring force equals the gravitational force:
Kx=mg
- From this, we can find the displacement x from the natural length to the equilibrium position:
x=mgK
4. Energy Conservation:
- When the block is released from the natural length, it will lose gravitational potential energy which will be converted into elastic potential energy in the spring.
- The change in gravitational potential energy when the block moves down by a distance x is:
ΔUg=mgx
- The elastic potential energy stored in the spring when it is stretched by the same distance x is:
Us=12Kx2
5. Setting Up the Energy Equation:
- At the maximum displacement (amplitude A), all the gravitational potential energy lost will equal the elastic potential energy stored in the spring:
mgA=12KA2
6. Solving for Amplitude:
- Rearranging the energy equation gives:
12KA2−mgA=0
- Factoring out A:
A(12KA−mg)=0
- This gives two solutions: A=0 (trivial solution) or:
12KA=mg⟹A=2mgK
7. Final Result:
- The amplitude of the subsequent oscillations is:
A=2mgK
- A block of mass 'm' is attached to a spring at its natural length. When the block is released, it will move downwards due to gravity and will start oscillating.
- The gravitational force acting on the block is Fg=mg.
- The spring force when the spring is stretched by a distance x is Fs=Kx.
- At the equilibrium position, the spring force equals the gravitational force:
Kx=mg
- From this, we can find the displacement x from the natural length to the equilibrium position:
x=mgK
- When the block is released from the natural length, it will lose gravitational potential energy which will be converted into elastic potential energy in the spring.
- The change in gravitational potential energy when the block moves down by a distance x is:
ΔUg=mgx
- The elastic potential energy stored in the spring when it is stretched by the same distance x is:
Us=12Kx2
- At the maximum displacement (amplitude A), all the gravitational potential energy lost will equal the elastic potential energy stored in the spring:
mgA=12KA2
- Rearranging the energy equation gives:
12KA2−mgA=0
- Factoring out A:
A(12KA−mg)=0
- This gives two solutions: A=0 (trivial solution) or:
12KA=mg⟹A=2mgK
- The amplitude of the subsequent oscillations is:
A=2mgK
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C.U.Q78videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -I (C.W)34videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
A block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
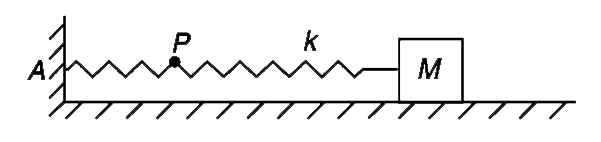 View Solution
View SolutionA block of mass 'm' is attached to a spring. Block is released from rest, when spring is in natural length. Block is along the pricipal axis of concave mirror and size of block is very small. When spring is in natural length then block is at a distance of 20 cm from the mirror, distance (in cm) in which the image formed by mirror oscillates is (mass of the block =5×10−2 kg, spring constant k=20 N//m)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 AmgπB2mgπC3mgπD4mgπ
AmgπB2mgπC3mgπD4mgπ - Question 2 - Select One
A block of mass m is attached to a spring of force constant k .Charges on the block is q. A horizontal electric field E is acting in the directions as shown.Block is released with the spring in unstretched position

block will execute SHM
(b) time period of osciallation is 2π√mk
(c) amplitude of oscillation is qEk
Block will oscillate but not simple harmonically
choose the correct answerAa and b are trueBd is trueCa,b,c are trueDa,b,c,d are true - Question 3 - Select One
Block A of mass m is placed on a plank B . A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initialy spring is in the natural length, and the system is at rest. Find the maximum compression in the spring, if the plank B is moved with a constant acceleration 'a' . (All the surface are smooth) :
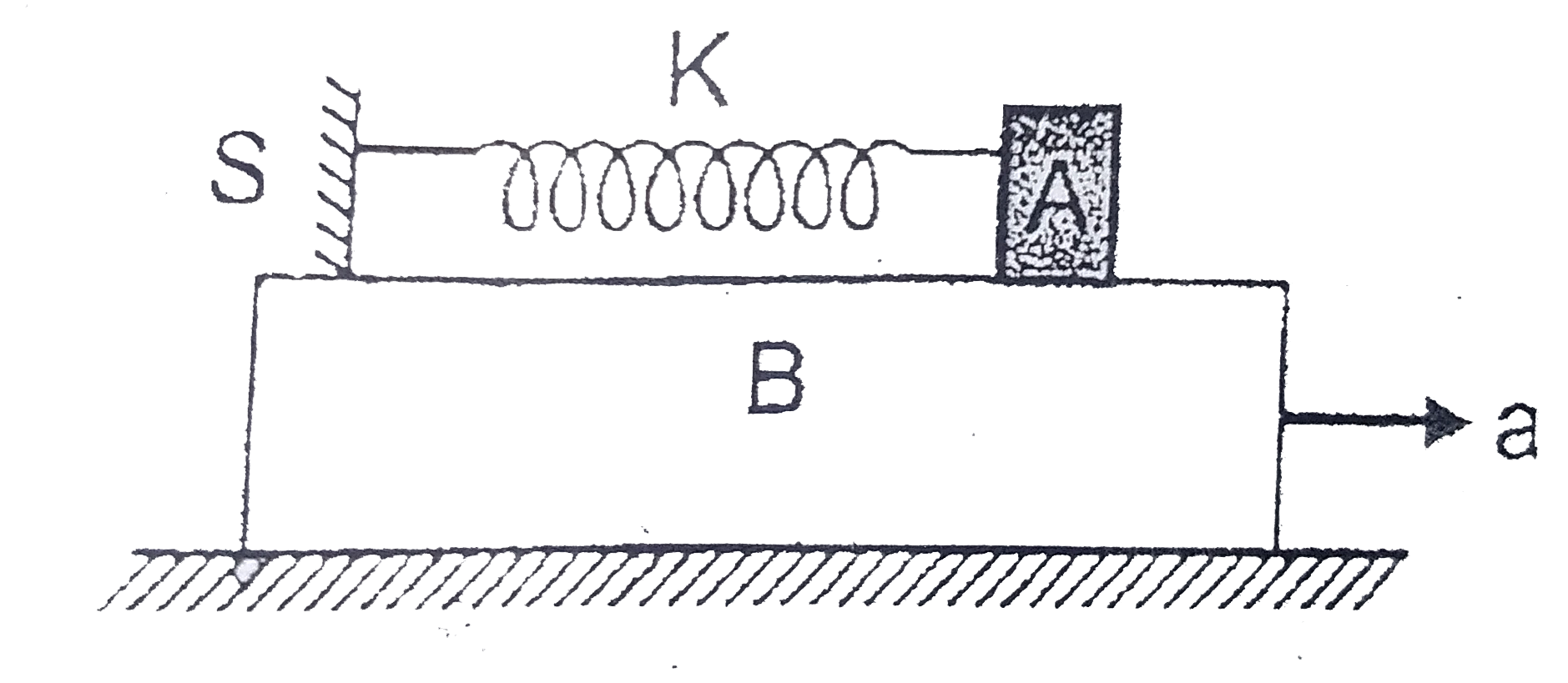 Ama2KB2maKCmaKD2maK
Ama2KB2maKCmaKD2maK
A block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
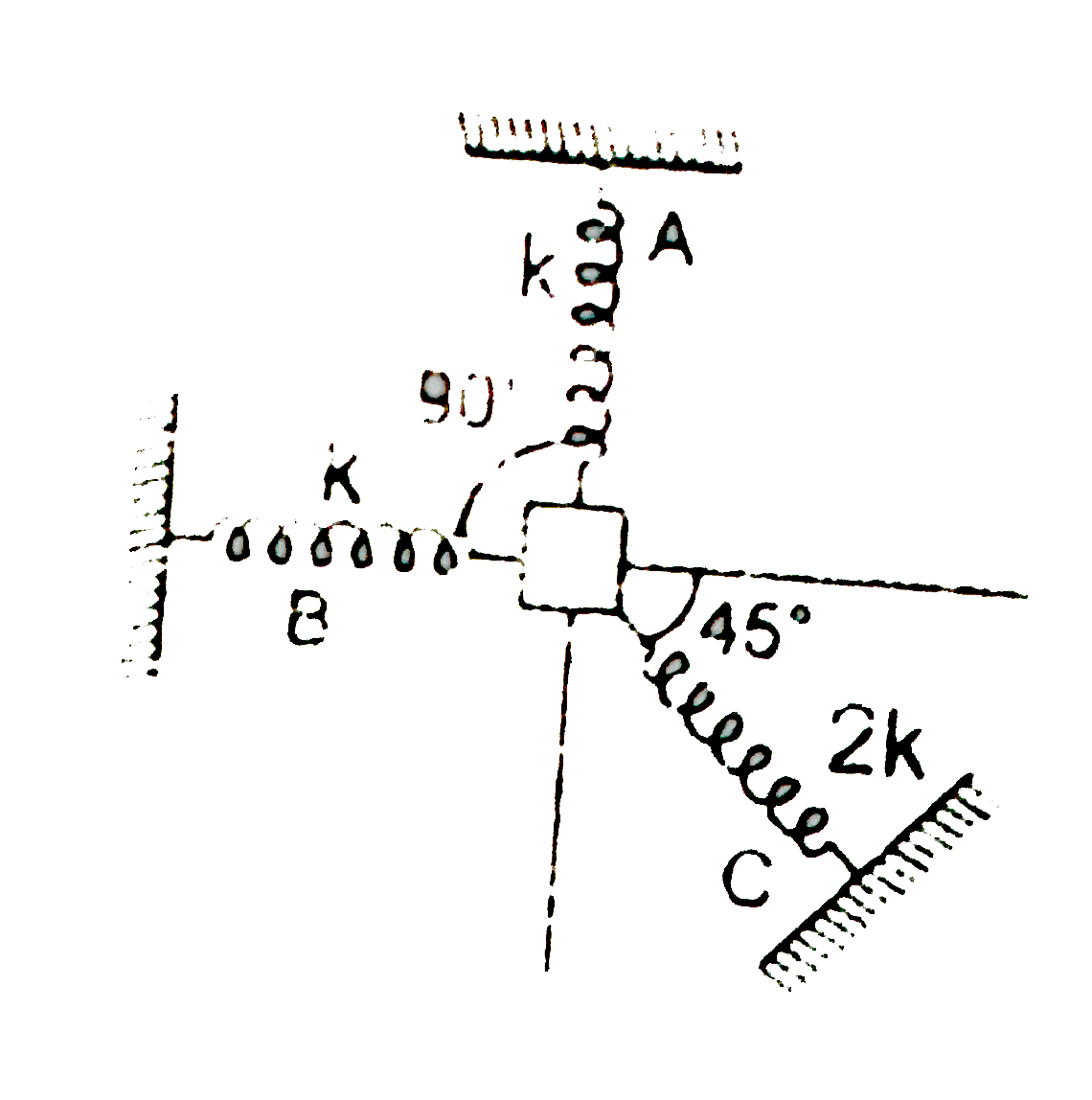 View Solution
View SolutionTwo blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
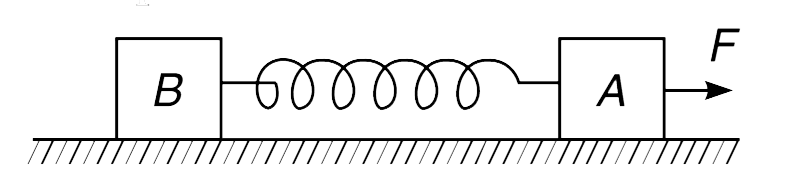 View Solution
View SolutionFigure-2.109 shows a block A on a smooth surface attached with a spring of force constant k to the ceiling. In this state spring is in its natural lengthl. The block A is connected with a massless and frictionless string to another identical mass B hanging over a light and smooth pulley. Find the distance moved by A before it leaves contact with the ground
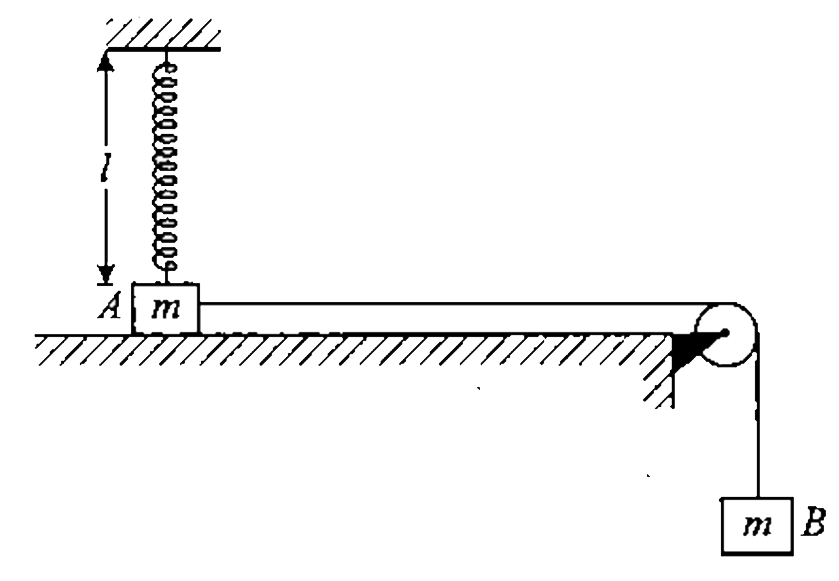 View Solution
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.
 View Solution
View SolutionBlock A of mass m is placed on a plank B. A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initially spring is in its natural length. If the plank B is given an acceleration a, then maximum compression in the spring is xmak. Find the value of x (All the surface are smooth)
 View Solution
View Solution

