In the diagram shown find the time period of pendulum for small oscillations
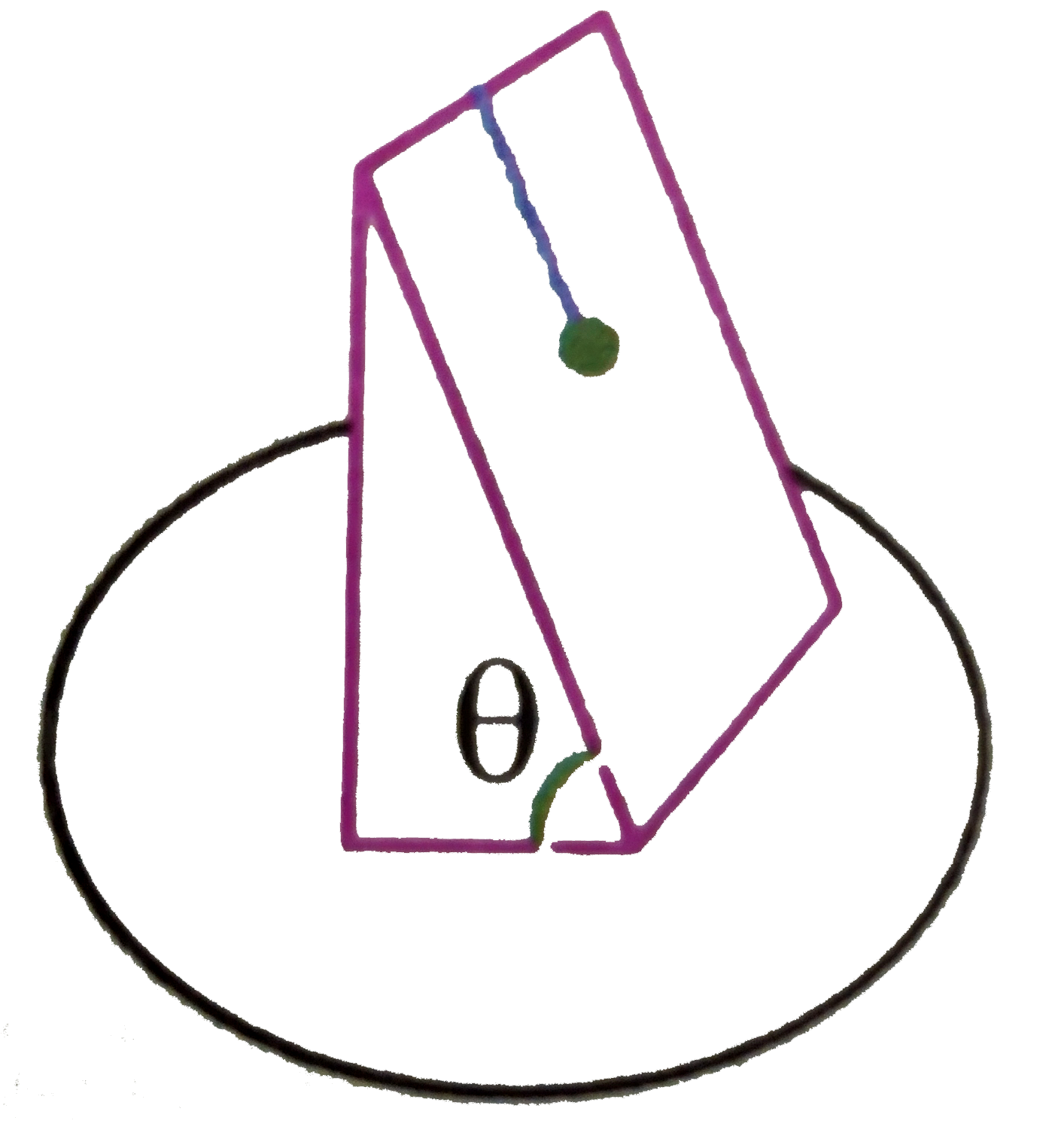
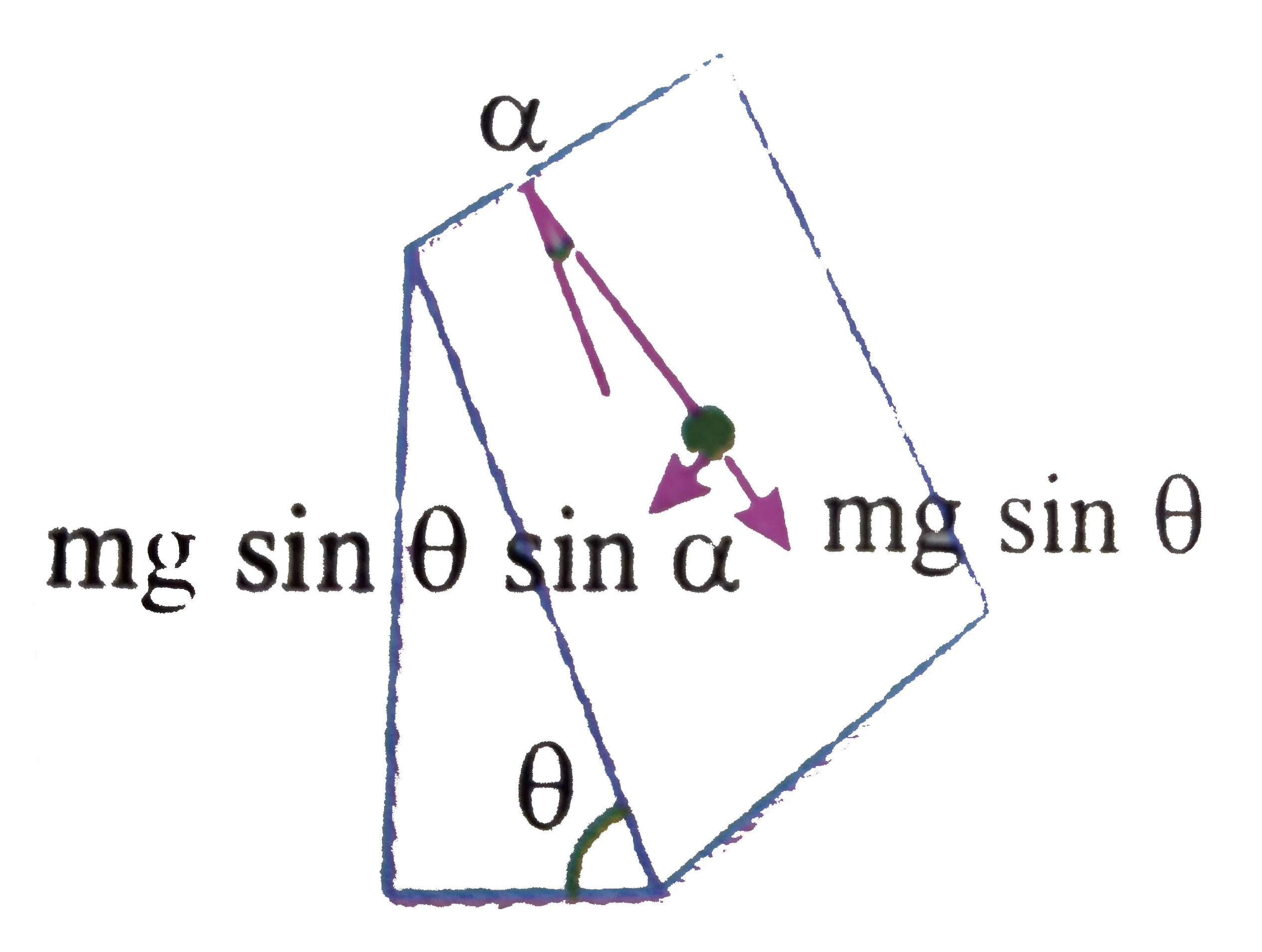
For smaller values of α,sinα≈α
F≈−(mgsinθ)α⇒ma=−(mgsinθ)yl
a=−(gsinθl)y=−ω2y
ω=√gsinθl⇒T=2π√lgsinθ
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C.U.Q
78 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -I (C.W)
34 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
A simple pendulum is suspnded from the ceilignof a car accelerating uniformly on a horizontal road.If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
View SolutionA uniform meter stickis suspended through a small pin hole at the 10 cm mark. Find the time period of small oscillation about the point of suspension.
View Solution
Knowledge Check
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
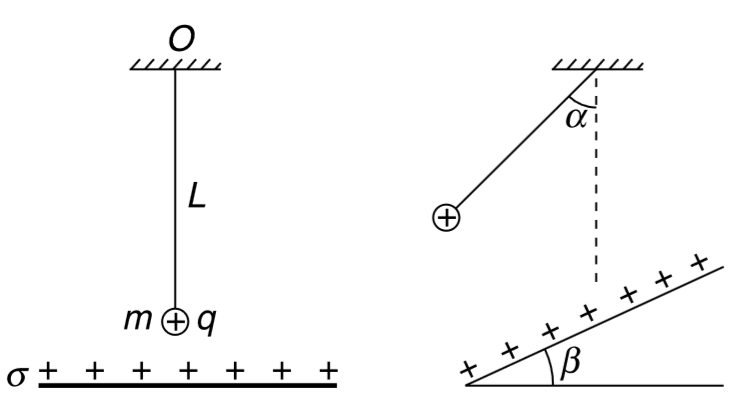
A2π√m6kB2π√11m6KC2π√6m11KD2π√mKThe bob of a pendulum of mass 'm' suspended by an inextensible string of length L as shown in the figure carries a small charge 'q' . An infinite horizontal plane conductor with uniform surface charge density sigma1 is placed below it . What will be the time period of the pendulum for small amplitude oscillations ?
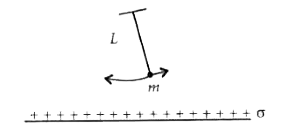 A2π ⎷L(g−mgε0σ)B ⎷L(g−mgε0)C12π ⎷L(g−qσε0m)D2π ⎷L(g−qσε0m)
A2π ⎷L(g−mgε0σ)B ⎷L(g−mgε0)C12π ⎷L(g−qσε0m)D2π ⎷L(g−qσε0m)In the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
 A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
A pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of σC/m2. [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle β with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
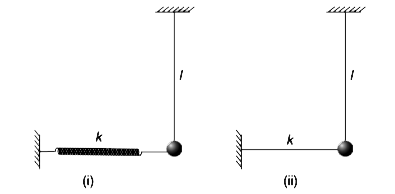
View SolutionA simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
View SolutionA uniform ring of radius 'R' is suspended from a horizontal nail 'A' as shown. Find time period of its small oscillations.

View SolutionA small block oscillates back and forth on as smooth concave surface of radius R figure. Find the time period of small oscillation.

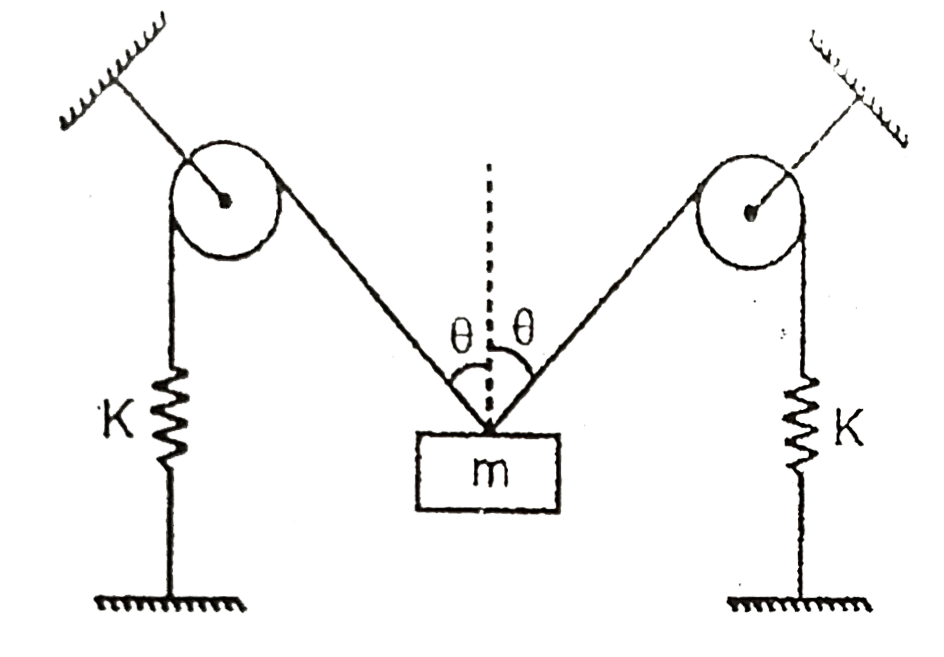
View SolutionA system is shown in the figure. The force The time period for small oscilations of the two blocks will be

View Solution
