A mass of 2kg oscillates on a spring with force constant 50N/m. By what factor does the frequency of oscillation decrease when a damping force with constant b=12 is introduced ?
Video Solution
Text Solution
ωo=√502=5Hz,ω=√ω2o−(b2m)2=√52−32=4Hz so 'ω' reduces by 1Hz or 20%
|
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:C.U.Q
Explore 78 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL -I (C.W)
Explore 34 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
Knowledge Check
Two spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
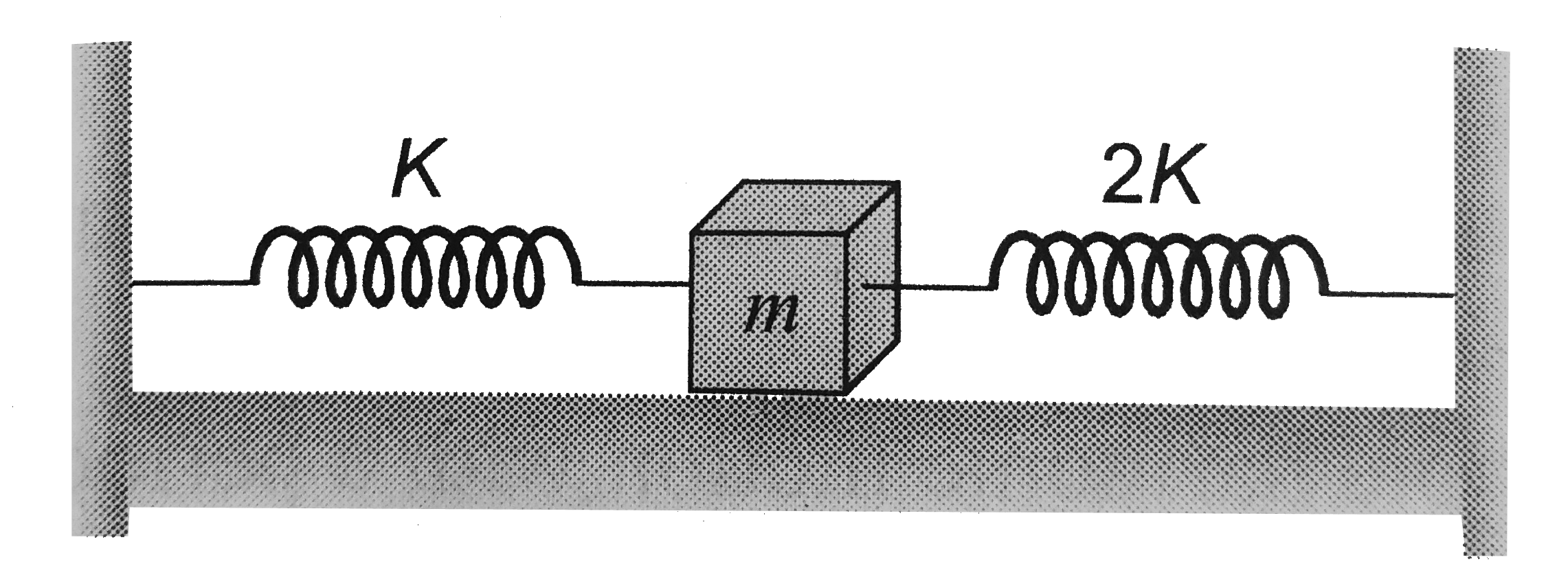 A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)If a body of mass 0.98 kg is made to oscillate on a spring of force constant 4.84 N/m the angular frequency of the body is
A1.22 rad/sB2.22 rad/sC3.22 rad/sD4.22 rad/sIf the mass of an osicllator is numerically equal to its force constant, then the frequency of oscillation will be
AπB2πC1/πD1/2π
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
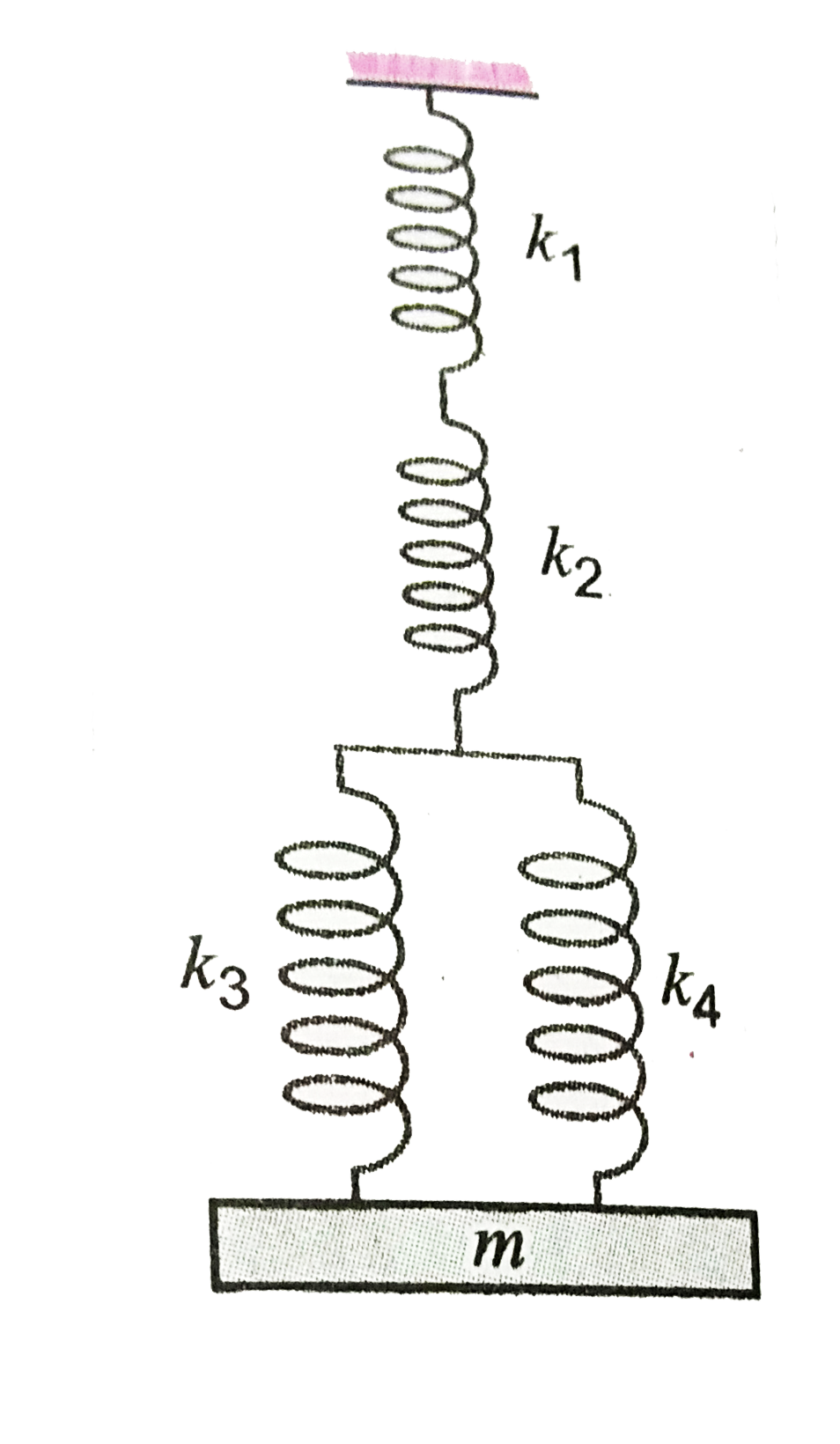
View SolutionA body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate (a) Angular frequncy , (b) Frequency of vibrations.
View SolutionA body of mass 2 kg is made to oscillate using a spring of force constant 8Nm−1 find (i) angular frequency (ii) frequency of vibration (iii) time period of vibration.
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View Solution