A particle starts SHM from mean position O executing SHM A and B are the two point at which its velocity is zero . It passes through a certain point P at time $t_{1} = 0.5 and t_{2} = 1.5 s$ with a speed of $3 m / s$ .

i. The maximum speed .......
ii. ratio $A P / P B$ .....

A

$\frac{\sqrt{2}}{\sqrt{2} + 1}$

B

$\frac{\sqrt{2} - 1}{\sqrt{2} + 1}$

C

$\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}}$

D

$\frac{\sqrt{2} + 1}{\sqrt{2} - 1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

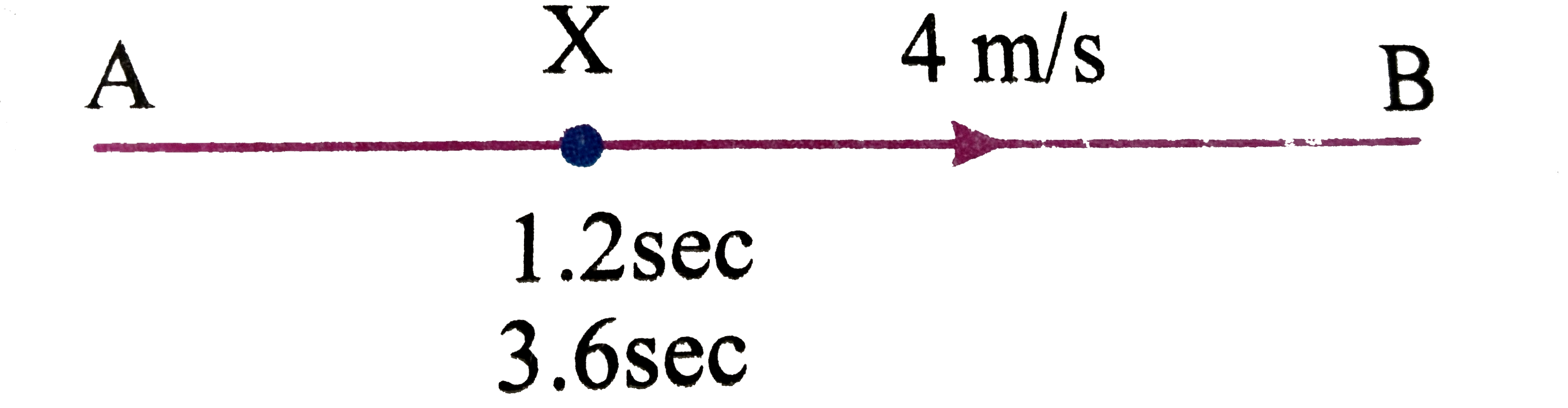
$T = 4.8 sec, t = \frac{1.2}{2} = 0.6 sec = \frac{T}{8}$
$x = - \frac{A}{\sqrt{2}}, \frac{A X}{X B} \Rightarrow \frac{A - | x |}{A + | x |}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A particle is executing SHM on a straight line. A and B are two points at which its velocity is zero. It passes through a certain point P(APltBP) at successive intervals of 0.5s and 1.5 s with a speed of 3m/s.
Athe maximum speed of particle is $3 \sqrt{2}$ m/s
Bthe maximum speed of particle is $\sqrt{2} \frac{m}{s}$ .
Cthe ratio (AP/BP) is $\frac{\sqrt{2} - 1}{\sqrt{2} + 1}$
Dthe ratio AP/BP is $\frac{1}{\sqrt{2}}$
Question 2 - Select One or More
A particle is executing SHM on a straight line. A and B are two points at which its velocity is zero. It passes through a certain point $P (A P < B P)$ at successive intervals of 0.5 sec and 1.5 sec with a speed of 3 m/s. Then
AThe maximum speed of particle is $3 \sqrt{2}$ m/s
Bthe maximum speed of particle is $\sqrt{2}$ m/s
Cthe ratio $\frac{A P}{B P} is \frac{s q r 2 - 1}{\sqrt{2} + 1}$
Dthe ratio $\frac{A P}{B P} is \frac{1}{\sqrt{2}}$
Question 3 - Select One
A particle starts its $S H M$ from mean position at $t = 0$ . If its time period is $T$ and amplitude $A$ then the distance travelled by the particle in the time from $t = 0 \to t = \frac{5 T}{A}$ is
A $A$
B $3 A$
C $4 A$
D $5 A$

NARAYNA-OSCILLATIONS-LEVEL -III

Home
Ask Doubt
Profile