A bob of mass M is hung using a string of length l. A mass m moving with a velocity u pierces thorugh the bob and emerges out with velocity u3 horizontally. The frequency of small oscillations of the bib, considering A as amplitude is,
12π√3μ2MA
12π√2m3MA
12π(2μ3MA)
12π(3μ2MA)
The correct Answer is:C
Using momentum conservation we get,
μ=Mv+m.u3∴V=23μM
K.E. at mean position of the bob
=12Mv2=12M49m2u2M2=2m2u29M
Comparing with K.E.=12Mω2A2 at mean position, We getω2=4m2u29M2A2 or ω=2μ3MA
=2πv⇒v=12(2μ3MA)
∴ Frequency (C ) is correct.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I2videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage33videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
A bullet of mass m strikes a pendulum bob of mass 2m with velocity u es shown in figure. If passes through and emerges but with a velocity u/2 from bob. The length of the pendulum bob is l=2m. If the minimum value of u for which the pendulum bob completes full circle is 10Xm/s, then find X.
(Take g=10m/s2)
 View Solution
View SolutionA pendulum of string length l = 2m and bob of mass M Is hit by a bullet with initial velocity u which completely penetrates through it and leaves the bob with velocity 3u4. If M100 is the mass of bullet, then the minimum initial velocity of bullet to make the bob to complete vertical circle is......m/s (g=10m/s2)
View Solution
Knowledge Check
- Question 1 - Select One
A bullet of mass m strikes a pendulum bob of mass M with velocity u. It passes through and emerges out with a velocity u/2 from bob. The length of the pendulum is l. What should be the minimum value of u if the pendulum bob will swing through a complete circle?
A2Mm×√5glBM2m√5glC2Mm×1√5glDM2m×1√5gl - Question 2 - Select One
A ball of mass '2m' moving with velocity uˆi collides with another ball of mass 'm' moving with velocity −2uˆi. After the collision, mass 2m moves with velocity u2(ˆi−ˆj). Then the change in kinetic energy of the system ( both balls ) is
AzeroB32mu2C32mu2(1−12√2)D32mu2(1+12√2) - Question 3 - Select One or More

A simple pendulum consists of a bob of mass m and a light string of length l as shown in the fig. another identical ball moving with the small velocity v0 collides with the pendulum's bob and sticks to it. For this new pendulum of mass 2 m, mark out the correct statements (s).ATime period of the pendulum is 2π√lg.BThe equation of motion for this pendulum is θ=v02√glsin[√glt]CThe equation of motion for this pendulum is θ=v02√glcos[√glt].DTime period of the pendulum is 2π√2lg.
A bob of mass m is suspended by a light inextensible string of length l from a fixed point such that it is free to rotate in a vertical plane. The bob is given' a speed of √4gl horizontally. The, height of the bob from the lower most point where the string just becomes slacked is nl3. Find n.
View SolutionA smooth hollow U shaped tube of mass 2m is lying at rest on a smooth horizontal table. Two small balls of mass m, moving with velocity u enter the tube simultaneously in symmetrical fashion. Assume all collisions to be elastic. Find the final velocity of the balls and the tube.
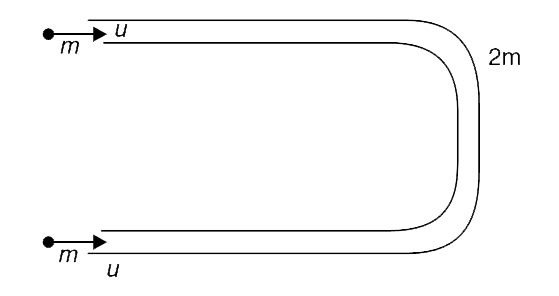 View Solution
View SolutionA bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
View SolutionA bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The horizontal coordinate of the intital position of the bob w.r.t. the point of firing of the bullet is nView SolutionA body of mass m moving with velocity uˆi collides elastically with a body at rest of mass 3m and then the final velocity of body mass m is v ˆj. Find the relation between v and u
View Solution

