A thin uniform rod of length L=100cm is to be pivoted about some point passing through the rod is allowed to swing as a physical pendulum. For this situation mark the correct statement (s) [take g=10m/s2]
If the rod is pioted at 29cm (approximately) away form centre of rod then it will perform SHM with least time period
If the rod is pivoted at 15cm (approximately) away form centre of rod then it will performs SHM with least time period.
The least time period (approximately) with which rod can oscillate is 1.5s
There are two possible loaction of pivot about which rod can perform SHM with leats time period.
The correct Answer is:A, C, D
T=2π√Imgd
where I is momet of inertia of road about P.

i.e. I=mL212+md2
For minimum time period dTdd=0
d=l√12=29cm
Value of minimum time T=1.5sec
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - ASSERTION & REASON QUESTIONS13videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - NCERT BASED QUESTIONS1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
A uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View SolutionA thin uniform rod of lenth 120cm is made to oscillate about an axis passing through it end. Find the period and other points about which it has the same time period (g=9.8ms−2).
View Solution
Knowledge Check
- Question 1 - Select One
The radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
AL2√3BL212CL√3DL√2 - Question 2 - Select One
The radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
AL√12BL2√12CL√3DL√2 - Question 3 - Select One
A thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
A2π√lgB2π√2l3gC2π√3l2gD2π√l3g
A rod of length l and mass m is capable of rotating freely about an axis passing through a hole at the end. The period of oscillation of this physical pendulum is
View SolutionA uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
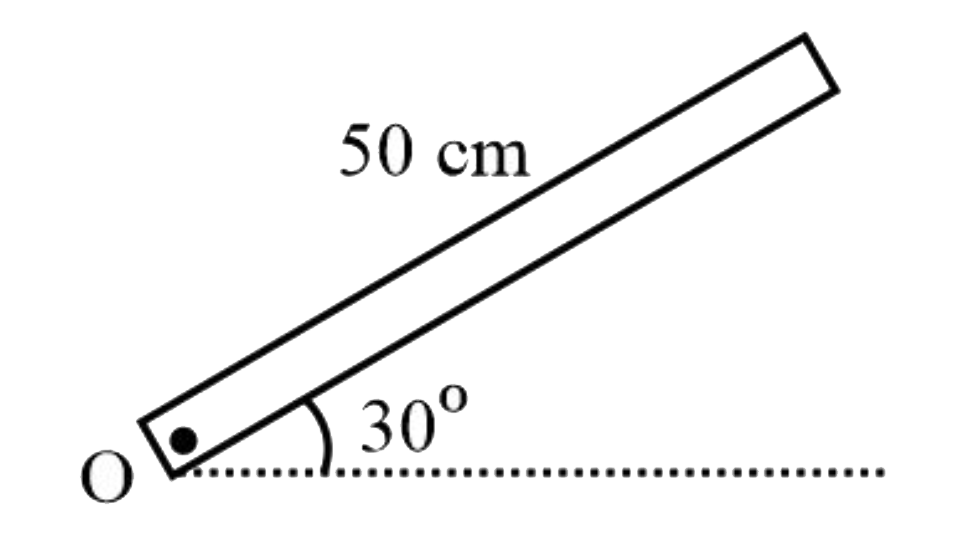 View Solution
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is
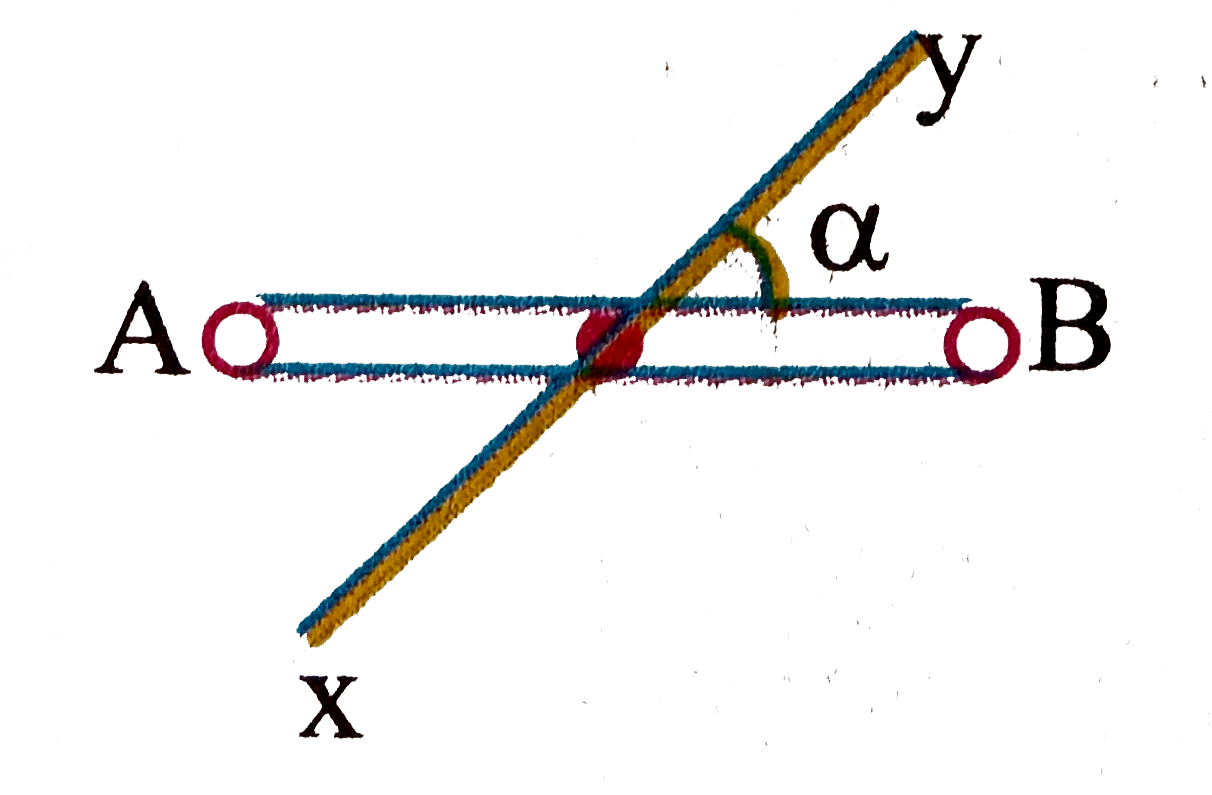 View Solution
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its cenre of mass rises to a maximum height of :
View Solution

