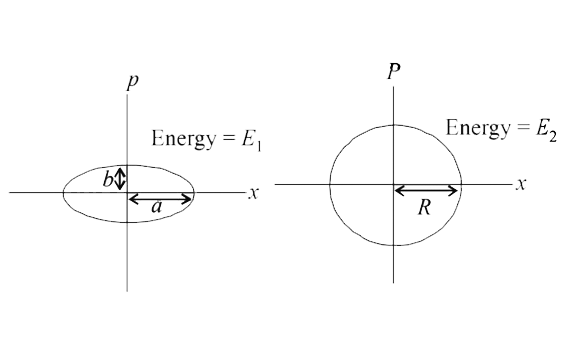
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies (omega_1) and (omega_2) and have total energies (E_1 and E_2), respectively. The variations of their momenta (p) with positions (x) are shown (s) is (are).

A

$E_{1} ω_{1} = E_{2} ω_{2}$

B

$\frac{ω_{2}}{ω_{1}} - n^{2}$

C

$ω_{1} ω_{2} = n^{2}$

D

$\frac{E_{1}}{ω_{1}} = \frac{E_{2}}{ω_{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, D

For forst oscillator $E_{1} = \frac{1}{2} m ω_{1}^{2} a^{2}$ , and $p = m v = m ω_{1} a = b \Rightarrow \frac{a}{b} = \frac{1}{m ω_{1}} \dots \dots . (i)$
for second oscillator
$E_{2} = \frac{1}{2} m ω_{2}^{2} R^{2}$ , and $m ω_{2} = 1 \dots \dots \dots \dots . (i i)$
$(\frac{a}{b}) = \frac{ω_{2}}{ω_{1} = n^{2}}$
$\frac{E_{1}}{ω_{1}^{2} a^{2}} = \frac{E_{2}}{ω_{2}^{2} R^{2}} \Rightarrow \frac{E_{1}}{ω_{1}} = \frac{E_{2}}{ω_{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies $ω_{1}$ and $ω_{2}$ and have total energies $E_{1}$ and $E_{2}$ repsectively. The variations of their momenta $p$ with positions $x$ are shown in figures. If $\frac{a}{b} = n^{2}$ and $\frac{a}{R} = n$ , then the correc t equation(s) is (are) :

A $E_{1} ω_{1} = E_{2} ω_{2}$
B $\frac{ω_{2}}{ω_{1}} = n^{2}$
C $ω_{1} ω_{2} = n^{2}$
D $\frac{E_{1}}{ω_{1}} = \frac{E_{2}}{ω_{2}}$
Question 2 - Select One
Two bodies of different masses $m_{1}$ and $m_{2}$ have equal momenta. Their kinetic energies $E_{1}$ and $E_{2}$ are in the ratio
A $\sqrt{m_{1}} : \sqrt{m_{2}}$
B $m_{1} : m_{2}$
C $m_{2} : m_{1}$
D $m_{1}^{2} : m_{2}^{2}$
Question 3 - Select One
For a linear harmonic oscillator, its potential energy, kinetic energy and total energy given by $E_{P}, K_{K} and E_{T}$ respectively. Its maximum acceleration is given by
A $\sqrt{\frac{2 E_{P}}{m}}$
B $\sqrt{\frac{2 E_{K}}{m}}$
C $\sqrt{\frac{2 E_{T}}{m A}}$
D $\frac{2 E_{T}}{m A}$

NARAYNA-OSCILLATIONS-MULTIPLE ANSWER QUESTIONS

Home
Ask Doubt
Profile