A man of 50kg is standing at one end on a boat of length 25m and mass 200kg.If he starts running and when he reaches the other end, has a velocity 2ms−1 with respect to the boat.The final velocity of the boat is
23ms−1
25ms−1
85ms−1
83ms−1
The correct Answer is:B
To solve the problem, we can use the principle of conservation of momentum. Let's break down the steps:
Step 1: Understand the system
We have a man with a mass of m1=50kg and a boat with a mass of m2=200kg. The length of the boat is 25m. The man runs from one end of the boat to the other and reaches a velocity of vm,boat=2m/s with respect to the boat.
Step 2: Define the velocities
Let:
- vb = final velocity of the boat with respect to the ground.
- vm = final velocity of the man with respect to the ground.
The velocity of the man with respect to the ground can be expressed as:
vm=vm,boat+vb
Substituting the known value:
vm=2m/s+vb
Step 3: Apply conservation of momentum
Initially, both the man and the boat are at rest, so the total initial momentum is zero:
Initial momentum=0
When the man runs, the total momentum must still equal zero:
m1vm+m2vb=0
Substituting m1 and m2:
50kg⋅(2m/s+vb)+200kg⋅vb=0
Step 4: Solve for vb
Expanding the equation:
100kg m/s+50kg⋅vb+200kg⋅vb=0
Combining the terms:
100+250vb=0
Solving for vb:
250vb=−100
vb=−100250=−0.4m/s
Step 5: Conclusion
The final velocity of the boat is −0.4m/s. The negative sign indicates that the boat moves in the opposite direction to the man's movement.
We have a man with a mass of m1=50kg and a boat with a mass of m2=200kg. The length of the boat is 25m. The man runs from one end of the boat to the other and reaches a velocity of vm,boat=2m/s with respect to the boat.
Let:
- vb = final velocity of the boat with respect to the ground.
- vm = final velocity of the man with respect to the ground.
vm=vm,boat+vb
Substituting the known value:
vm=2m/s+vb
Initially, both the man and the boat are at rest, so the total initial momentum is zero:
Initial momentum=0
m1vm+m2vb=0
Substituting m1 and m2:
50kg⋅(2m/s+vb)+200kg⋅vb=0
Expanding the equation:
100kg m/s+50kg⋅vb+200kg⋅vb=0
Combining the terms:
100+250vb=0
Solving for vb:
250vb=−100
vb=−100250=−0.4m/s
The final velocity of the boat is −0.4m/s. The negative sign indicates that the boat moves in the opposite direction to the man's movement.
Topper's Solved these Questions
Similar Questions
The figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.

When the man reaches the end B, the distance moves . by the trolley with respect to ground is:View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
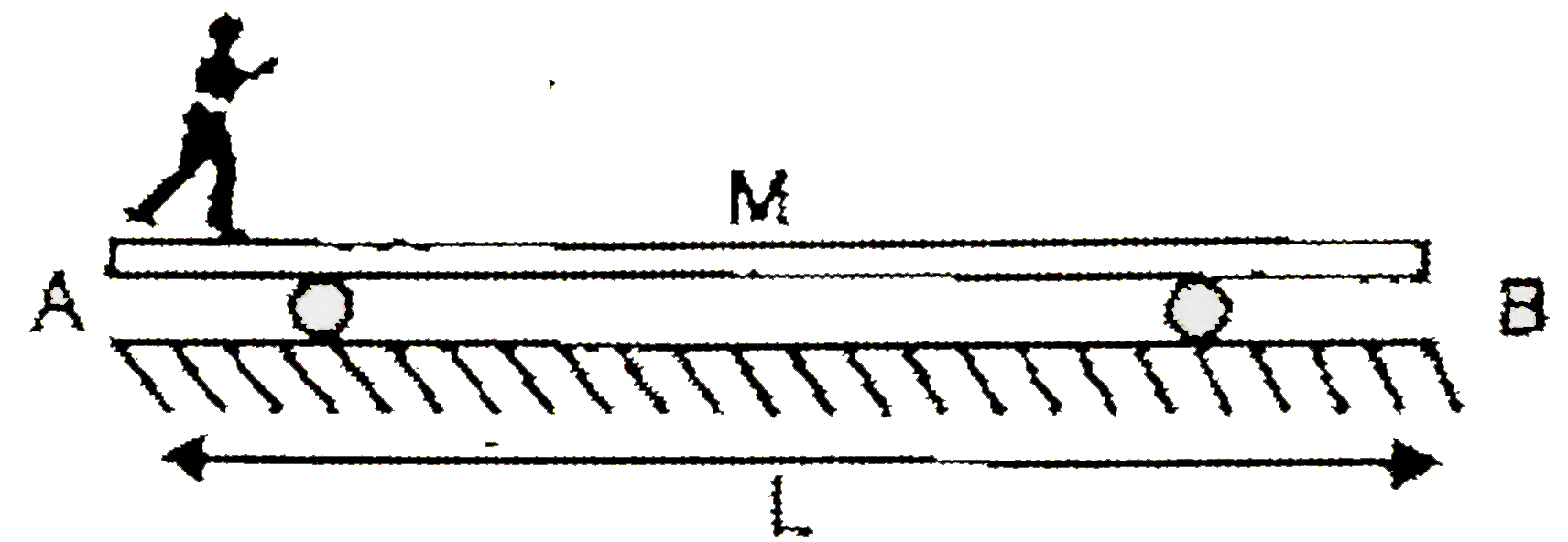
When the man starts moving, then the velocity of the trolley v2 with respect to ground will be:View Solution
Knowledge Check
- Question 1 - Select One
A boy of mass 50kg is standing at one end of a boat of length 9m and mass 400kg. He runs to the other end. The distance through which the centre of mass of the boat boy system moves is
A0B1mC2mD3m - Question 2 - Select One
A boy of mass m is standing at one end of a boat of mass M and length l. The boy walks to the other end, the displacement of the
ACM is zeroBboat is mlM+mCboy is mlM+mDboat is mMl - Question 3 - Select One
A boy (massof40kg) is standing at one end of a boat (mass of 60 kg) in still water. The length of the boat is 10m and the boy takes 2s to reach at other end of boat moving with constant speed. Assuming no friction between the boat and the water.
(i) The distance covered by the boat is 4m
(ii) The distance covered by the boy with respect to the ground is 6m.
(iii) The velocity of the boy with respect to the ground is <5m/s
(iv) The velocity of the boy is 3m/sA(i),(ii)B(ii),(iii)C(i),(ii),(iii)Dall options are correct
The figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
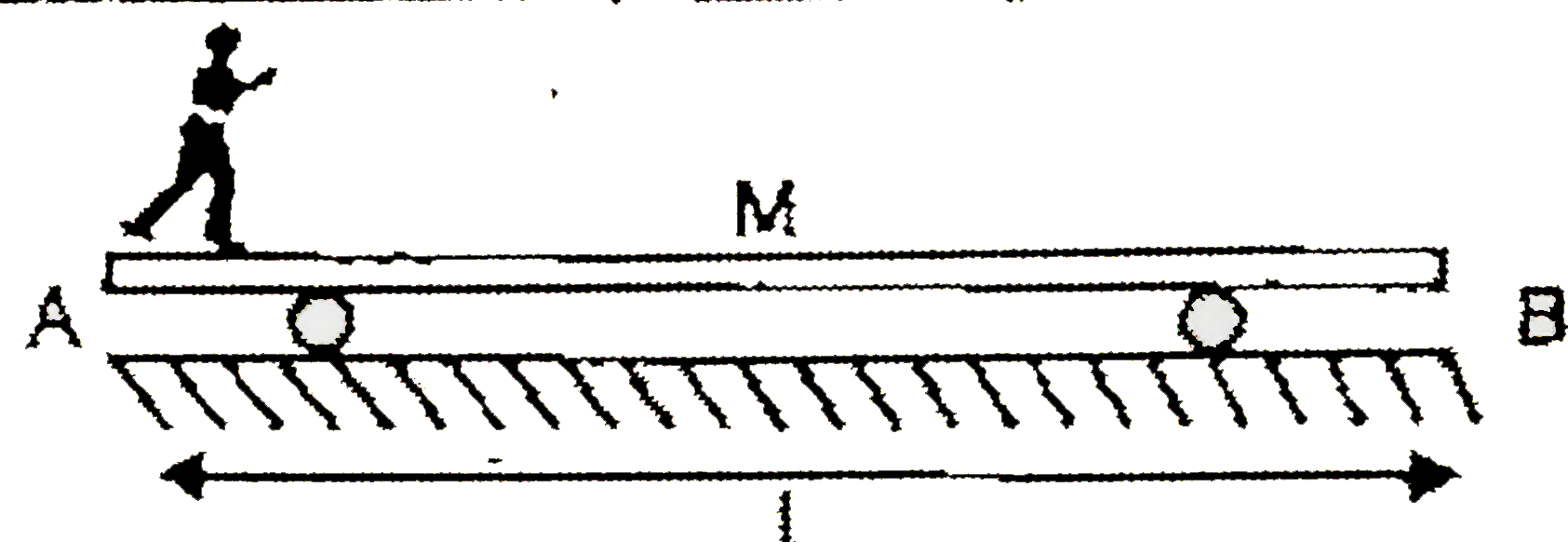
The time taken by the man to reach the other end is:View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
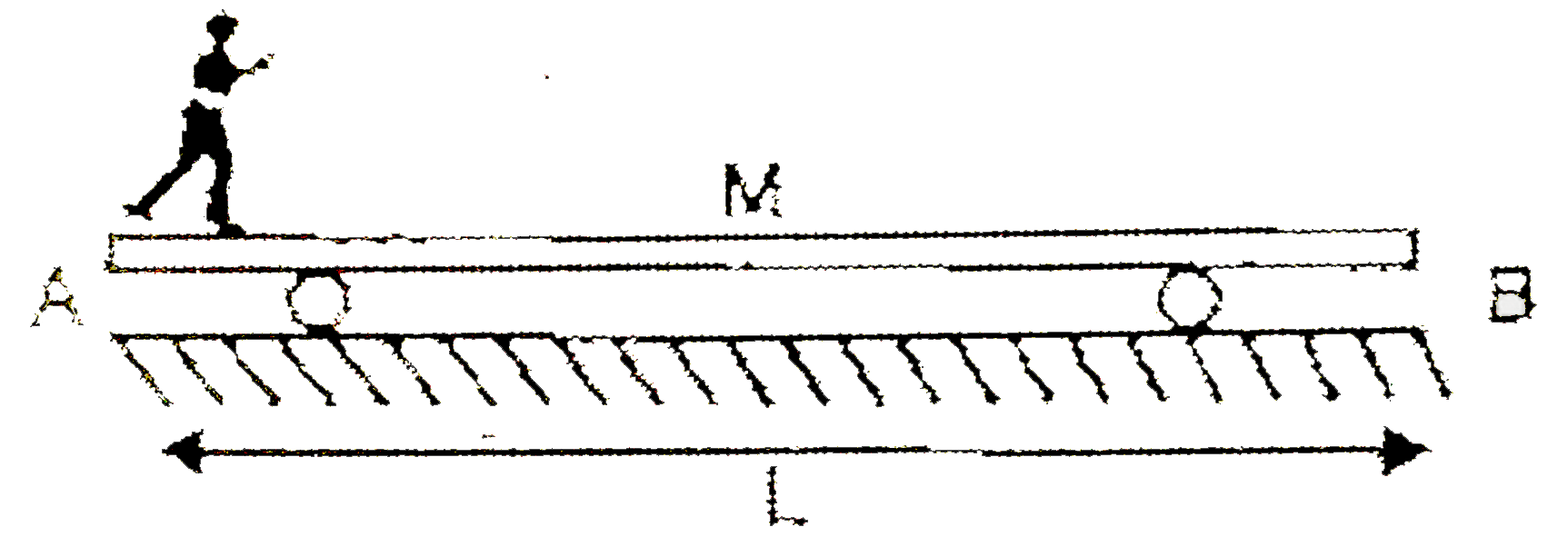
The velocity of the man with respect to ground v1 will be:View SolutionA boy of mass 30 kg is standing at one end on a stationary boat over a lake. The boat has a mass 70 kg and length 10 m. Now the boy walked to the other end of the boat. Relative to the ground
View SolutionA boy of mass 40kg is standing at one ned of the boat (mass : 80 kg) of length 6m in a river. Now the boy reaches to other end of the boat. Find the distance moved by the boat and the distance travelled by boy as seen from the bank of river.Assume that the system is at rest and no friction between the boat and the water.
View SolutionA boy having a mass of 40kg stands at one end A of a boat of length 2m at rest. The boy walks to the other end B of the boat and stops. What is the distance moved by the boat? Friciton exists between the feet of the boy and the surface of the boat. But the friction between the boat and the water surface may be neglected. Mass of the boat is 15kg.
 View Solution
View Solution

