Two equal spheres of mass m are in contact on a smooth horizontal table. A third identical sphere impinges symmetrically on them and reduces to rest. Then:

Coefficient of restitution is e=23
Loss of kinetic energy 16mu2 where u is velocity before impact
After the collision, velocity of equal mass sphere is u√3
Loss of kinetic energy 13mu2
The correct Answer is:A, B, C
From momentum conservation
mu=mvcos30+mvcos30,v=u√3
So, choice (c ) is correct.
For an oblique collision, we have to take components along normal i.e., along AB for sphere A and B.
vB=vA=e(uA−uB) , v−0=e[ucos30−0]
v=eu×√32 , v=e.v√3.√32, e=23
So, choice (a) is correct. Also, loss of kinetic energy
ΔK=12mu2−2(12mv2)
=12mu2−212m⎡⎣(u√3)2⎤⎦=16mu2
Topper's Solved these Questions
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Comprehension type
35 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Subjective type Questions
9 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - INTEGER TYPE QUESTIONS
8 Videos
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)
51 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
Similar Questions
Two equal sphere of mass m are in contact o a smooth horizontal table. A third identical sphere impinges symmetrically on them and is reduced to rest. Find e and the loss KE.

View SolutionTwo equal spheres of mass m are in contact on a smooth horizontal table. A third identical sphere impinges symmetrically on the and is reduced to rest. Prove that e=23 and find the loss in KE.
View Solution
Knowledge Check
Two equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
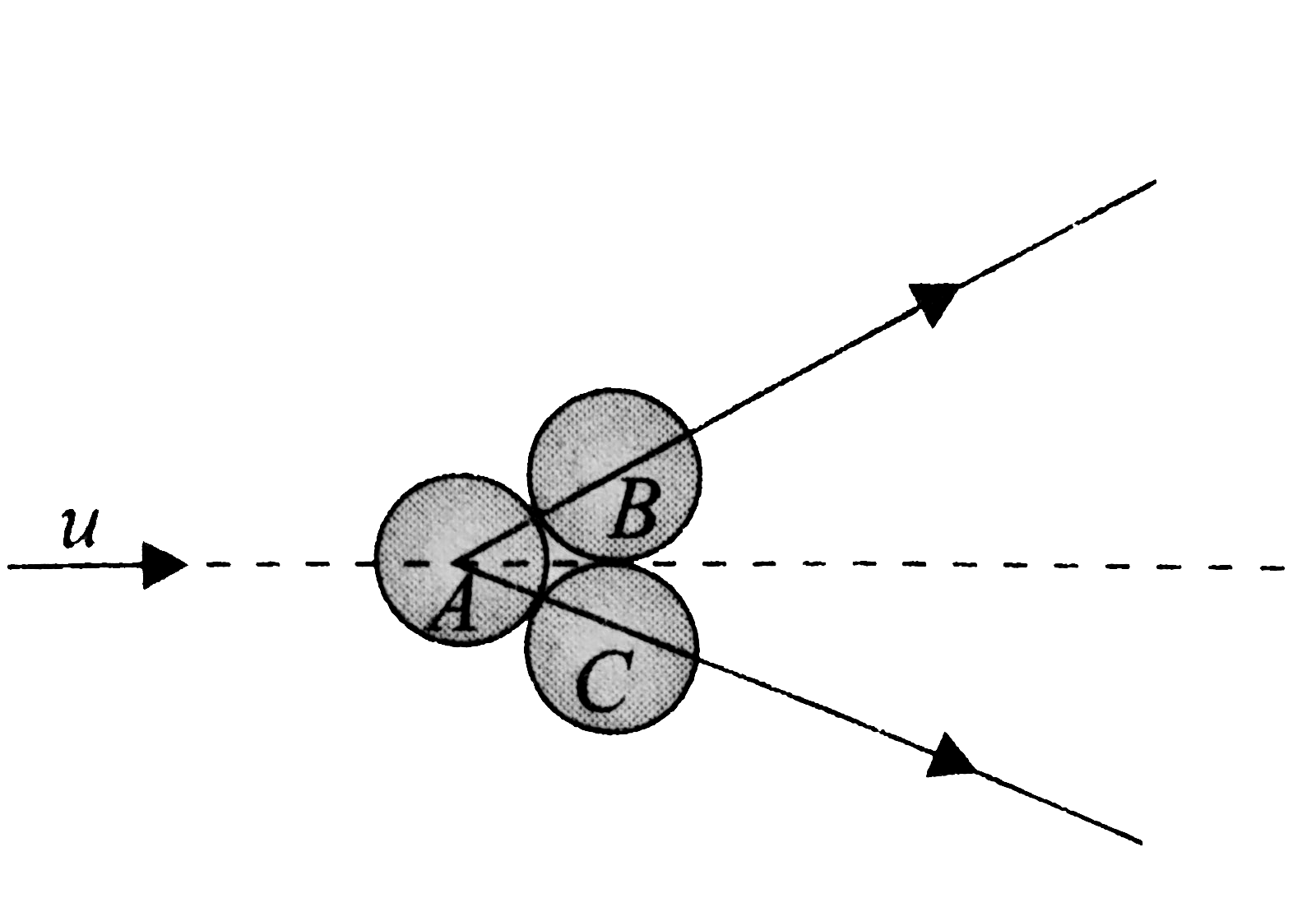
The coefficient of restitution between the two spheres A and B (or between A and C) isA1/3B1/4C2/3D3/4Two equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
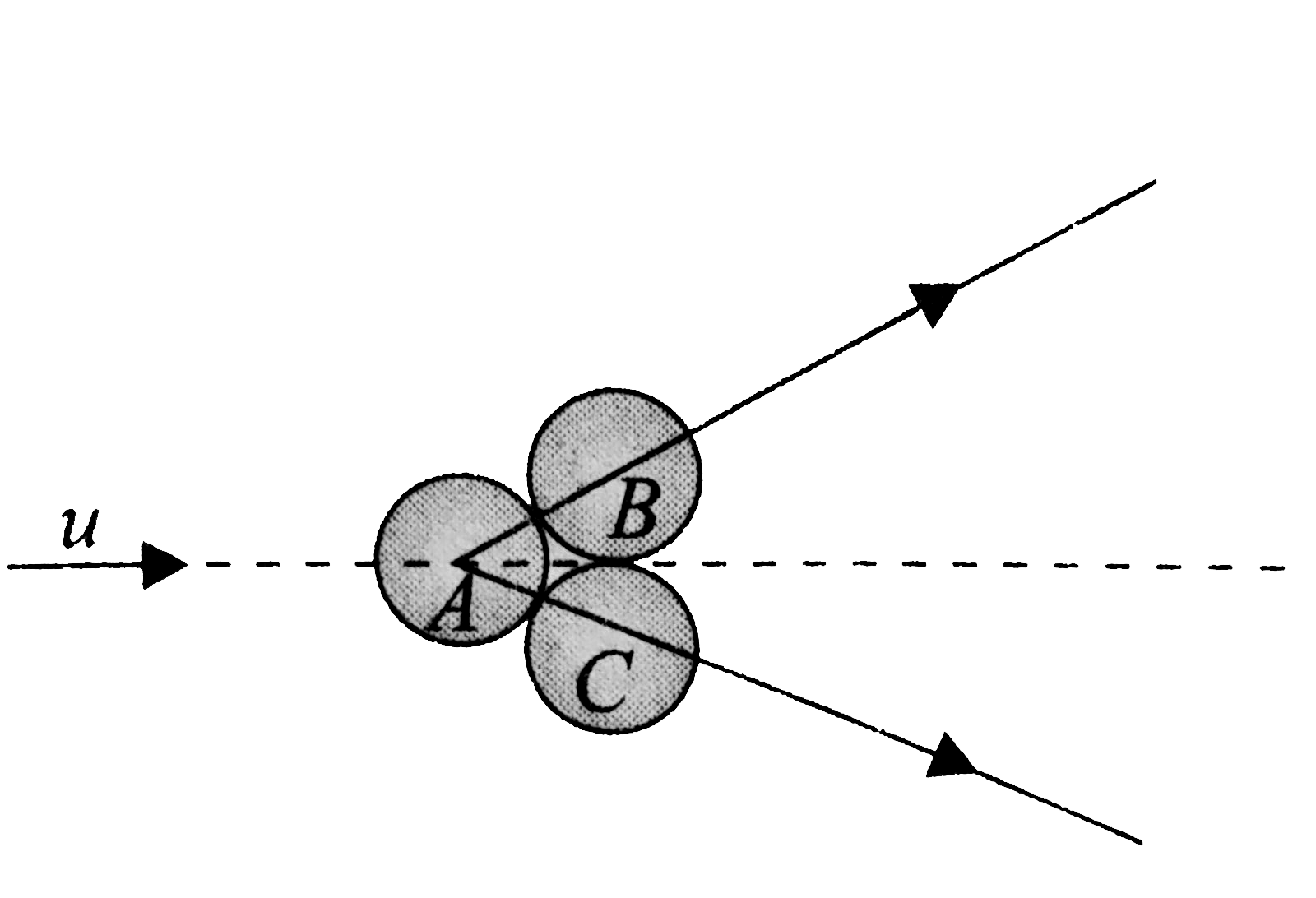
Find the velocity acquired by each of the spheres B and C after collision.Au√3B2u√3Cu2√3Du2Two equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
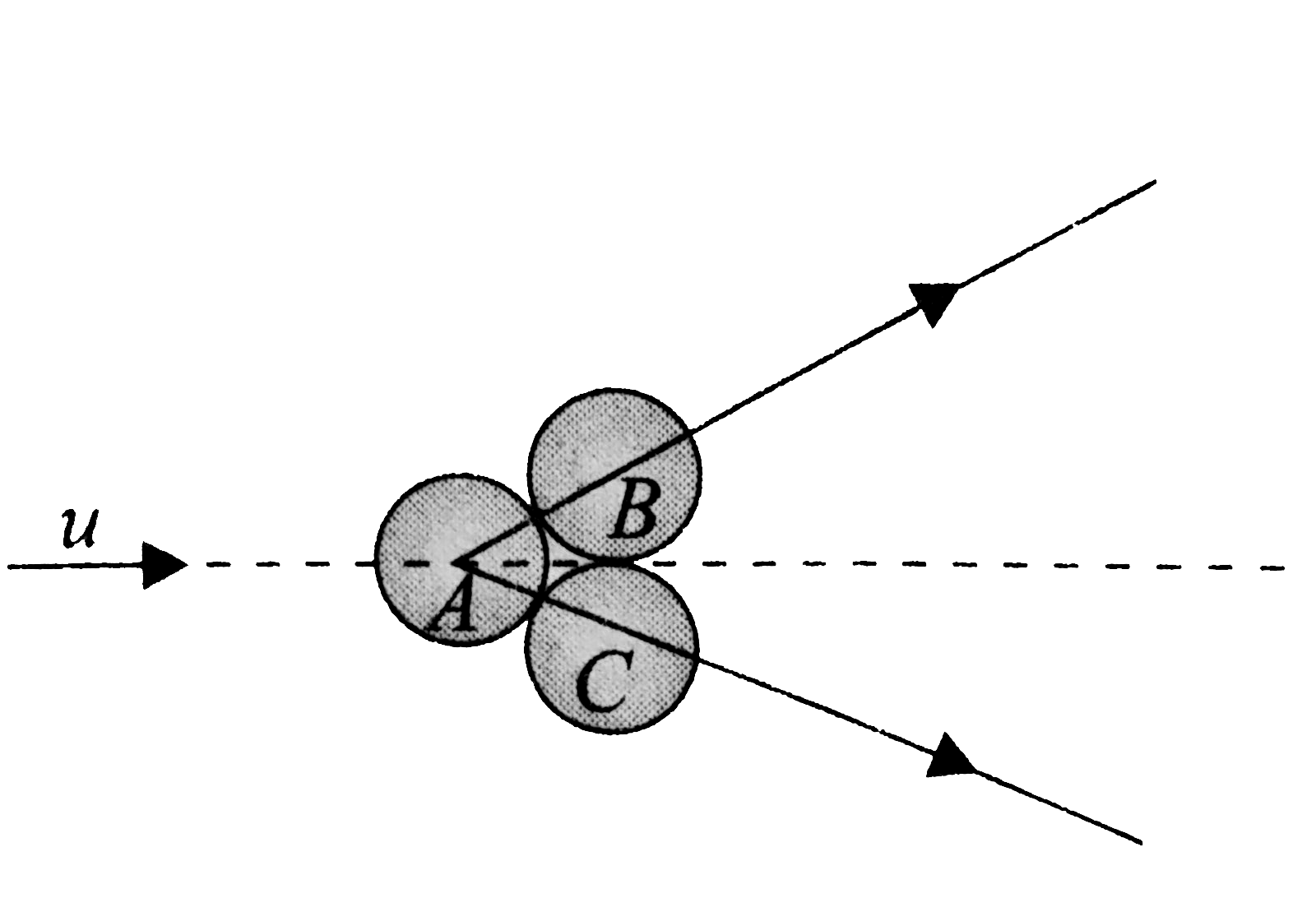
The loss of KE during collision isAmu28Bmu26Cmu23Dmu22
Two billiard balls of same size and mass are in contact on a billiard table. A third ball of same mass and size strikes them symmetrically and remains at rest after the impact. Find the coefficient of restitution between the balls?
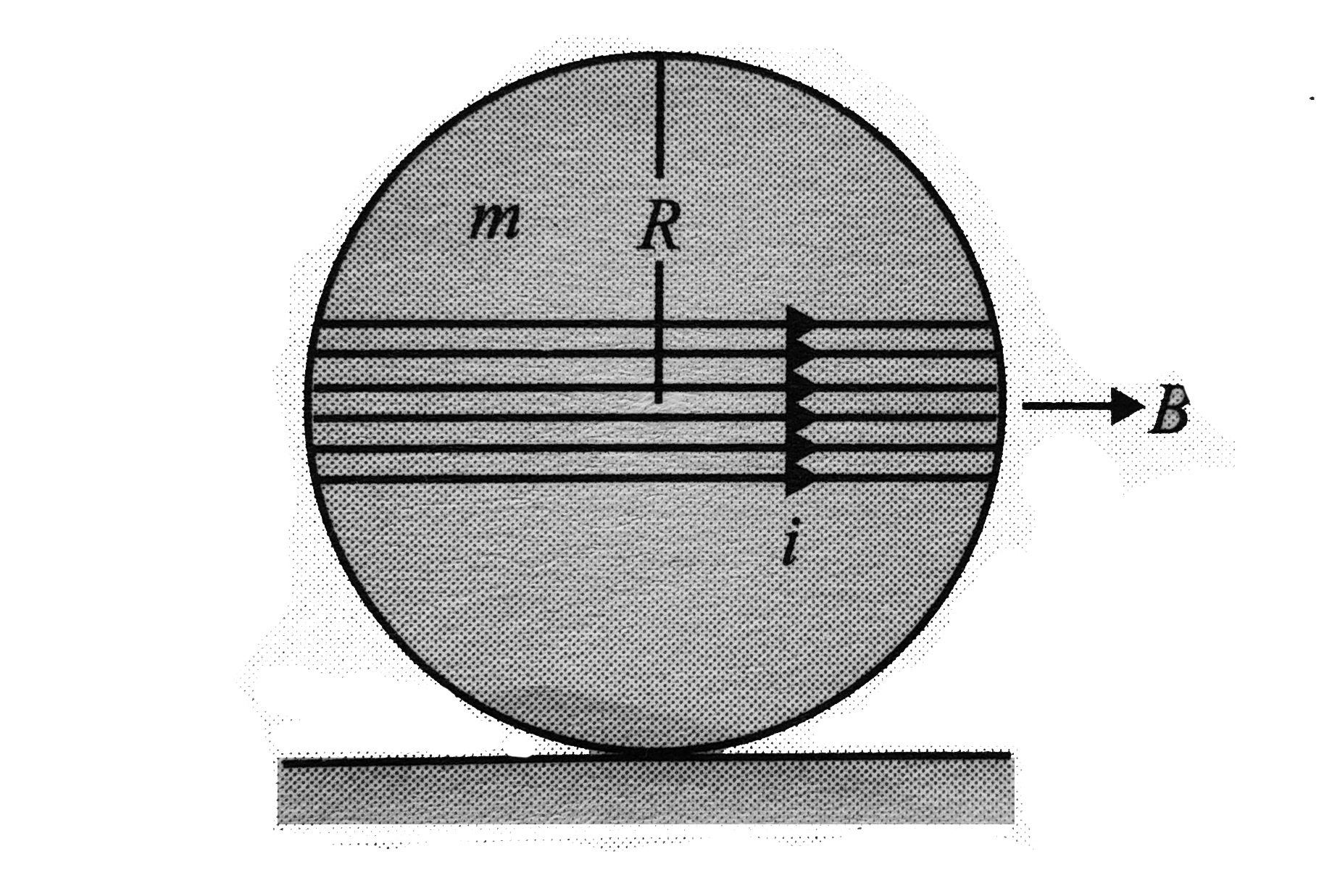
View SolutionA wire is wrapped N times over a solid sphere of mass m which is place on a smooth horizontal surface. A horizontal magnetic field of induction →B is present. Find the (a) torque (b) angular acceleration experienced by the sphere. Assume that the mass of the wire is negligible compared to the mass of the sphere.
View SolutionTwo identical billiard balls are in contact on a table. A third identical ball strikes them symmetrically and comes to rest after impact. The coefficient of restitution is :
View SolutionTwo small sphere each of mass m connected by a string of length 2l are kept on a smooth horizontal surface. A vertical force F is applied at the middle of the string. What is maximum value of F for which the sphere do not lose contact with the surface?

View SolutionA bullet of mass m is fired horizontally into a large sphere of mass M and radius R resting on a smooth horizontal table.

The bullet hits the sphere at a height h from the table and sticks to its surface. If the sphere starts rolling without slippng immediately on impact, then
View Solution
