A particle $(A)$ of mass $m_{1}$ elastically collides with another stationary particle $(B)$ of mass $m_{2}$ . Then :

A

$\frac{m_{1}}{m_{2}} = \frac{1}{2}$ and the particles fly a part in the opposite direction with equal velocities.

B

$\frac{m_{1}}{m_{2}} = \frac{1}{3}$ and the particles fly apart in the opposite direction with equal velocities.

C

$\frac{m_{1}}{m_{2}} = \frac{2}{1}$ and the collision angle between the particles is $60^{\circ}$ symmetrically.

D

$\frac{m_{1}}{m_{2}} = \frac{2}{1}$ and the particles fly apart symmetrically at an angle $90^{\circ}$

Text Solution

Verified by Experts

The correct Answer is:B, C

$m_{1} u + 0 = - m_{1} v + m_{2} v$ ……….(1)
From kinetic energy conservation
$\frac{1}{2} m_{1} u^{2} = \frac{1}{2} m_{1} v^{2} + \frac{1}{2} m_{2} v^{2}$ ………..(2)

From eq. (1) and and eq. (2) we get , $\frac{m_{1}}{m_{2}} = \frac{1}{3}$
So, choice (b) is correct.
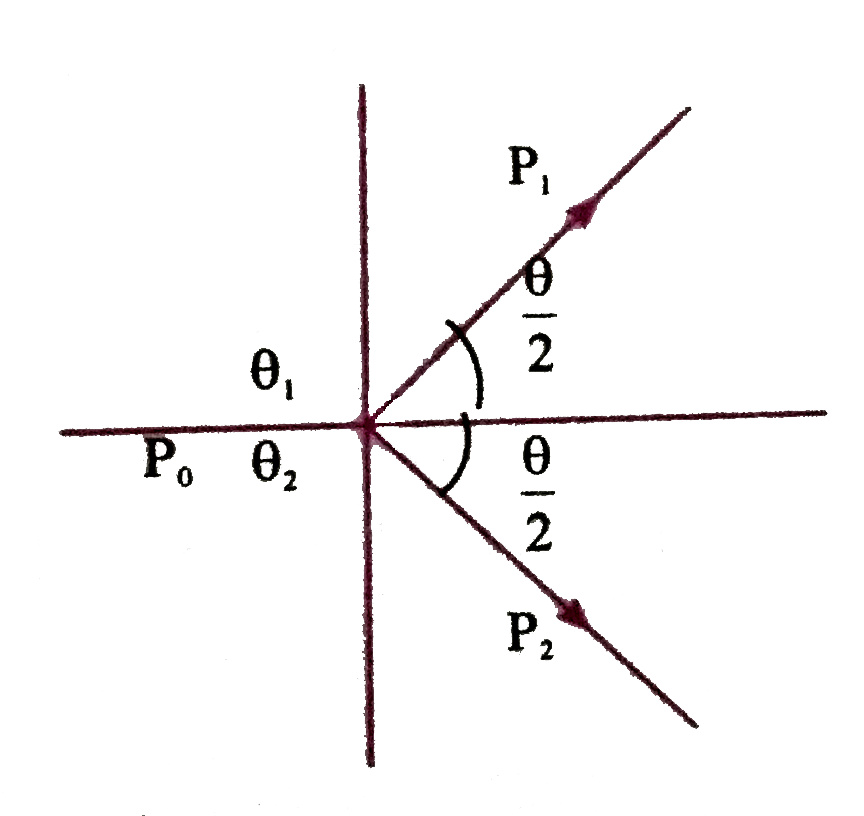
$P^{2} = P_{1}^{2} + P_{2}^{2} + 2 P_{1} P_{2} cos θ$ .........(1)
Also from conservation of kinetic energy
$\frac{P^{2}}{2 m_{1}} = \frac{P_{1}^{2}}{2 m_{1}} + \frac{P_{2}^{2}}{2 m_{2}}$ ............(2)
Since particles fly symmetrically
$P_{1} sin (theta)/(2) = P_(2) sin \frac{θ}{2}$ ..........(3)
Solving eq. (1), (2) and (3) we get
$\frac{m_{1}}{m_{2}} = \frac{2}{1}$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass $m_{1}$ makes an elastic, one-dimensional collision with a stationary particle of mass $m_{2}$ .What fraction of the kinetic energy of $m_{1}$ is carried away by $m_{2}$ ?
A $\frac{m_{1}}{m_{2}}$
B $\frac{m_{2}}{m_{1}}$
C $\frac{2 m_{1} m_{2}}{{(m_{1} + m_{2})}_{1}^{2}}$
D $\frac{4 m_{1} m_{2}}{{(m_{1} + m_{2})}_{1}^{2}}$
Question 2 - Select One
A particle of mass $m_{1}$ makes an elastic one dimensional collision with a stationary particle of mass $m_{2}$ .What fraction of the kinetic energy of $m_{1}$ is carried away by $m_{2}$ ?
A $\frac{m_{1}}{m_{2}}$
B $\frac{m_{2}}{m_{1}}$
C $\frac{2 m_{1} m_{2}}{{(m_{1} + m_{2})}_{1}^{2}}$
D $\frac{4 m_{1} m_{2}}{{(m_{1} + m_{2})}_{1}^{2}}$
Question 3 - Select One
A ball of mass $m_{1}$ makes an elastic , one-dimensional collision with a stationary particle of mass $m_{2}$ . The fraction of the kinetic energy of $m_{1}$ transferred to $m_{2}$ is
A $\frac{2 m_{1} m_{2}}{{(m_{1} + m_{2})}_{1}^{2}}$
B $\frac{4 m_{1} m_{2}}{{(m_{1} + m_{2})}_{1}^{2}}$
C $\frac{m_{1} m_{2}}{{(m_{1} + m_{2})}_{1}^{2}}$
D $\frac{1}{2} \frac{m_{1} 2 m_{2}}{{(m_{1} + m_{2})}_{1}^{2}}$

NARAYNA-COLLISION-Multiple Answer

Home
Ask Doubt
Profile