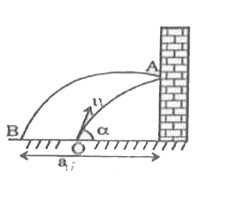
An inelastic ball is projetced with a velocity $' u'$ at an angle $' α'$ to the horizontal, towards a wall distant $' d'$ from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is $' e'$ )

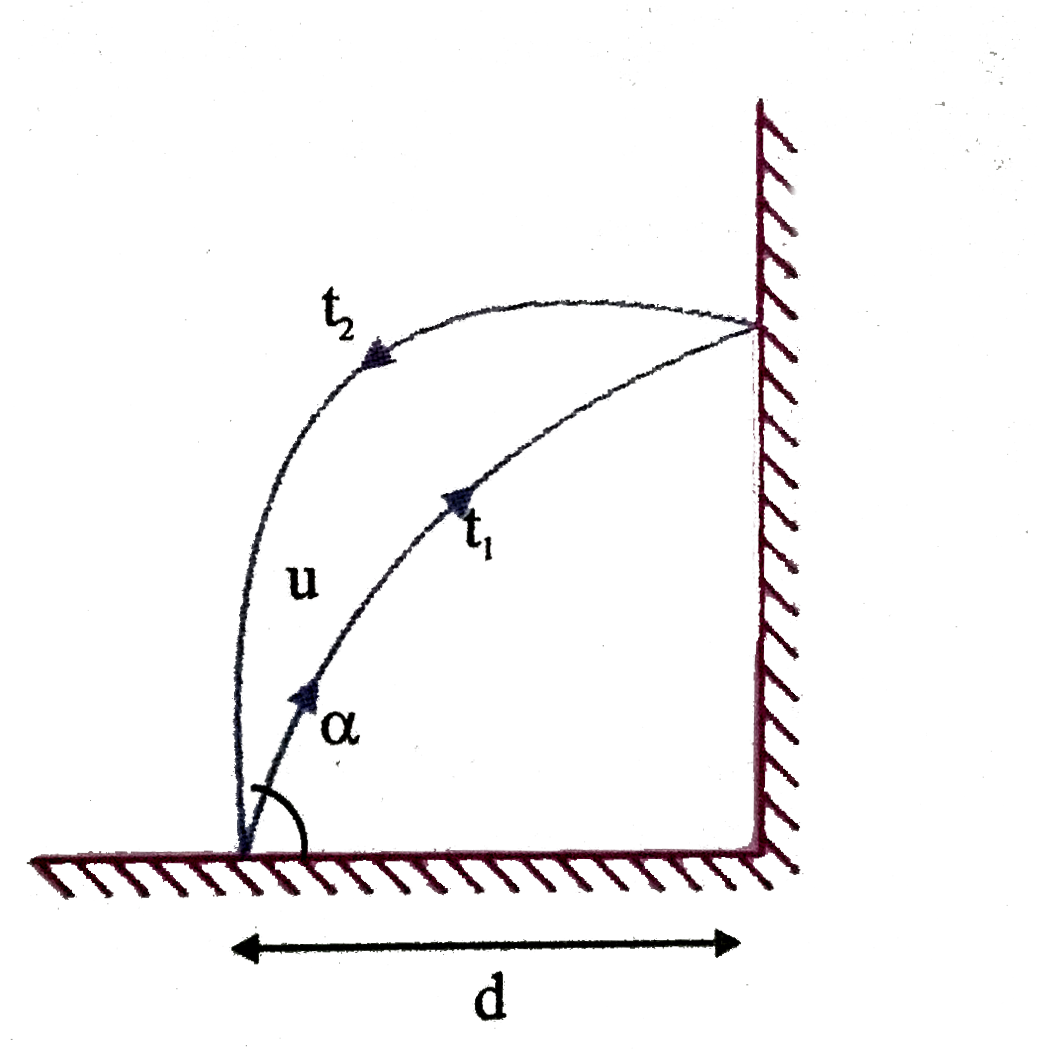
If the line joining the point of projection and the point of impact makes an angle $' θ'$ with the horizontal, then $tan θ$ is

A

$e tan α$

B

$(1 + e) tan α$

C

$\frac{(1 + e)}{tan α}$

D

$\frac{tan α}{(1 + e)}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Time taken ro reach the wall $(t_{1}) \approx \frac{d}{u cos α}$
Time taken to return to the point of projection after impact $(t_{2}) = \frac{d}{e u cos α}$ .
Total time of flight $(T) = t_{1} + t_{2} = \frac{d}{u cos α} (\frac{1 + e}{e})$
There is no change in the vertical component of the velocity after impact
$∴ T = \frac{2 u sin α}{g}$ .........(1)
$\frac{d}{u cos α} (\frac{1 + e}{e}) = \frac{2 u sin α}{g}$
$d = \frac{u^{2} sin 2 α}{g} (\frac{e}{1 + e}) ... ... ... (2)$
From Fig. $Tan θ = \frac{y}{d}, y = d tan θ$
$y = (tan α) x - \frac{1}{2} \frac{g}{u^{2} {cos}^{2} α} \times x^{2}$
$(tan θ) d = (tan α) d - \frac{1}{2} \frac{g}{u^{2} {cos}^{2} α} \times d^{2}$
$tan θ = tan α - \frac{1}{2} \frac{g}{u^{2} {cos}^{2} α} \times d$ .......(3)
From (2) and (3)
$tan θ = \frac{tan α}{1 + e}$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An inelastic ball is projetced with a velocity $' u'$ at an angle $' α'$ to the horizontal, towards a wall distant $' d'$ from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is $' e'$ )

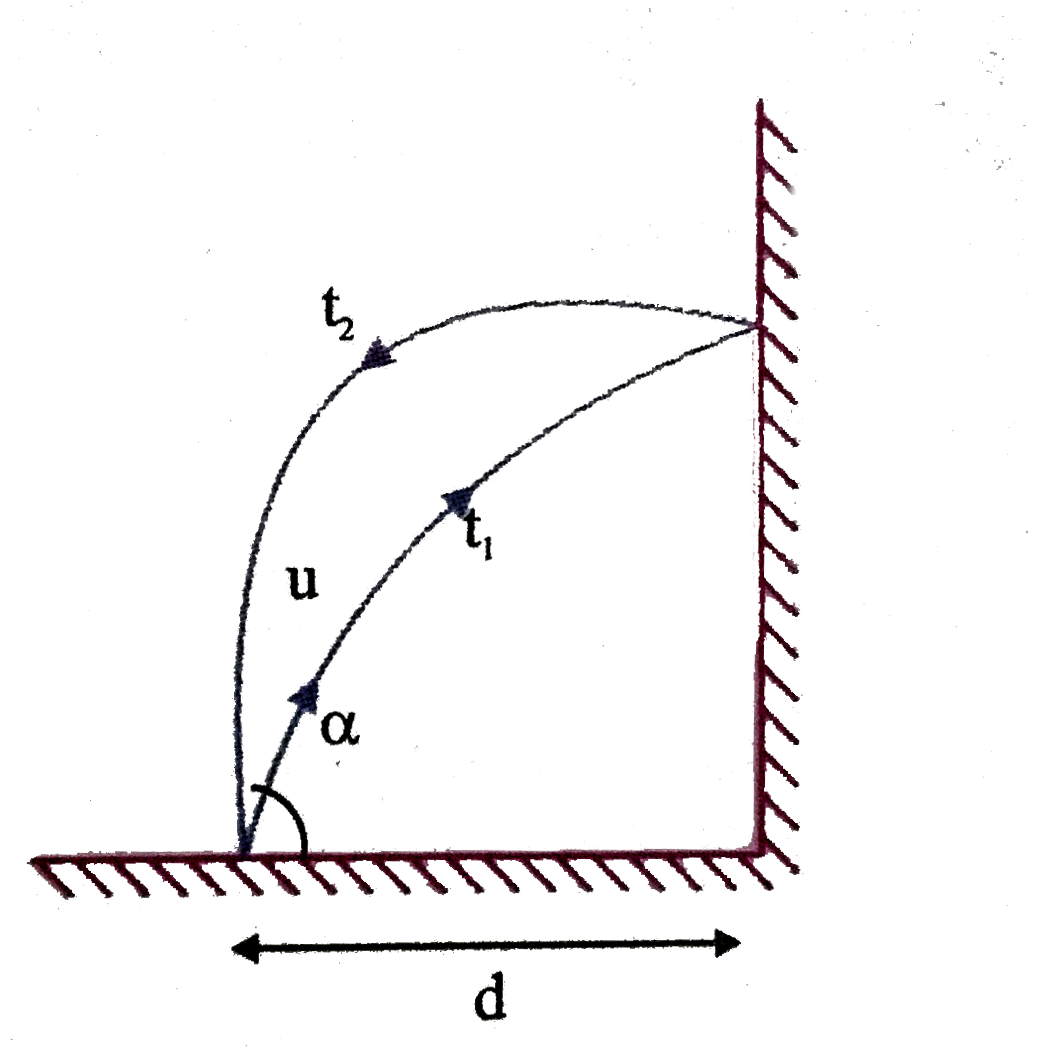
The total time of journey of the ball is
A $\frac{u sin α}{g}$
B $\frac{2 u sin α}{g}$
C $\frac{2 u cos α}{g}$
D $\frac{u tan α}{2 g}$
Question 2 - Select One
An inelastic ball is projetced with a velocity $' u'$ at an angle $' α'$ to the horizontal, towards a wall distant $' d'$ from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is $' e'$ )

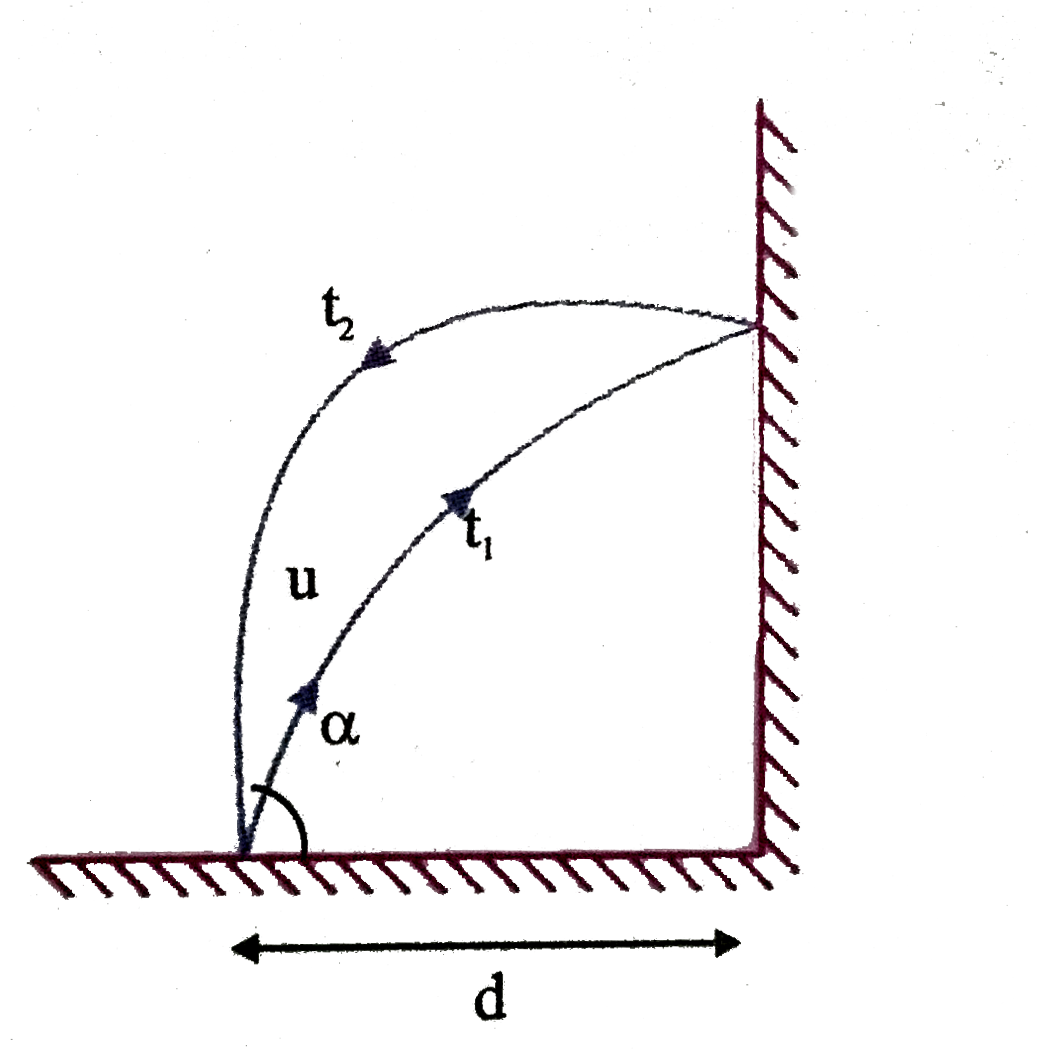
The horizontal distance $' d'$ from the wall is
A $\frac{u^{2} sin 2 α}{g} (\frac{e}{1 + e})$
B $\frac{u^{2} sin α}{g} (\frac{e}{1 + e})$
C $\frac{u^{2} cos 2 α}{g} (\frac{e}{1 + e})$
D $\frac{u^{2} sin 2 α}{2 g} (\frac{e}{1 + e})$
Question 3 - Select One
A particle is projected with velocity v at an angle $θ$ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
A $\frac{g cos θ}{θ v}$
B $\frac{g}{v sin θ}$
C $\frac{g}{v θ}$
D $\frac{g θ}{v sin θ}$

NARAYNA-COLLISION-Comprehension type

Home
Ask Doubt
Profile