A bucket of mass 'm' tied to a light rope is lowered at a constant acceleration of g/4. IF the bucket is lowered by a distance 'd' , the work done by the rope will be (neglect the mass of the rope)
14mgd
34mgd
−34mgd
−54mgd
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Identify the forces acting on the bucket
The forces acting on the bucket are:
1. The gravitational force (weight) acting downward, which is mg.
2. The tension force T in the rope acting upward.
Step 2: Apply Newton's second law
Since the bucket is being lowered with a constant acceleration of g4, we can use Newton's second law:
Fnet=ma
Here, the net force acting on the bucket is the difference between the gravitational force and the tension:
mg−T=m(g4)
Step 3: Solve for the tension T
Rearranging the equation gives:
T=mg−m(g4)
T=mg−mg4
T=4mg4−mg4=3mg4
Step 4: Calculate the work done by the rope
The work done by the tension in the rope when the bucket is lowered by a distance d can be calculated using the formula:
W=F⋅d⋅cos(θ)
Where:
- F is the tension T=3mg4,
- d is the distance lowered,
- θ is the angle between the force and the displacement. Since the tension acts upward and the displacement is downward, θ=180∘.
Thus, cos(180∘)=−1:
W=(3mg4)⋅d⋅(−1)
W=−3mgd4
Final Answer
The work done by the rope when the bucket is lowered by a distance d is:
W=−3mgd4
---
The forces acting on the bucket are:
1. The gravitational force (weight) acting downward, which is mg.
2. The tension force T in the rope acting upward.
Since the bucket is being lowered with a constant acceleration of g4, we can use Newton's second law:
Fnet=ma
Here, the net force acting on the bucket is the difference between the gravitational force and the tension:
mg−T=m(g4)
Rearranging the equation gives:
T=mg−m(g4)
T=mg−mg4
T=4mg4−mg4=3mg4
The work done by the tension in the rope when the bucket is lowered by a distance d can be calculated using the formula:
W=F⋅d⋅cos(θ)
Where:
- F is the tension T=3mg4,
- d is the distance lowered,
- θ is the angle between the force and the displacement. Since the tension acts upward and the displacement is downward, θ=180∘.
W=(3mg4)⋅d⋅(−1)
W=−3mgd4
The work done by the rope when the bucket is lowered by a distance d is:
W=−3mgd4
Topper's Solved these Questions
Similar Questions
A bucket tied to a string is lowered at a constant acceleration of g/4. If mass of the bucket is m and it is lowered by a distance /then find then work done by the string on the bucket.
View SolutionA bucket of mass 4/3 is tied to a string and is lowered at a constant acceleration of g/4. The magnitude of work done (in joule ) by the string in lowering the bucket by 10cm would be :
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m tied to a string is lowered by a distance d, at a constant acceleration of g/3. The work done by the string is
Amgd3B−mgd3C23mgdD−23mgd - Question 2 - Select One
A mass M is lowered with the help of a string by a distance h at a distance acceleration g/2. The work done by the string will be
A(a) Mgh2B(b) −Mgh2C(c) 3Mgh2D(d) −3Mgh2 - Question 3 - Select One
A mass M is lowered with the help of a string by a distance h at a distance acceleration g/2. The work done by the string will be
AMgh2B−Mgh2C3Mgh2D−Mgh2
A block of 'm' is lowered with the help of a rope of negligible mass through a distance 'd' with an acceleration of g/3. Find the work done by the rope on the block ?
View SolutionA cord is used to lower vertically a block of mass M through a distance d at a constant acceleration g/4. Find the work done by the cord on the block.
View SolutionA cord is used to lower vertically a block of mass M, a distance d at a constant downward acceleration of g4, then the work done by the cord on the block is
View SolutionA bus is moving with a constant acceleration a=3g/4 towards right. In the bus, a ball is tied with a rope and is rotated in vertical circle as shown. The tension in the rope will be minimum, when the rope makes an angle θ=_____
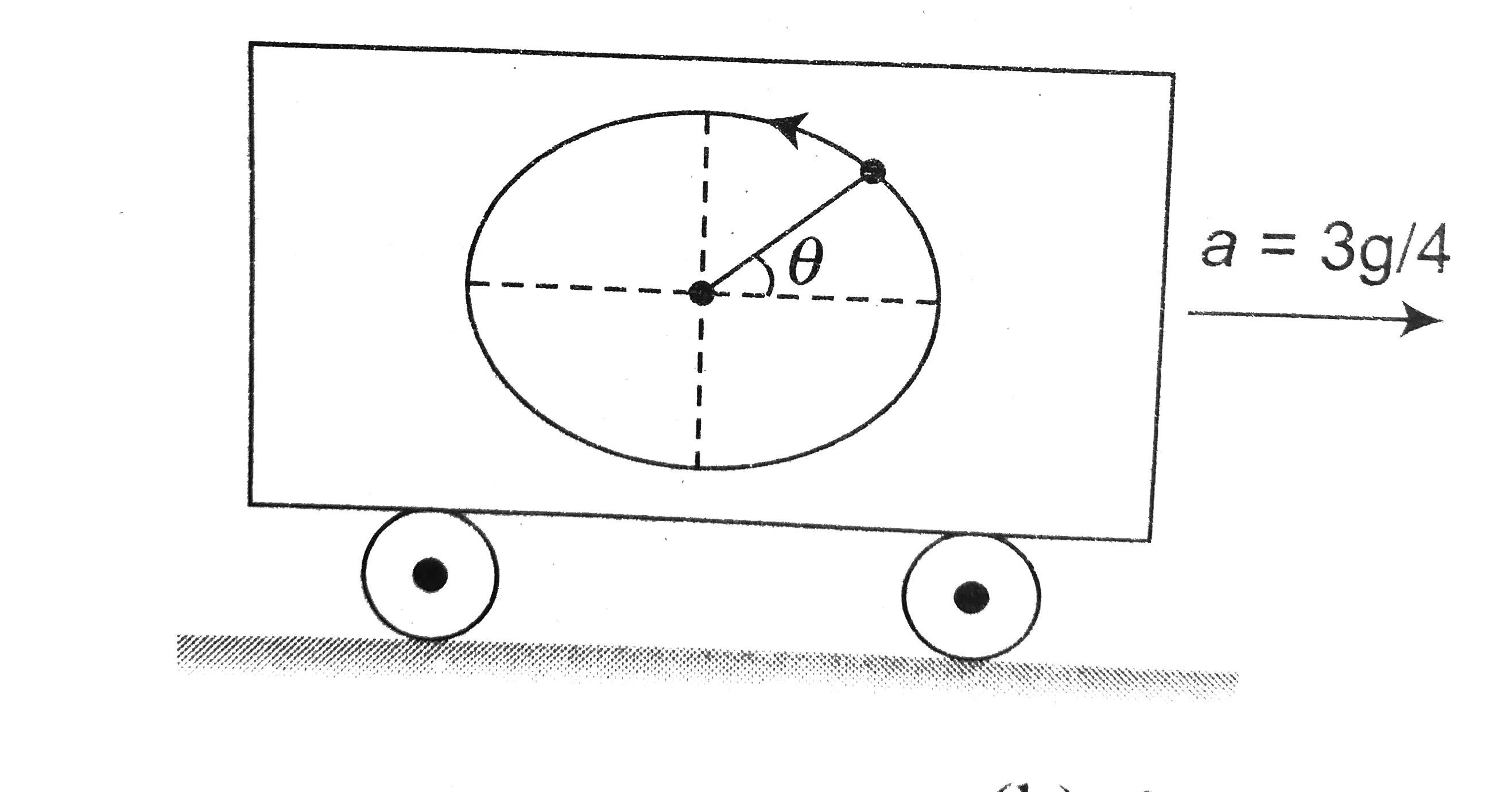 View Solution
View SolutionA 20 kg monkey slides down a vertical rope with a constant acceleration of 7ms−2. If g=10m/s−2, what is the tension in the rope ?
View Solution

