A magnet of magnetic is in the form of a quadrant of a circle. If it is strightened, its new magnetic moment will be
The correct Answer is:D
To solve the problem of finding the new magnetic moment of a magnet that was initially in the form of a quadrant of a circle and then straightened, we can follow these steps:
1. Understand the Initial Configuration:
- The magnet is in the shape of a quadrant of a circle.
- Let's denote the radius of the circle as R.
2. Calculate the Length of the Magnet:
- The length L of the arc of the quadrant can be calculated as:
L=14×2πR=πR2
3. Determine the Distance Between the Poles:
- The distance between the north and south poles of the magnet, which are located at the ends of the radius, is given by:
d=R√2
- This is derived from the Pythagorean theorem since the two radii form a right triangle.
4. Calculate the Initial Magnetic Moment:
- The magnetic moment M of the magnet can be expressed as:
M=(Pole Strength)×d=(Pole Strength)×(R√2)
- Let the pole strength be denoted as m. Thus, we have:
M=m⋅R√2
5. Express Radius in Terms of Length:
- From the earlier expression for L:
R=2Lπ
6. Substitute R into the Magnetic Moment:
- Substitute R into the expression for M:
M=m⋅(2Lπ)√2=2mL√2π
7. Straighten the Magnet:
- When the magnet is straightened, its new length becomes L, and the distance between the poles remains L.
- The new magnetic moment M′ can be expressed as:
M′=(Pole Strength)×L=m⋅L
8. Relate the New Magnetic Moment to the Old One:
- From the earlier expression for m:
m=Mπ2L√2
- Substitute m back into the expression for M′:
M′=(Mπ2L√2)⋅L=Mπ2√2
9. Final Expression for the New Magnetic Moment:
- Therefore, the new magnetic moment M′ is given by:
M′=Mπ2√2
Conclusion:
The new magnetic moment when the magnet is straightened is:
M′=Mπ2√2
- The magnet is in the shape of a quadrant of a circle.
- Let's denote the radius of the circle as R.
- The length L of the arc of the quadrant can be calculated as:
L=14×2πR=πR2
- The distance between the north and south poles of the magnet, which are located at the ends of the radius, is given by:
d=R√2
- This is derived from the Pythagorean theorem since the two radii form a right triangle.
- The magnetic moment M of the magnet can be expressed as:
M=(Pole Strength)×d=(Pole Strength)×(R√2)
- Let the pole strength be denoted as m. Thus, we have:
M=m⋅R√2
- From the earlier expression for L:
R=2Lπ
- Substitute R into the expression for M:
M=m⋅(2Lπ)√2=2mL√2π
- When the magnet is straightened, its new length becomes L, and the distance between the poles remains L.
- The new magnetic moment M′ can be expressed as:
M′=(Pole Strength)×L=m⋅L
- From the earlier expression for m:
m=Mπ2L√2
- Substitute m back into the expression for M′:
M′=(Mπ2L√2)⋅L=Mπ2√2
- Therefore, the new magnetic moment M′ is given by:
M′=Mπ2√2
The new magnetic moment when the magnet is straightened is:
M′=Mπ2√2
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MAGNETISMEXERCISE - LEVEL-II (H.W)24videos
MAGNETISM
- BOOK - NARAYNACHAPTER - MAGNETISMEXERCISE - NCERT Based Questions17videos
MAGNETISM
- BOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type6videos
EXPERIMENTAL PHYSICS
- BOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)17videos
MAGNETISM AND MATTER
Similar Questions
A bar magnet of length and magnetic dipole moment 'M' is bent in the form of an arc as shown in figure. The new magnetic dipole moment will be
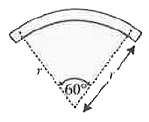 View Solution
View SolutionA bar magnet of lenth l and magnetic dipole moment 'M' is bent in the form of an arc as shown in figure. The new magnetic dipole moment will be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A bar magnet of magnetic moment M is bent in the form of quadrant of circular arc . The new magnetic moment is
A2MπB2√2MπC√2MπDM - Question 2 - Select One
A bar magnet of moment 'M' is bent into a shape
 . If the length of the each part is same, its new magnetic moment will be AM√3BM√5CM√2D23M
. If the length of the each part is same, its new magnetic moment will be AM√3BM√5CM√2D23M - Question 3 - Select One
A bar magnet of moment 'M' is bent into a shape '5'. If the length of the each part is same, its new magnetic moment will be
AM√3BM√5CM√2D23M
A bar magnet of l length and magnetic dipole moment M is bent in the form of an arc as shown in the figure. The new magnetic dipole moment will be
 View Solution
View SolutionA magnetised wire of magnetic moment 'M' and length 'l' is bent in the form of a semicircle of radius 'r'. The new magnetic moment is
View SolutionAn iron rod of length L and magnetic moment M is bent in the form of a semicircle. Now its magnetic moment will be
View SolutionIf a hole is made at the centre of a bar magnet, then its magnetic moment will
View SolutionA bar magnet of length l and magnet dipole moment M is bent in the form of an arc. The new magnetic dipole moment is
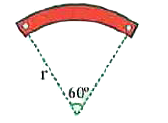 View Solution
View Solution

