How many half-lives are needed to complete the zeroth order reaction ?
A
Two
B
Four
C
Infinite
D
Eight
Video Solution
Text Solution
The correct Answer is:A
The half-life of a reaction, symbolized by t1/2 , is the time required for the reactant concentration to drop to one half of its intial value.
Suppose a zero order reaction of the from
a0 initial concentration
A→B
(a−x)x concentration at time t
Integrated rate law is
K0=xt
where K0 is the rate constantl of a zero order reaction. When t=t1/2 , half of the reatant is converted into product. thus x=a/2 . Using integrated rate law, we can write
t1/2=a2K
Multiplying both sides by 2 , we get
2t1/2=aK=t∞
where t∞ is the time taken for the completion of the reaction. Thus, two half lives are required to complete the zero order reaction.
For first order reaction, the integrated rate law is
t=2.303klog(aa−x)
Substituting the value of K in terms of half-life we get
t=2.3030.693/t1/2log(aa−x)
When reaction is complete, t=t∞ and x=a . Therefore
t∞=2.303t1/20.693log(aa−a)
=2.3030.693t1/2log(a0)
=2.3030.693t1/2(∞)
Therefore, infinite half lives are needed to complete a first order reaction.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - R SHARMACHAPTER - CHEMICAL KINETICSEXERCISE - Follow-up 512videos
CHEMICAL KINETICS
- BOOK - R SHARMACHAPTER - CHEMICAL KINETICSEXERCISE - Follow-up 62videos
CHEMICAL KINETICS
- BOOK - R SHARMACHAPTER - CHEMICAL KINETICSEXERCISE - Follow-up 310videos
CHEMICAL KINETICS
- BOOK - R SHARMACHAPTER - BIOMOLECULESEXERCISE - Archives47videos
BIOMOLECULES
- BOOK - R SHARMACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - Archives11videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
Knowledge Check
- Question 1 - Select One
Two persons can complete a piece of work in 9 days. How many more persons are needed to complete double the work in 12 days?
A3B2C4D1 - Question 2 - Select One
Two persons can complete a piece of work in 9 days. How many more persons are needed to complete double the work in 12 days?
A3B2C4D1 - Question 3 - Select One
Which is not the graphical representation for the zeroth order reaction ?
A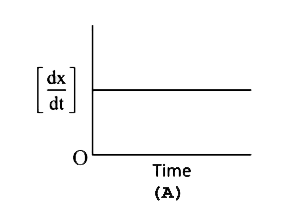 B
B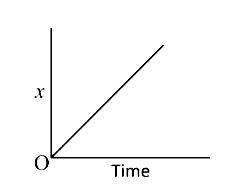 C
C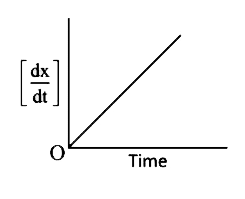 D
D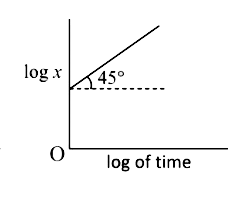
For a first order reaction, calculate the ratio between the time taken to complete three fourth of the reaction and the time taken to complete half of the reaction.
View SolutionHow many times of the half-life will require to complete 75% of a reaction of first order?
View SolutionHow many moles of BH3 are needed to react completely with 2 mole of 1-pentene in hydroboration-oxidation reaction?
View SolutionAt least how many half-lives should elapse for a 1st order reaction A→ products so that the reaction is at least 95% completed?
(log2=0.3)View SolutionA first order reaction is half completed in 45 minutes. How long does it need 99.9% of the reaction to be completed
View Solution

