If l,m,n are lines in the same plane such that l intersects m and n∣∣m then n intersects l also
To prove that if lines l,m,n are in the same plane such that l intersects m and n is parallel to m, then n must also intersect l, we will use a proof by contradiction.
1. Understand the Given Information:
- We have three lines: l, m, and n.
- Line l intersects line m.
- Line n is parallel to line m (denoted as n∥m).
2. Assume the Opposite:
- To use the method of contradiction, we will assume that line n does not intersect line l.
3. Implication of the Assumption:
- If n does not intersect l, then by definition of parallel lines, it implies that l is parallel to n (denoted as l∥n).
4. Analyze the Relationships:
- We now have two relationships:
- l∥n
- n∥m
5. Conclude from the Relationships:
- If l∥n and n∥m, then by the transitive property of parallel lines, it follows that l∥m.
6. Contradiction:
- However, this contradicts our initial condition that l intersects m. If l intersects m, then they cannot be parallel.
7. Conclusion:
- Since our assumption that n does not intersect l leads to a contradiction, we conclude that our assumption is false. Therefore, line n must intersect line l.
Final Statement:
Thus, we have proved that if l intersects m and n∥m, then n must also intersect l.
- We have three lines: l, m, and n.
- Line l intersects line m.
- Line n is parallel to line m (denoted as n∥m).
- To use the method of contradiction, we will assume that line n does not intersect line l.
- If n does not intersect l, then by definition of parallel lines, it implies that l is parallel to n (denoted as l∥n).
- We now have two relationships:
- l∥n
- n∥m
- If l∥n and n∥m, then by the transitive property of parallel lines, it follows that l∥m.
- However, this contradicts our initial condition that l intersects m. If l intersects m, then they cannot be parallel.
- Since our assumption that n does not intersect l leads to a contradiction, we conclude that our assumption is false. Therefore, line n must intersect line l.
Thus, we have proved that if l intersects m and n∥m, then n must also intersect l.
Similar Questions
Knowledge Check
If l, m, n are the direction consines of a line, then
Al+m+n=0Bl+m+n=1Cl2+m2+n2=1Dl2+m2+n2=0If l,m,n are direction cosines of the line then −l,−m,−n can be
Aonly direction ratios of the lineBonly direction cosines of the lineCdirection cosines and direction ratios of the lineDneither direction cosines nor direction ratios of the lineIf l,m,nandl',m',n' be the direction cosines of two lines which include an angle θ, then
Acosθ=ll'+mm'+nn'Bsinθ=ll'+mm'+nn'Ccosθ=mn'+m'n+nl'+n'l+lm'+l'mDsinθ=mn'+m'n+nl'+n'l+lm'+l'm
If l,m,n are three lines such that l∣∣m and n⊥l, prove that n⊥m.
View Solutionl, m and n are three parallel lines intersected by transversals p and q such that l, mand n cut off equal intercepts AB and BC on p (see Fig. 8.28). Show that l, m and n cut off equal intercepts DE and EF on q also
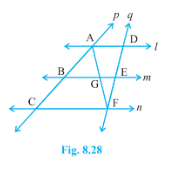
View SolutionTwo lines l and m interset at the O and P is Point on a line n Passing through the point O such that P is equidistant from l and m. Prove that n is the bisectof the angle formed by l and m
View SolutionThe direction cosines l, m and n of two lines are connected by the relations l+m+n=0andlm=0, then the angle between the lines is
View SolutionIn the figure , l||m & l||n then x is -
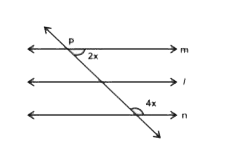
View Solution
