Surface area of Spherical Shell
Step by step video & image solution for Surface area of Spherical Shell by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
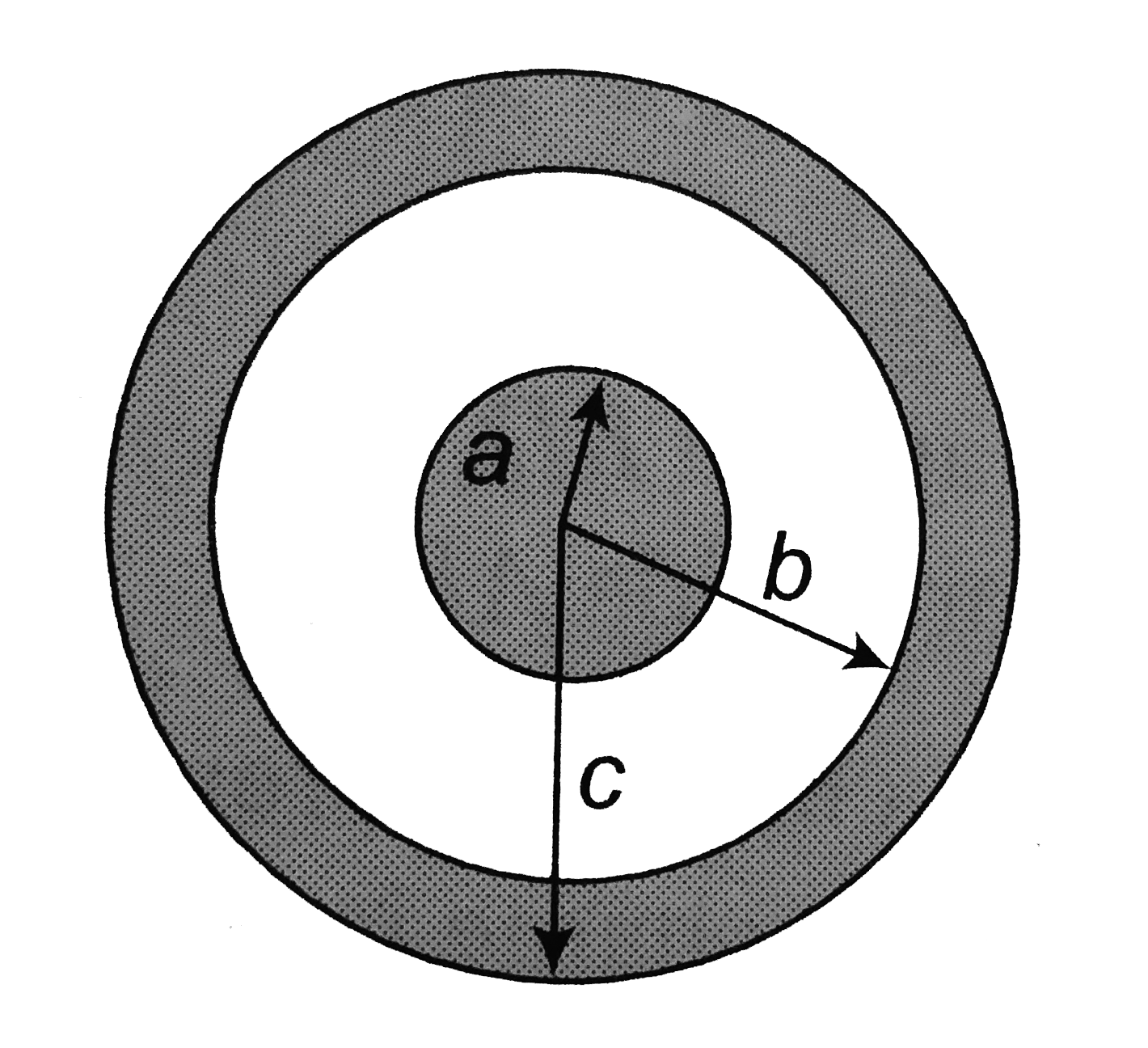 A−2Q4πb2,Q4πc2B−Q4πb2,Q4πc2C0,Q4πc2DNone of the above
A−2Q4πb2,Q4πc2B−Q4πb2,Q4πc2C0,Q4πc2DNone of the aboveA positive charge Q is placed at the centre O of a thin metalic spherical shell. Select the correct statements from the following:
(i) The electric field at any point outside the shell is zero
(ii) The electrostatic potential at any point outside the shell is Q4πε0r , where r is the distance of the point from O
(iii) The outer surface of the spherical shell is an equipotential surface
(iv) The electric field at any point inside the shell , other than O , is zeroA(i),(ii)B(ii),(iii)C(i),(iv)DallA conducting sphere carries a net charge of −6μC. The sphere is located at the center of a conducting spherical shell that carries a net charge of +2μC as shown in the figure. Determine the excess charge on the outer surface of the spherical shell.
 A−4μCB+4μCC−8μCD+8μC
A−4μCB+4μCC−8μCD+8μC
A spherical shell is kept in an atmosphere at temperature T0. The wavelength corresponding to maximum intensity of radiation for the shell is λ0. A point source of constant power is switched on inside the shell. The power radiated by the source is P=04σSeT40 where S, e and σ are outer surface area of the shell, emissivity of the outer surface of the shell and Stefan’s constant respectively. Calculate the new wavelength (λ) corresponding to the maximum intensity of radiation from the shell. Assume that change in temperature (ΔT) of the shell is small compared to the ambient temperature T0.
View SolutionThe outer diameter of a spherical shell is 12 cm and its inner diameter is 8 cm. Find the volume of metal contained in the shell. Also, find its outer surface area.
View SolutionA particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.

View SolutionA body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
View SolutionShown in the figure a spherical shell with an inner radius 'a' and an outer radius 'b' is made of conducting metarial. A charge +Q is placed at the centre of the spherical shell and a total charge -q s placed on the shell. Charge -q is districuted on the surfaces as :

View Solution
