There are three concentric metallic spherical shells of radius R, 2R and 3R. Charge Q is given to the innermost spherical shell. If the innermost spherical shell is connected with a metal wire to the outermost spherical shell without touching the middle shell, which is connected to the earth, then, find charges appearing on all surfaces.
If we read the question carefully then we get to know that charge distribution is to be done in a way that net charge outermost spheres together is Q, and electric potential of middle sphere is equal to zero because it is connected to the earth.

Let us start with the innermost sphere. There should not be any charge on inner surface of this sphere because there is no electric field inside it. Let us assume that q1 charge appears on outer surface of the innermost sphere then we know that charge on inner surface of middle sphere of has to be −q1 due to electrical constraint of metallic surfaces facing each other. Now we know that the middle sphere is connected to the earth. Hence, it is not isolated. Let us assume that q2 charge appears on the outer surface of the middle sphere, then again due to electrical constraint charge on inner surface of outermost sphere has to be −q2. Now charge on the outer surface of the outermost sphere is (Q−q1+q2) so that the total charge on innermost and outermost spheres together remains Q.
Electric potential of the innermost sphere is equal to the outermost sphere because the two are connected to each other by a metallic wire so charge on them must ensure same potential on them. We get the following equation:
Vinner-most=Vouter-most
q14πε0(R)+q2−q14πε0(2R)+Q−q14πε0(3R)
=q14πε0(3R)+q2−q14πε0(3R)+Q−q14πε0(3R)
⇒6q1+3q2−3q1=2q1+2q2−2q1
⇒3q1=−q2⇒q1=−q23 ...(i)
The middle sphere is earthed and hence its electrical potential is zero. We get the following equation:
Vmiddle-sphere=q14πε0(2R)+q2−q1rπε0(2R)+Q−q14πε0(3R)=0
⇒q24πε0(2R)+Q−q14πε0(3R)=0
⇒3q2+2Q−2q1=0
⇒2q1−3q2=2Q ...(ii)
Now substituting value of q1 from equation (ii) we get the following:
⇒2(−q23)−3q2=2Q⇒2q23+2q2=−2Q
⇒113q2=−2Q⇒q2=−611Q ...(iii)
Substituting value of q2 from equation (iii) in equation (i) we get the following:
⇒q1=211Q ...(iv)
Now the charge on outer surface of the outermost sphere can be written as: Q−q1+q2
Q−q1+q2=Q−211Q−611Q=3Q11.
Now we have charges on all surfaces.
Charge on inner surface of the innermost sphere: 0
Charge on outer surface of the innermost sphere: 2Q/11
Charge on inner surface of the middle sphere: −2Q/11
Charge on outer surface of the middle sphere: −6Q/11
Charge on inner surface of the outermost sphere: 6Q/11
Charge on outer surface of the outermost sphere: 3Q/11
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Textbook Exercise)
11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Additional Exercises)
23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Conceptual Questions
37 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Two concentric metallic spherical shells are given positive charges . Then
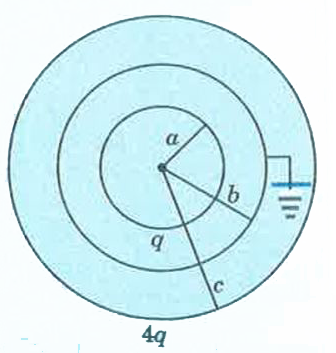
View SolutionThere are three concentric metallic spherical shells of radius a, b and c respectively as shown in the figure. The innermost sphere is given a charge q and the outermost sphere is given a charge 4q while the middle sphere is earthed. Find the charges appearing on the inner and outer surfaces of middle sphere.
View Solution
Knowledge Check
Two concentric metallic spherical shells are given positive charges then
Amore than that of the first conductorBless than that of first conductorCequal to that of first conductorDuncertainTwo concentric metallic spherical shells are given positive charges . Then
Athe outer sphere is always at a higher potentialBthe inner sphere is always at a higher potentialCboth the spheres are at the same potentialDno prediction can be made about their potentials unless the actual values of charges and radii are knownThere are three concentric metallic spherical shells of radii R, 2R and 3q, respectively. The middle spherical shell is connected to earth. Let q1 be the charge appearing on the inner surface of the middle sphere and q2 be the charge on outer surface of the middle sphere. Similarly q3 is the charge appearing on inner surface of outermost sphere and q4 is the charge appearing on outer surface of outermost sphere.
 APQRS4312BPQRS4321CPQRS3412DPQRS3421
APQRS4312BPQRS4321CPQRS3412DPQRS3421
There are two concentric spherical shell of radii r and 2r. Initially, a charge Q is given to the inner shell and both the switches are open.

If switch S1 is closed and then opened, charge on the outer shell will be
View SolutionThere are three concentric conducting spherical shells. All of them are charged. The innermost sphere is connected by a conducting wire to the outermost sphere. Prove that the final charge on the innermost sphere is independent of the initial charge of outermost sphere.
View SolutionThere are three concentric conducting spherical shells. All of them are charged. The innermost sphere is connected by a conducting wire to the outermost sphere. Prove that the final charge on the innermost sphere is independent of the initial charge of outermost sphere.
View SolutionA spherical shell of radius R has a charge +q units. The electric field due to the shell at a point
View SolutionThere are two concentric spherical shell of radii r and 2r. Initially, a charge Q is given to the inner shell and both the switches are open.

If switch S1 is closed and then opened, charge on the outer shell will be
View Solution
