The internal angle bisector of an angle of a triangle divide the opposite side internally in the ratio of the sides containgthe angle
Step by step video & image solution for The internal angle bisector of an angle of a triangle divide the opposite side internally in the ratio of the sides containgthe angle by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Read the statemenst carefully and state 'T' for true and 'F' for false .
1. If a line divides any two sides of a triangle in the same ratio , then the line is parallel to the third side of the triangle .
2 . The internal bisector of an angle of a triangle divides the opposite side inernally in the ratio of the sides containing the angle .
3 . If a line through one vertex of a triangle divides the opposite in the ratio of other two sides , then the line bisects the angle at the vertex .
4.Any line parallel to the parallel sides dividesproportionally .
5. Two times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle .A12345TTTTTB12345TTTTFC12345FTFTFD12345TTFTFThe internal /external bisector of an angled of a triangle divides the opposite side internally / externally in the ratio of the sides containing the angle .
In the given figure ,Ae is the bisector of the exterior ∠CAD meeting BC produced in E . If AB=15 cm , AC = 8 cm and BC =14 cm , find CE .
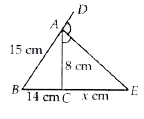 A12 cmB16 cmC20 cmD18 cm
A12 cmB16 cmC20 cmD18 cmIf angle bisector of a triangle bisect the opposite side, then what type of triangle is it?
ARight angledBScaleneCSimilarDIsosceles
Prove the following statement. "The bisector of an angle of a triangle divides the sides opposite to the angle in the ratio of the remaining sides"
View SolutionIn order to prove, 'The bisector of an angle of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
(i) Draw a neat labelled figure.
(ii) Write 'Given' and 'To prove'.
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIf a line through one vertex of a triangle divides the opposite sides in the Ratio of other two sides; then the line bisects the angle at the vertex.
View SolutionOne angle of a triangle is equal to one angle of another triangle and the bisectors of these two equal angles divide the opposite sides in the same ratio, prove that the triangles are similar.
View Solution
