Question

Prove ${\sin }^2\theta +{\cos }^2\theta =1$

Explanation

To prove the identity $${\sin }^2\theta +{\cos }^2\theta =1$$, we will use the properties of a right-angled triangle and the Pythagorean theorem.

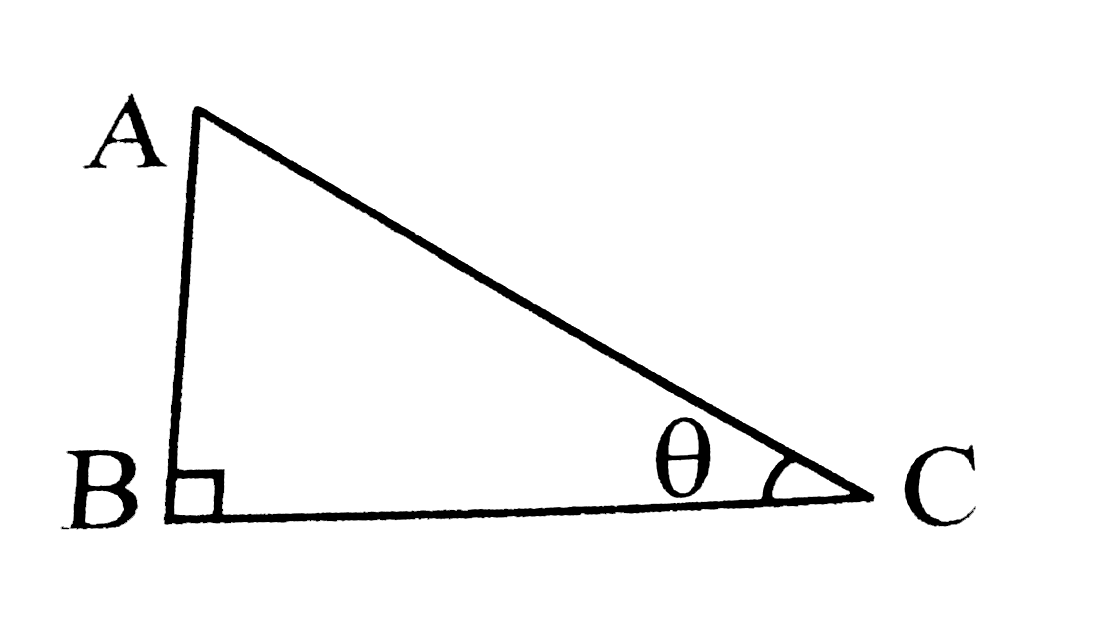
1. Consider a Right-Angled Triangle:
- Let triangle ABC be a right-angled triangle where angle C is \( \theta \), and angle A is \( 90^\circ \).
- In this triangle:
- Side AB is opposite to angle \( \theta \) (let's denote it as \( a \)).
- Side BC is adjacent to angle \( \theta \) (let's denote it as \( b \)).
- Side AC is the hypotenuse (let's denote it as \( c \)).

2. Apply the Pythagorean Theorem:
- According to the Pythagorean theorem, we have:
\( a^2 + b^2 = c^2 \)

3. Express the Sine and Cosine Ratios:
- The definitions of sine and cosine in terms of the sides of the triangle are:
- \( \sin \theta = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{a}{c} \)
- \( \cos \theta = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{b}{c} \)

4. Square the Sine and Cosine Ratios:
- Squaring both sine and cosine gives:
\( \sin^2 \theta = \left(\frac{a}{c}\right)^2 = \frac{a^2}{c^2} \)
\( \cos^2 \theta = \left(\frac{b}{c}\right)^2 = \frac{b^2}{c^2} \)

5. Add the Squared Ratios:
- Now, add \( \sin^2 \theta \) and \( \cos^2 \theta \):
\( \sin^2 \theta + \cos^2 \theta = \frac{a^2}{c^2} + \frac{b^2}{c^2} \)
- This can be combined into a single fraction:
\( \sin^2 \theta + \cos^2 \theta = \frac{a^2 + b^2}{c^2} \)

6. Substitute from the Pythagorean Theorem:
- From the Pythagorean theorem, we know that \( a^2 + b^2 = c^2 \). Substituting this into our equation gives:
\( \sin^2 \theta + \cos^2 \theta = \frac{c^2}{c^2} = 1 \)

7. Conclusion:
- Therefore, we have proved that:
\( \sin^2 \theta + \cos^2 \theta = 1 \)