A partical starts from rest and moves in a straight line. It travels a distance L with uniform acceleration and then moves with constant velocity a further distance $2 L$ . Finally, it comes to rest after moving a further distance 4L under uniform retardation. Find the ratio of average speed to the maximum speed.

Video Solution

Text Solution

Verified by Experts

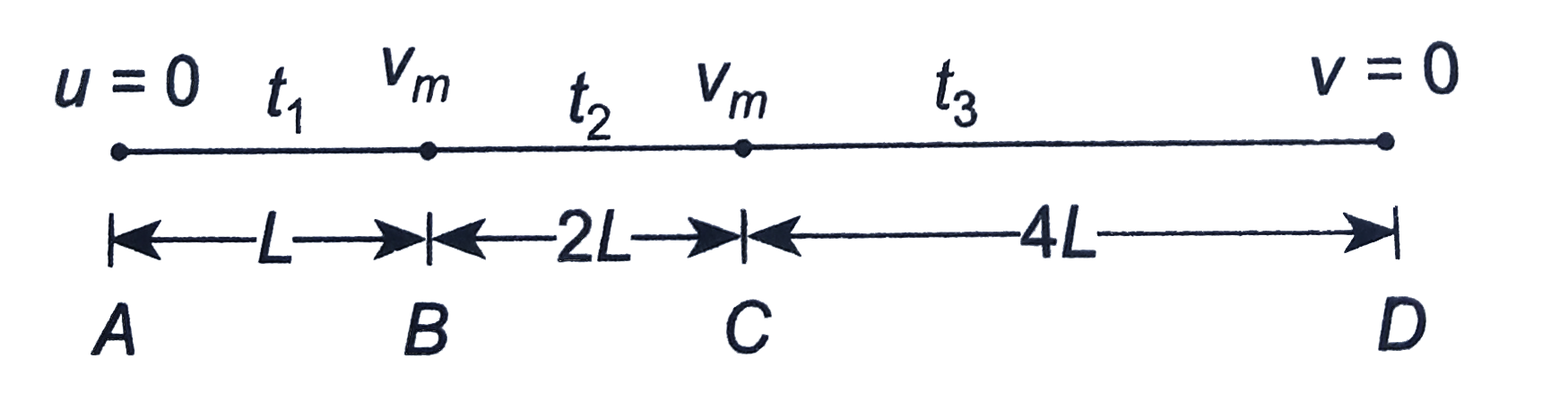
$A$ to $B$ : (constant acceleration)
$L = (\frac{0 + v_{m}}{2}) t_{1} \Rightarrow t_{1} = \frac{2 L}{v_{m}}$
$B$ to $C$ : (constant velocity)
$2 L = v_{m} t_{2} \Rightarrow t_{2} = \frac{2 L}{v_{m}}$
$C$ to $D$ : (constant retardation)
$4 L = (\frac{v_{m} + 0}{2}) t_{3} \Rightarrow t_{3} = \frac{8 L}{v_{m}}$
Total distance= $L + 2 L + 4 L = 7 L$
Total time $= t_{1} + t_{2}_t_{3} = \frac{2 L}{v_{m}} + \frac{2 L}{v_{m}} + \frac{8 L}{v_{m}} = \frac{12 L}{v_{m}}$
Average speed $¯ v = \frac{7 L}{\frac{12 L}{v_{m}}} = \frac{7 v_{m}}{12}$
$\frac{¯ v}{v_{m}} = \frac{7}{12}$

Updated on:21/07/2023

A particle starts from rest and traverses a distance l with uniform acceleration, then moves uniformly over a further distance 2l and finally comes to rest after moving a further distance 3l under uniform retardation. Assuming entire motion to be rectilinear motion the ratio of average speed over the journey to the maximum speed on its ways is
A $1 / 5$
B $2 / 5$
C $3 / 5$
D $4 / 5$
A particle starts from rest and traverses a distance 2x with uniform acceleration, then moves uniformly over a further distance 4x and finally comes to rest after moving a further distance 6x under uniform retardation. Assuming entire motion to be rectilinear motion, the ratio of average speed over the journey to the maximum speed on its way is
A $\frac{4}{5}$
B $\frac{3}{5}$
C $\frac{2}{5}$
D $\frac{1}{5}$
A particle starts from rest and travel a distance x with uniform acceleration, then moves uniformly a distance 2x and finally comes to rest after moving further 5x with uniform retardation. The ratio of maximum speed to average speed is
A $\frac{5}{2}$
B $\frac{5}{3}$
C $\frac{7}{4}$
D $\frac{7}{5}$