A body starts from rest and moves along a straight line path with uniform acceleration. The ratio of velocities at t = 1s and t = 2 s is ______.
2:1
1:2
1:√2
√2:1
The correct Answer is:B
To solve the problem, we need to find the ratio of velocities of a body moving with uniform acceleration at two different times: t=1 second and t=2 seconds.
1. Identify Initial Conditions:
- The body starts from rest, which means the initial velocity U=0.
- The body moves with uniform acceleration A.
2. Use the First Equation of Motion:
- The first equation of motion states that:
V=U+A⋅t
- Since U=0, this simplifies to:
V=A⋅t
3. Calculate Velocity at t=1 second:
- For t=1 second:
V1=A⋅1=A
4. Calculate Velocity at t=2 seconds:
- For t=2 seconds:
V2=A⋅2=2A
5. Find the Ratio of Velocities:
- Now, we need to find the ratio V1V2:
V1V2=A2A=12
6. Final Answer:
- The ratio of velocities at t=1 second and t=2 seconds is:
12
- The body starts from rest, which means the initial velocity U=0.
- The body moves with uniform acceleration A.
- The first equation of motion states that:
V=U+A⋅t
- Since U=0, this simplifies to:
V=A⋅t
- For t=1 second:
V1=A⋅1=A
- For t=2 seconds:
V2=A⋅2=2A
- Now, we need to find the ratio V1V2:
V1V2=A2A=12
- The ratio of velocities at t=1 second and t=2 seconds is:
12
Similar Questions
A body starts form rest and moves along a straight line path with uniform acceleration. The atio of velocities at 1= s and t= 2s is __________
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph
A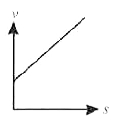 B
B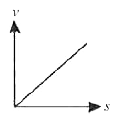 C
C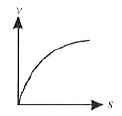 D
D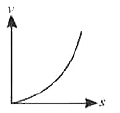
- Question 2 - Select One
A body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph
A√α2+β2B3t√α2+β2C3t2√α2β2Dt2√α2+β2 - Question 3 - Select One
A body start from rest and moves in a straight line with uniform acceleration F , the distances covered by in it second , fourth and eights seconds are
Ain arthmetic progressionBin geometrical progressionCin the ratio 1:3:7Din the ratio 3:7:15
A particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
 View Solution
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 View Solution
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 View Solution
View SolutionA body starting from rest moves along a string line with a constant acceleration The variation of speed (v) with distance (s) is repressed by the graph
View SolutionA body starting from the the rest moves along a straight line with constant acceleration. Which one of the following graphs represents the variation of speed(v) and distance(s)?
View Solution

