A rocket is launched from the suface of the earth vertically upward from rest. It moves under acceleration 8m/s2. After 15 s the fuel is finished, the rocket moves under gravity and ultimately strickes the ground. Assuming upward direction position and launching point as the origin, sketch the v-t, s-t and a-t graph.
Here the motion is in two parts: first acceleration and then motion under gravity.
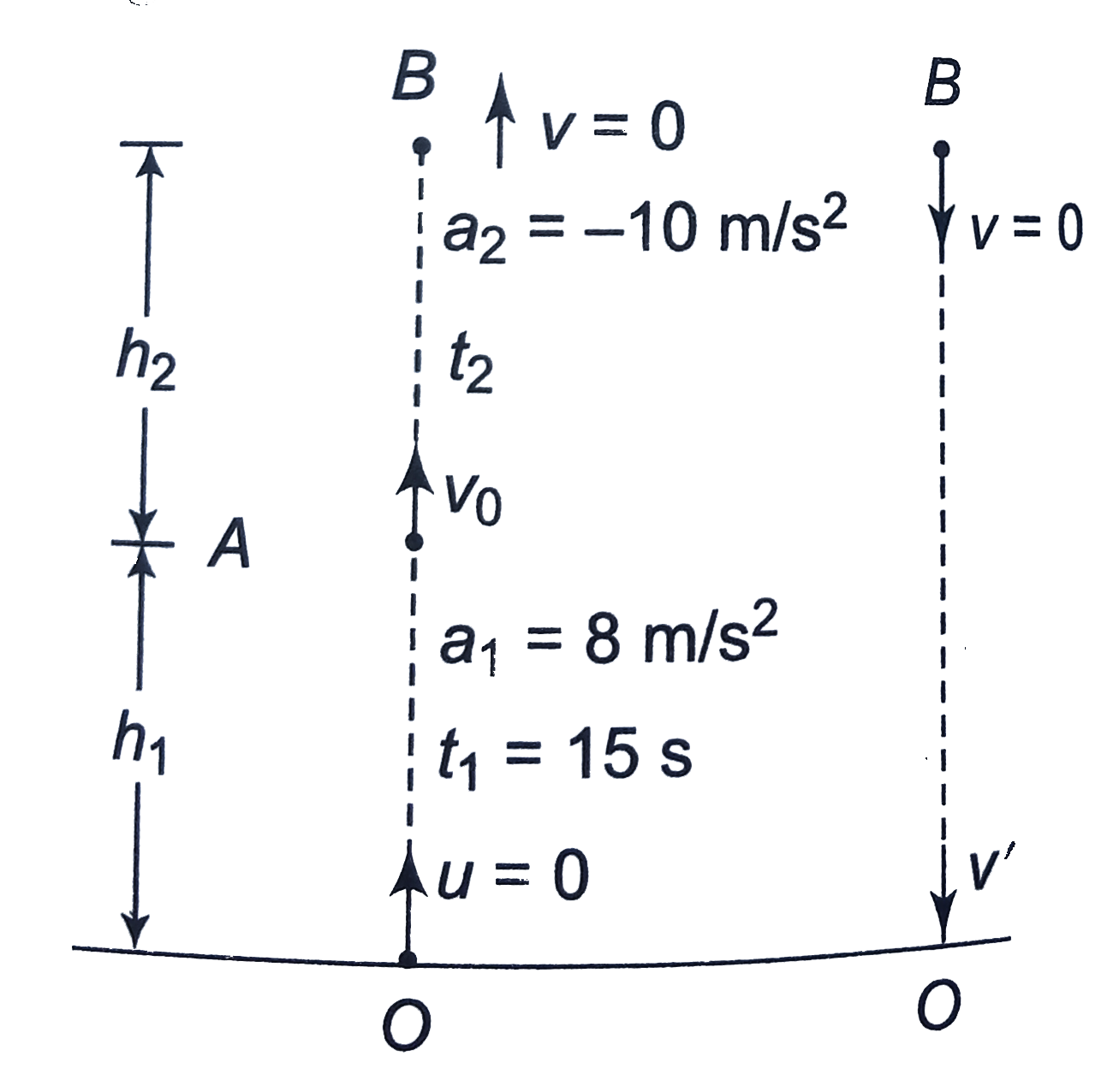
Acceleration motion
O to A: h1=0+12a1t21=12×8×(15)2=900m
A to O through B
A: Origin
Displacement=−900m
S=ut−12at2
−900=v0t2−12a2t22=120t2−5t22
t22−24t2−180=0
t2=24±√(−24)2−4(1)(−180)2
=24±362
t2=30s, the rocket will strike the ground after 30 s (after the fuel is finished)
v′=u−gt2
=v0−gt2
=120−10×30=−180m/s
The velocity of the rocket will be zero after time t3. So,
0=120−10t3⇒t3=12s
To obtain the maximum height attained by the rocket above A, we have
0=(v0)2−2×10×h2⇒h2=720m at time
t′=12s
Total time of journey =15+30=45s
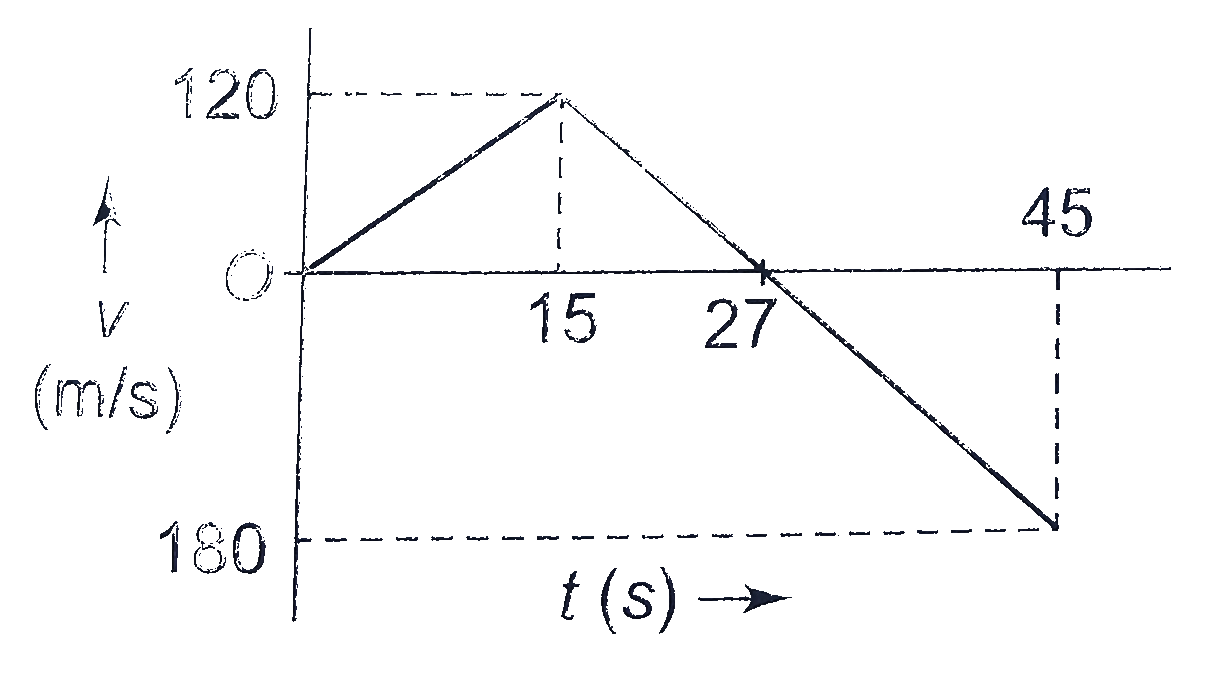
v-t graph
t=0,v=0
t=15s,v=120m/s
t=27s,v=0
t=45s,v=−180m/s
t=0 to t=15s, v=8t (straight line)
t=15 to t=45s
v=120−10(t−15) (straight line) [15s<=t<=45s]
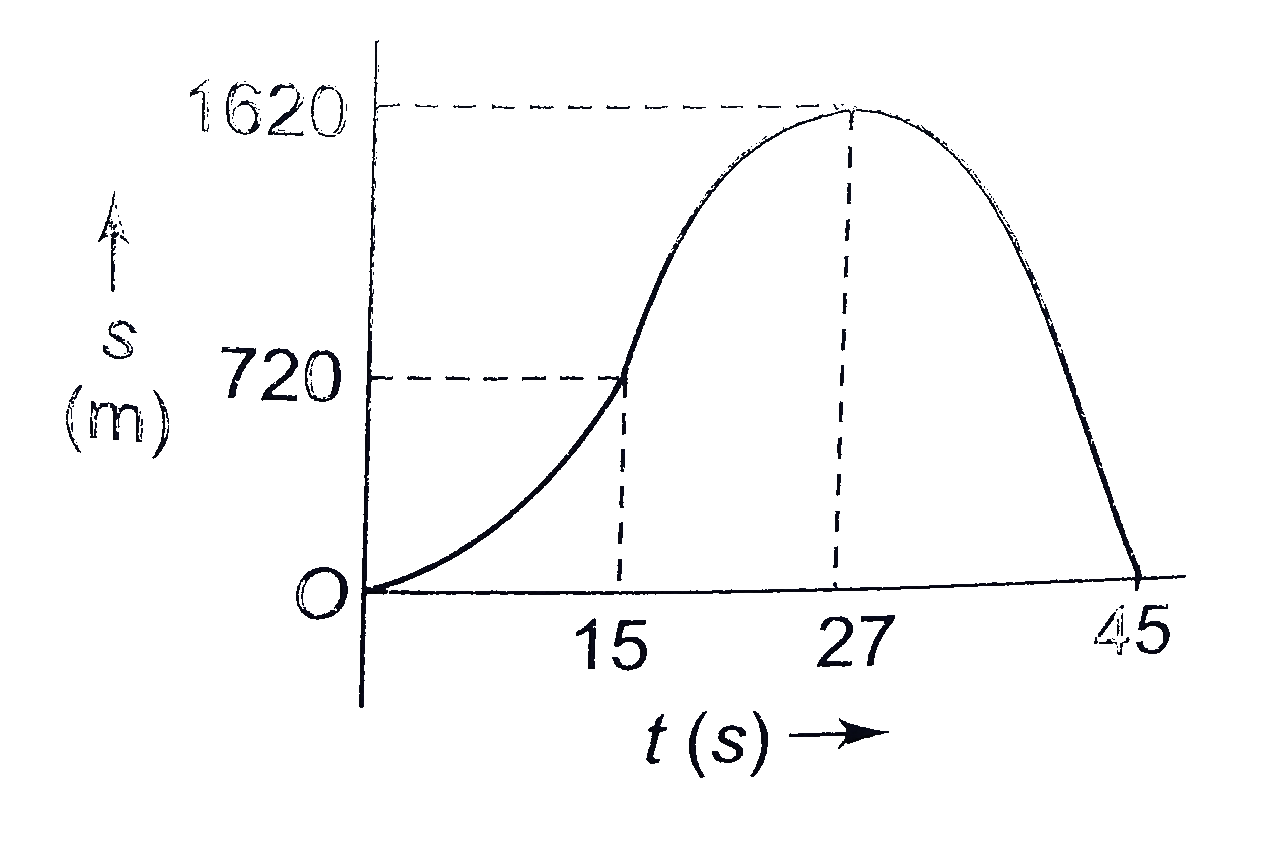
s-t graph
t=0,s=0
t=15s,s=900m
t=27s,s,s=900+720=1620m
t=45s,s=0
t=0 to t=15s, s=12a1t2⇒s=4t2
Shape: y=4x2 (parabola, open upward)
t=15→45s
s=900+v0(t−15)−12a2(t−15)2
=900+120(t−15)−5(t−15)2
Shape: y=900+120x−5x2 (parabola, open downward)
Topper's Solved these Questions
Similar Questions
A balloon carrying a stone rises from rest on the ground with a constant acceleration 10m/s2. After 5 s, the stone is released and ultimately it strikes the ground. Sketch a v-t graph for the stone and the maximum height attained by it.
View SolutionA rocket is fired vertically from the ground. It moves upwards with a constant acceleration 10m/s2 after 30 sec the fuel is finished. After what time from the instant of firing the rocket will attain the maximum height? g=10m/s2:-
View Solution
Knowledge Check
A rocket is fired vertically upwards and moves with net acceleration of 10m/s2. After 1 min the fuel is exhausted. The time taken by it to reach the highest point after the fuel is exhausted will be:
A10 secB20 secC30 secD60 secA rocket is fired upward from the earth's surface such that it creates an acceleration of 20m/s2. If after 5 s its engine is switched off, the maximum height of the rochet from the earth's surface would be
A250 mB500 mC750 mD1000 mThe maximum height is reached is 5s by a stone thrown vertically upwards and moving under the equation 10s=10ut−49t2, where s is in metre and t is in second. The value of u is
A4.9ms−1B49ms−1C98ms−1DNone of these
A rocket is fired vertically from the ground. It moves upwards with a constant acceleration 10m/s2 after 30 sec the fuel is finished. After what time from the instant of firing the rocket will attain the maximum height? g=10m/s2:-
View SolutionA prototype of a rocket is fired from the ground. The rocket rises vertically up with a uniform acceleration of 54m/s2. 8 second after the start a small nut gets detached from the rocket. Assume that the rocket keeps rising with the constant acceleration.
(a) What is the height of the rocket at the instant the nut lands on the ground
(b) Plot the velocity – time graph for the motion of the nut after it separates from the rocket till it hits the ground. Plot the same velocity– time graph in the reference frame of the rocket. Take vertically upward direction as positive and g=10m/s2
View SolutionA particle is dropped from the top of a tower of height 80 m. Assuming the dropping point as the origin and the downward direction position, sketch v-t, s-t and a-t graph. (g=10m/s2)
View SolutionA rocket is fired vertically upward from the ground with a resultant vertical acceration of 5m/s2. The fuel is finished in 100s and it continues to move up. After how much time from then will the maximum height be reached and what is the maximum height?
View SolutionFrom the top of a toward of height 60m, a ball is thrown vertically upward with speed 20m/s. After some time, the ball strikes the ground. Sketch the v-t and s-t graph.
View Solution
