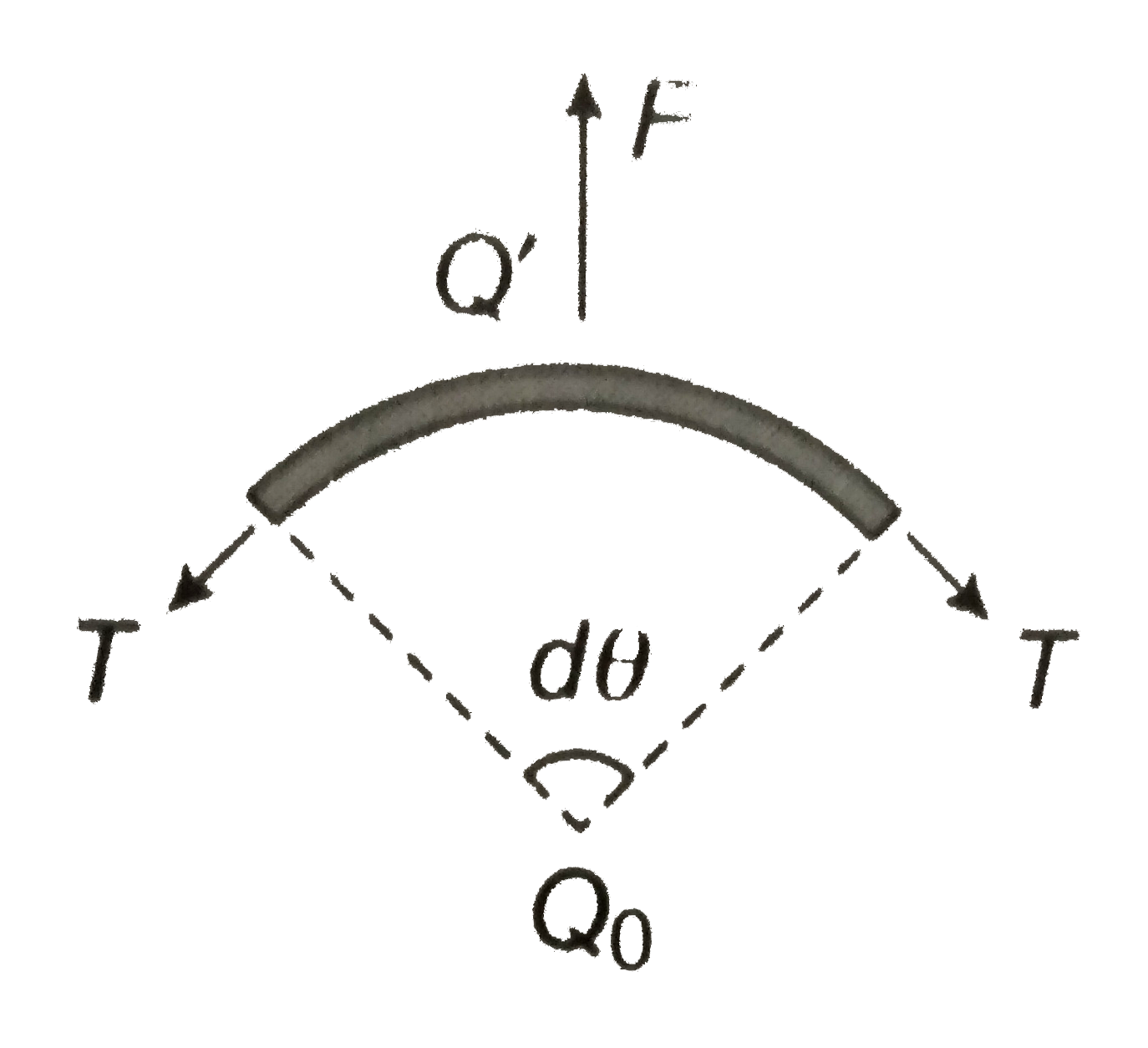
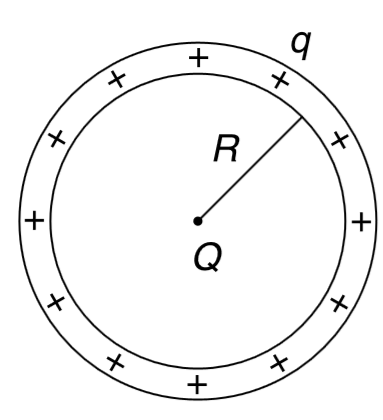
A ring of radius $R$ is having charge $Q$ uniformly distributed. A point charge $Q_{0}$ is placed at the centre of the ring. Find tension developed in the ring. If radius of cross - section of the ring is $a$ and Young's modulus of wire is $Y$ , find increase in the radius of ring.

Text Solution

Verified by Experts

To find tension//compression in the ring, find the force on small length of angle $d θ$ and remove $d θ$ from the expression (refer to Circular Motion , Example 33 , page 351 Vol. 1).
Charge on small length of angle $d θ$
$Q' = \frac{Q}{2 π R} d l = \frac{Q}{2 π R} R d θ = \frac{Q d θ}{2 π}$
Electric force on $Q'$ ,
$F = \frac{1}{4 π \in_{0}} \frac{Q' Q_{0}}{R^{2}} = \frac{1}{4 π \in_{0}} . \frac{Q Q_{0}}{2 π R^{2}} d θ$
Tension in the string
$T = \frac{Q Q_{0}}{8 π^{2} \in_{0} R^{2}}$
Let increase in the radius of ring is $Δ R$ .
Longitudinal strain
$\in = \frac{2 π (R + Δ R) - 2 π R}{2 π R} = \frac{Δ R}{R}$
Longitudinal stress
$σ = \frac{T}{A} = \frac{T}{π d^{2}}$
where $a$ : radius of cross - section of ring.
$Y = \frac{σ}{\in} = \frac{T / π a^{2}}{Δ R / R}$
$Δ R = \frac{T R}{π a^{2} Y} = \frac{Q Q_{0}}{8 π^{2} \in_{0} R^{2}} . \frac{R}{π a^{2} Y}$
$= \frac{Q Q_{0}}{8 π^{3} \in_{0} R Y a^{2}}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

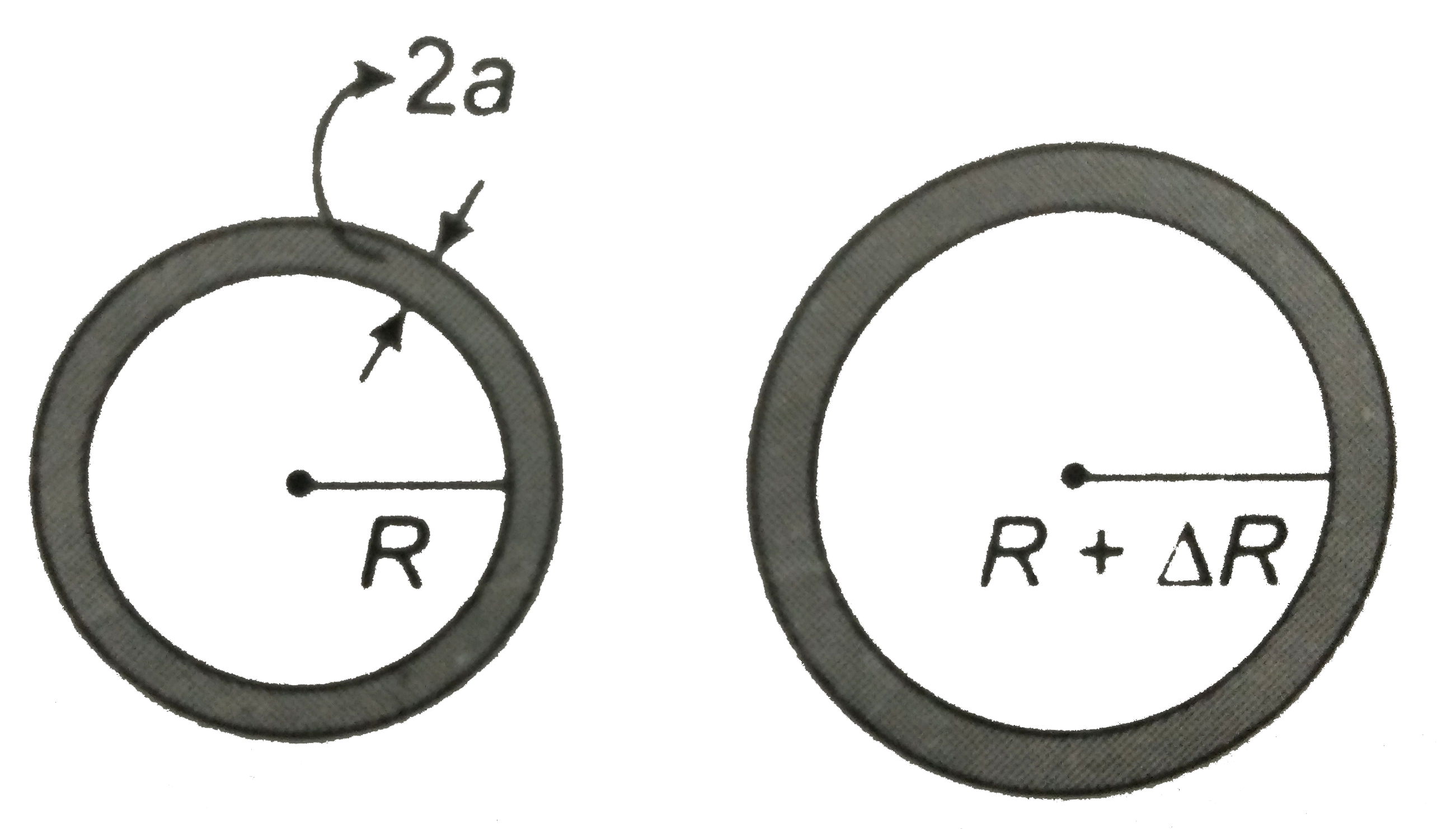
Topper's Solved these Questions

Similar Questions

Knowledge Check

Charges $q$ is uniformly distributed over a thin half ring of radius $R$ . The electric field at the centre of the ring is
A $\frac{q}{2 π^{2} ε_{0} R^{2}}$
B $\frac{q}{4 π^{2} ε_{0} R^{2}}$
C $\frac{q}{4 π ε_{0} R^{2}}$
D $\frac{q}{2 π ε_{0} R^{2}}$

CP SINGH-ELECTROSTATICS-Exercises

Home
Ask Doubt
Profile