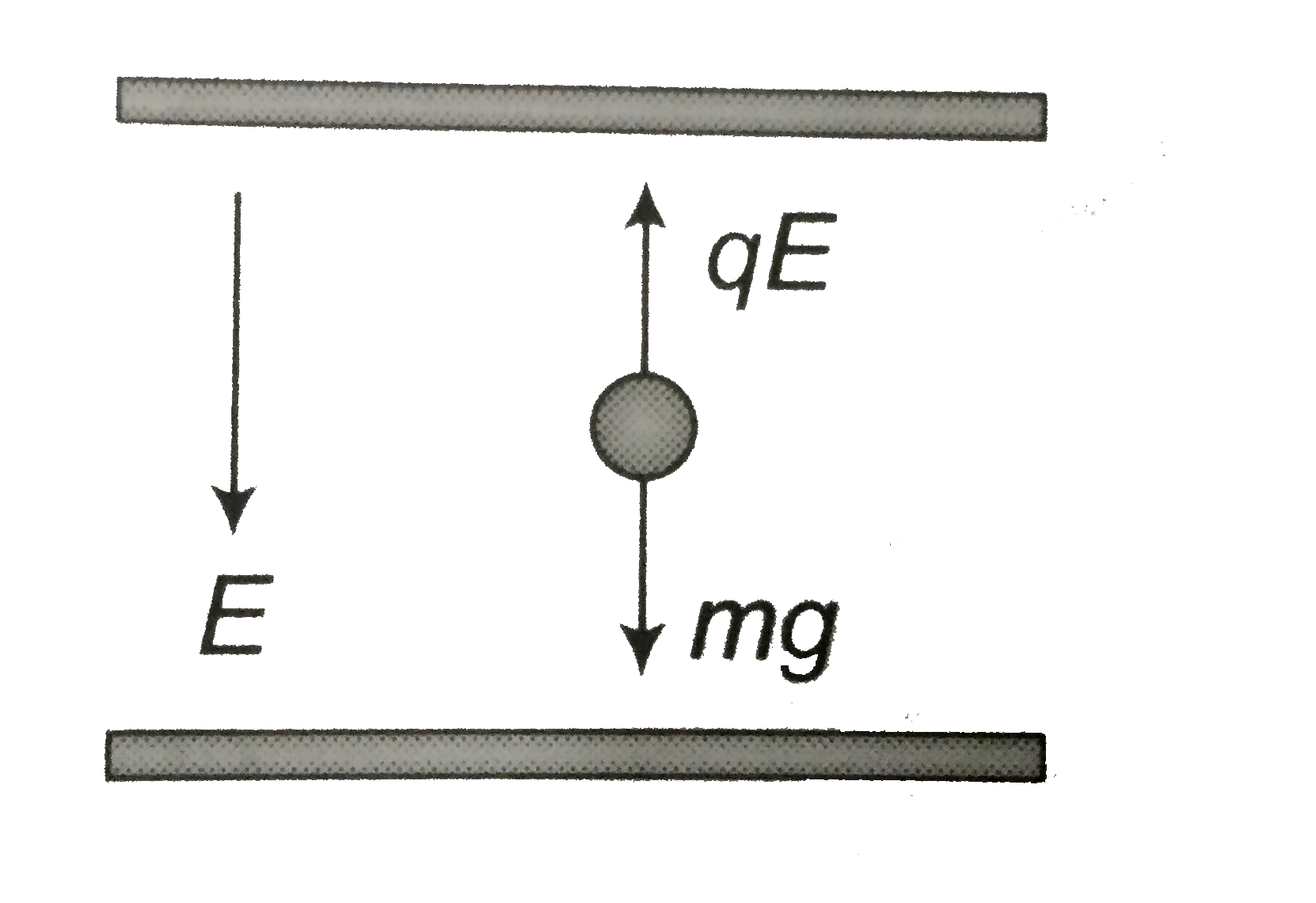
Between two horizontal parallel plates, uniform electric field E directed vertically downward. A charged particle (q,m) remains in equilibrium in vaccum between the plates. Find shortage/excess of electrons in the charged particle .
Since particle is in equilibrium i.e. net force on it is zero. The weight of particle is balanced by electric force. Since electric force is in upward direction , hence charge q is negative i.e. excess of electrons
qE=mg⇒q=mgE
ne=mgE⇒n=mgeE
where n: number of electrons in excess.
Topper's Solved these Questions
Similar Questions
A charged ball with mass m and charge q is dropped from a height h over a non-conducting smooth horizontal plane. There exists a uniform electric field E0 in vertically downward direction and the coefficient of restitution between the ball and the plane is e. Find the maximum height attained by the ball after nth collision.
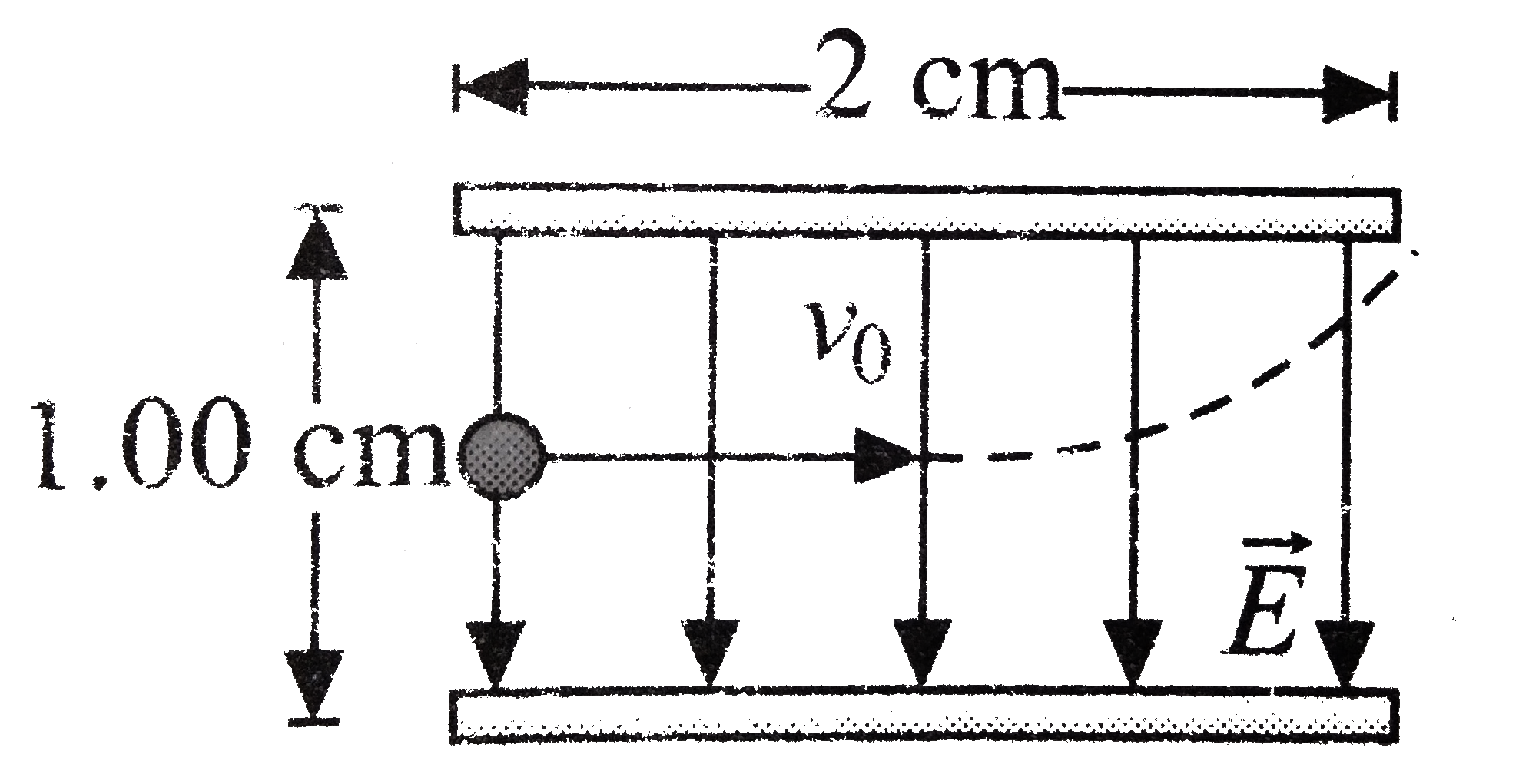
View SolutionAn electron (e,m) is projected into a uniform electric field E vertically downward between parallel plates at separation d, with velocity v0. The electron enters the electric field at a point midway between the plates. Find
(a) the magnitude of electric field if electron emerges from the electric field just at the edge of upper plate.
(b) the direction of the velocity of electron as it emerges from the electric field.
(c ) the equation of trajectory followed by electron.
The length of plates is L and consider only electric force.
View Solution
Knowledge Check
A uniform electric field →E exists between the plates of a charged condenser. A charged particle enters the space between the plates and perpendiculars to →E. The path of the particle between the plates is a
AStraight lineBhyperbolaCparabolaDcircleAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.
The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).A1.6×10−8mB3.25×10−8mC5.25×10−6mD2.73×10−6mA simple pendulum having caharge q1 mass ma and effective length 1, is suspended from a rigid support between the plates of charged horizontal capacitor. Electric field in the capacitor is perpendicular to the plates and directed vertically downwards .
the angle α between the equilibrium position of the pendulum and the vertical is given by.Aα=sin−1[(qQE/m)sinθh+(qE/m)vodθ]Bα=cos−1[(qQE/m)sinθh+(qE/m)vodθ]Cα=tan−1[(qQE/m)sinθh+(qE/m)vodθ]Dα=cos−1[(qQE/m)sinθh+(qE/m)vodθ]
Two parallel conducting plates , a distance d apart, are held horizontally one above the other in air . Between parallel plates , electric field E is uniform and directed vertically downwards . A spherical ball of radius r, made of a material of density σ falls with constant velocity v. the coefficient of viscosity of air is η and density of air is negligible in comparision of σ. Find electric charge on ball assuming it to be positive.
View SolutionA charges particles particle is kept in equilibrium in the electric field between the plates of millikan oil drop experiment. If the direction of the electric field between the plates is reversed, then calculate acceleration of the charged particle.
View SolutionHow will the electric field between the plates in parallel plate capacitor change, if the charge on the plates is doubled?
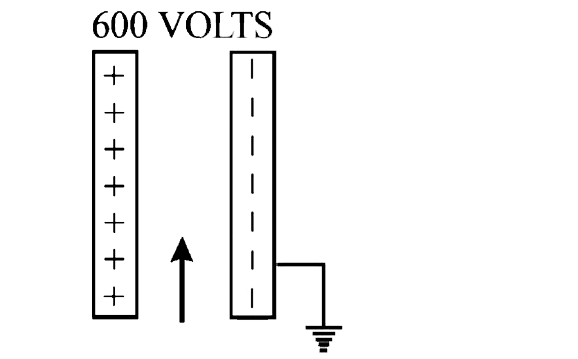
View SolutionA potential difference of 600vo<s is applied across the plates of a parallel plate consenser . The separation between the plates is 3mm. An electron projected vertically, parallel to the plates , with a velocity of 2×106m/sec moves underflected between the plates. Find the magnitude and direction of the magnetic field in the region between the condenser plates. ( Neglect the edge effects). ( Charge of the electron = -1.6xx10^(-19) coulomb)
View SolutionA parallel plate air condenser is charged and then disconnected from the charging battery. Now the space between the plates is filled with a dielectric then, it electric field strength between the plates
View Solution
