A block of mass m having charge q is attached to a spring of spring constant k. This arrangement is placed in uniform electric field E on smooth horizontal surface as shown in the figure. Initially spring in unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.
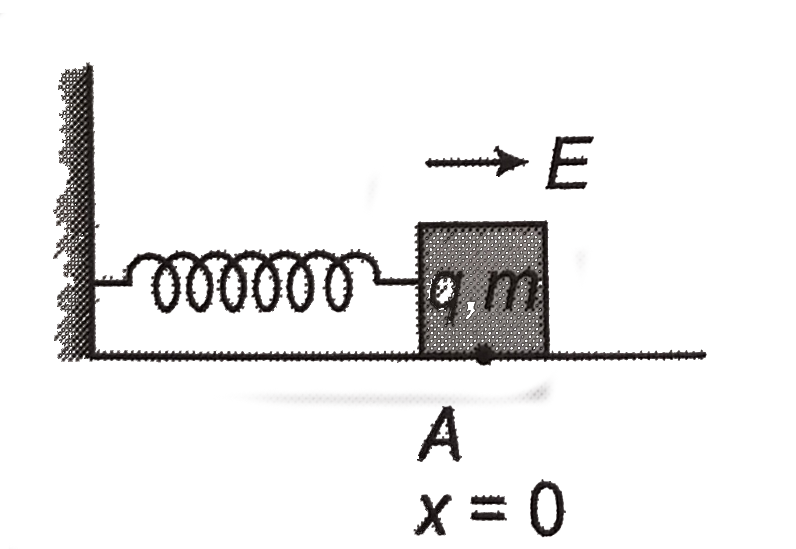
Due to electric force qE acting on the block , spring extends. Let at some instant extension of spring be x.
Net force on block , Fnet=qE−kx
In equilibrium , Fnet=qE−kx=0
x=x0=qEk
In equilibrium , extension of spring x0=qEk
Maximum extension =2x0=2qEk
OR
where x' : maximum extension .
12kx'2=qEx'⇒x'=2qEk
In fact , the block is executing S.H.M. of time period
T=2π√mk , amplitude of oscillation =qEk

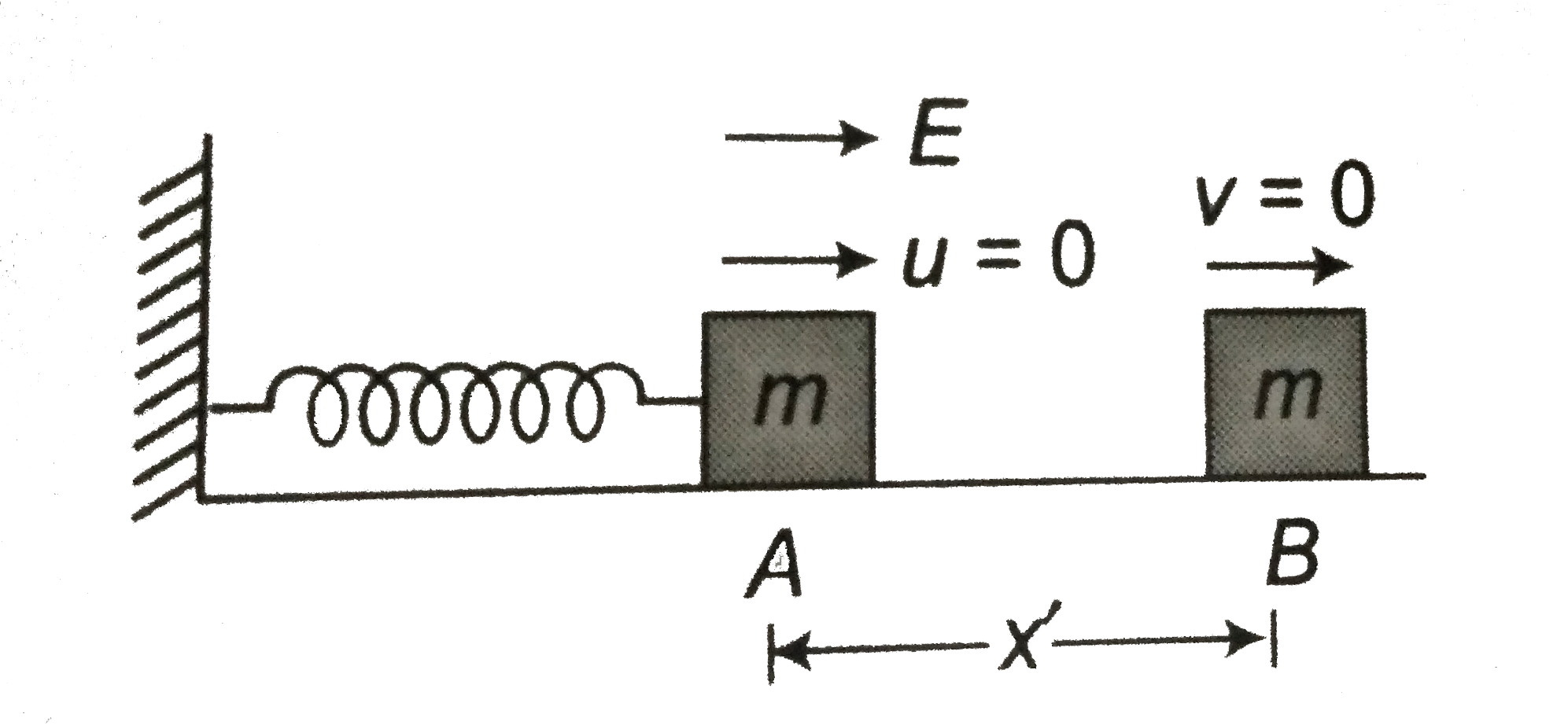
Topper's Solved these Questions
Similar Questions
Initially block shown is at rest and the spring is unstretched, when a constant force F begins to act on it neglect friction. Find
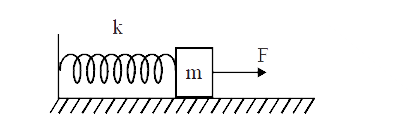
maximum extension in the springView SolutionTwo block-spring mass system are moving on smooth horizontal surface as shown in the figure as t=0. find out the minimum time t when the spring is maximum elongated l0 is the natural length of spring.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Initially spring is in natural length and both blocks are in rest condition. Then deter mine
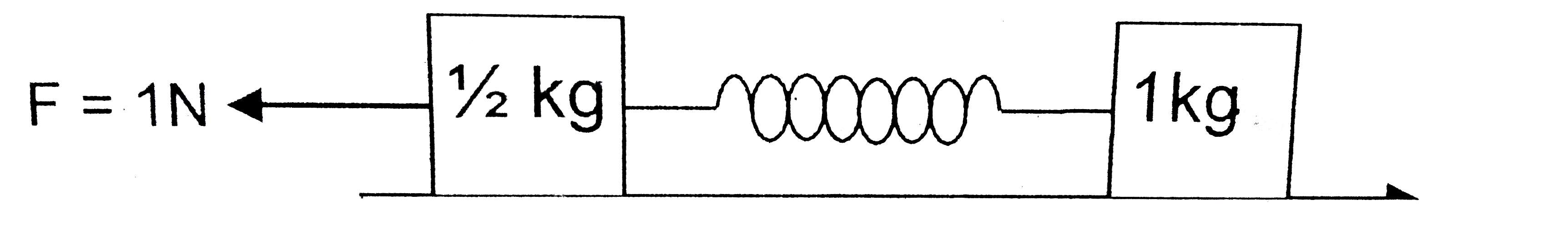
maximum extension in spring . K = 20 N/MA203cmB103cmC403cmD193cm - Question 2 - Select One
An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
A(a) 4MgkB(b) 2MgkC(c) MgkD(d) Mg2k - Question 3 - Select One
A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of these
A block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring
 View Solution
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.
 View Solution
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.
 View Solution
View Solution
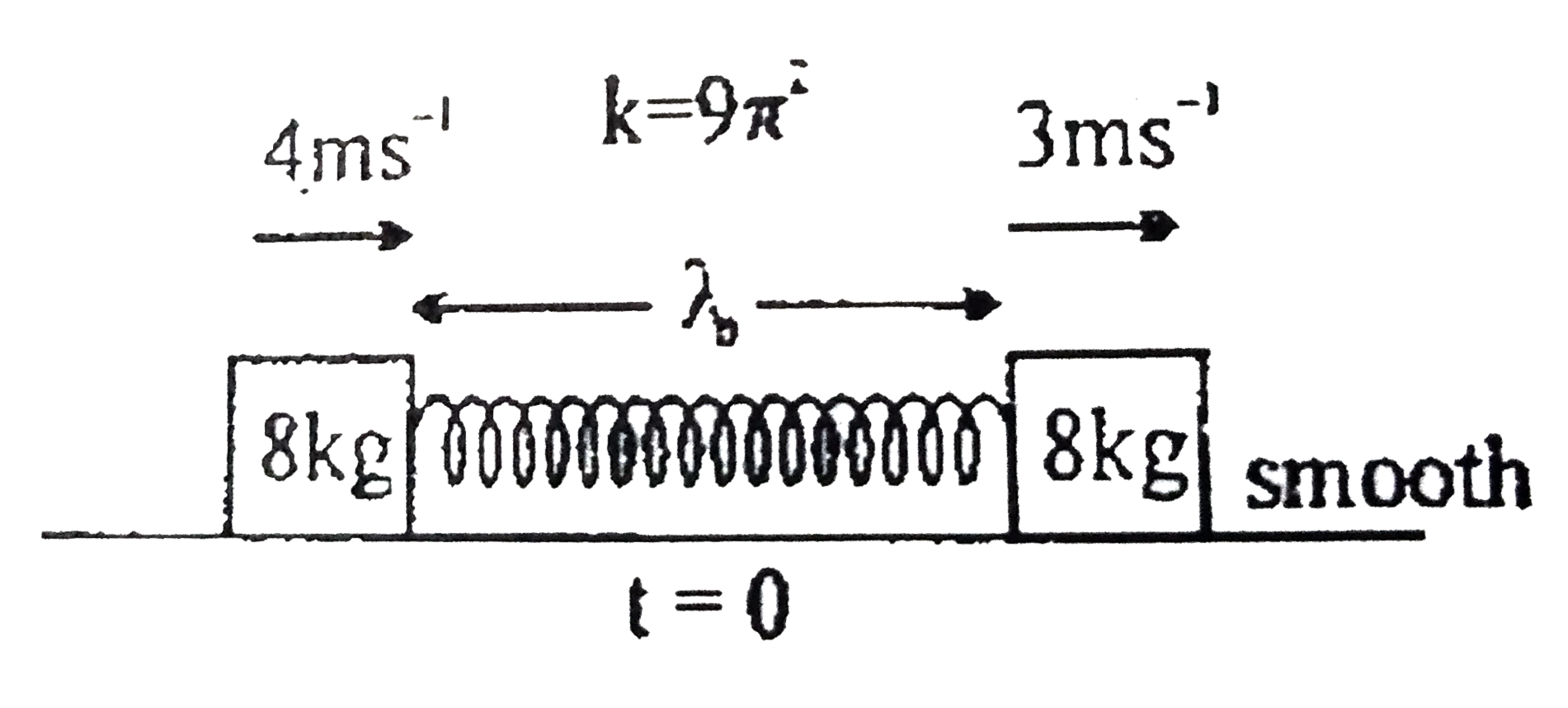
Consider the situation as shown. Initially the spring is unstretched when the block of mass m is released from rest assuming the pulley frictionless and light the spring and string massless. Find the extension of sprinig when the block is in equilibrium also find the maximum extension of the spring.View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
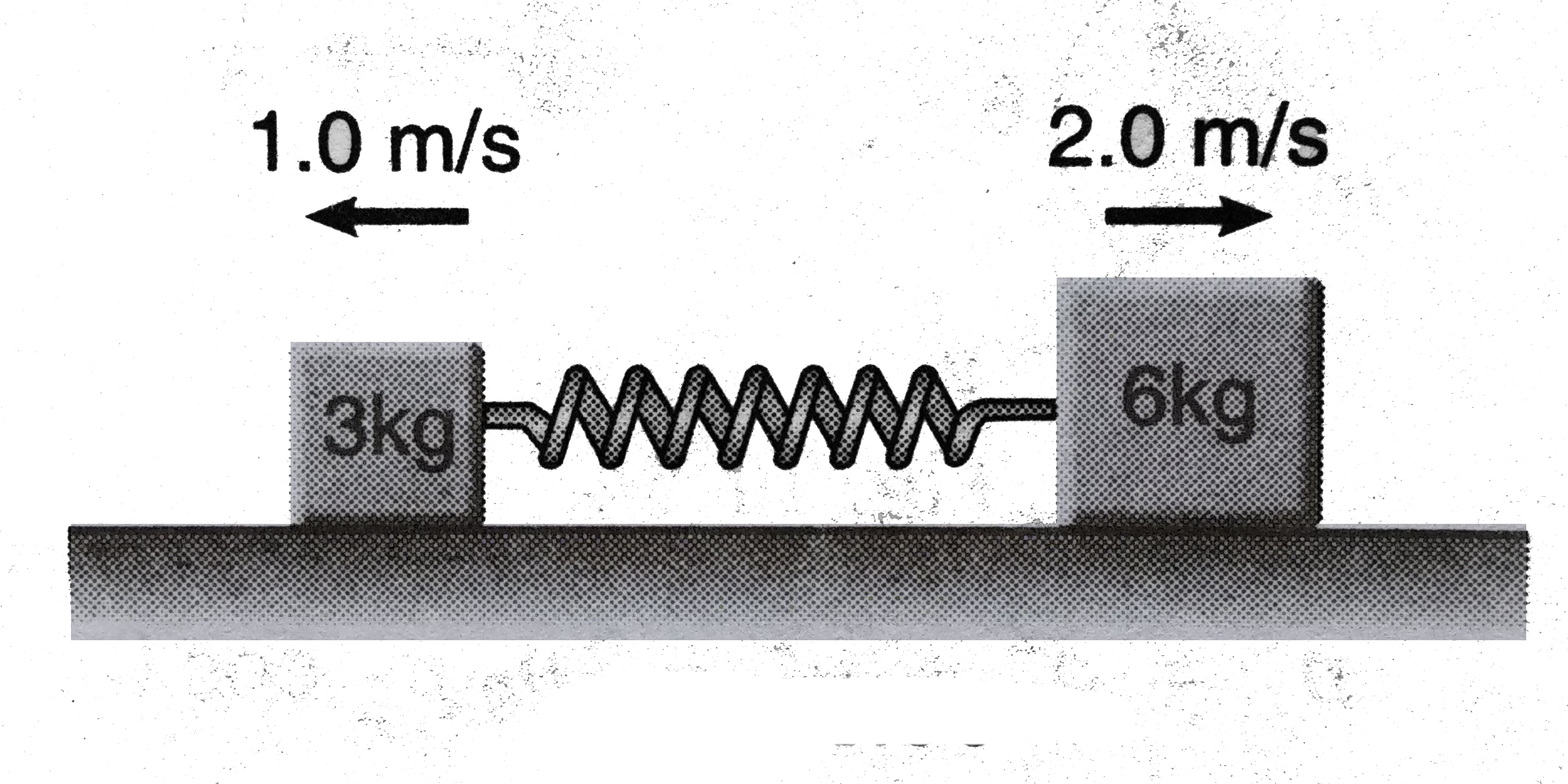 View Solution
View Solution

