
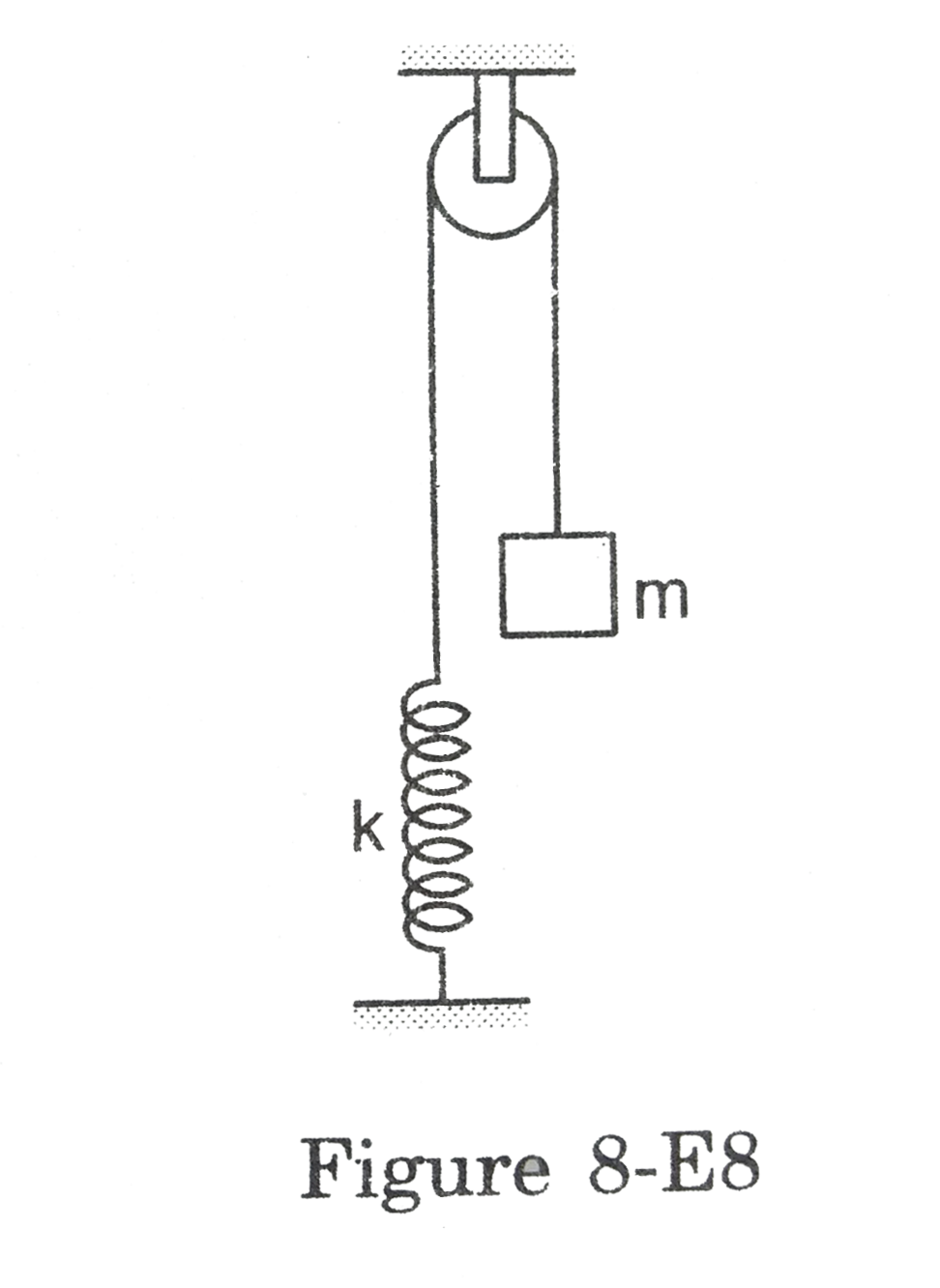
Consider the situation as shown. Initially the spring is unstretched when the block of mass m is released from rest assuming the pulley frictionless and light the spring and string massless. Find the extension of sprinig when the block is in equilibrium also find the maximum extension of the spring.

when the block is in equilibrium thenet force on it is zero.
In equilibrium mg=kx0
x0=mgk
Where x0 is an extension of spring when the block is in equilibrium.
Maximum extension of spring let at some isntant the extension of spring be x.
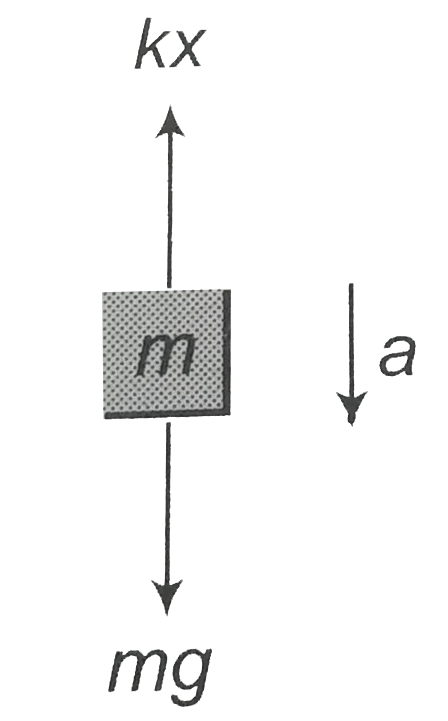 ltbgt mg−kx=ma
ltbgt mg−kx=ma
a=g−kmx ltbgt vdvdx=g−kmx
∫v0∫vdv=x∫0(g−kmx)dx
∣∣∣v22∣∣∣v0=∣∣∣gx−kx22m∣∣∣x0
v22=gx−kx22m
v=(2gx−kx2m)12
where v is the velocity of the block as the function of eextension of spring
the block will stop when
v=0
(2gx−kx2m)1/2=0
x=xm=2mgk
where xm is the maximum extension in the spring.
Topper's Solved these Questions
Similar Questions
Consider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the puley, find the maximum eleongation of the spring.
 View Solution
View SolutionConsider the situations shown in fig (a) and (b) initially the spring is unstretched when the mass m is released from rest. Assuming no friction in the pulley find (a) the maximum stretch in the spring (b) stretch in the spring when the system is in equilibium.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Find the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 AmgBmg/2C3mg/2D2 mg
AmgBmg/2C3mg/2D2 mg - Question 2 - Select One
A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k - Question 3 - Select One
A block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
 A√m2KV0B√mKv0C√2mKv0D2√mKv0
A√m2KV0B√mKv0C√2mKv0D2√mKv0
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
 View Solution
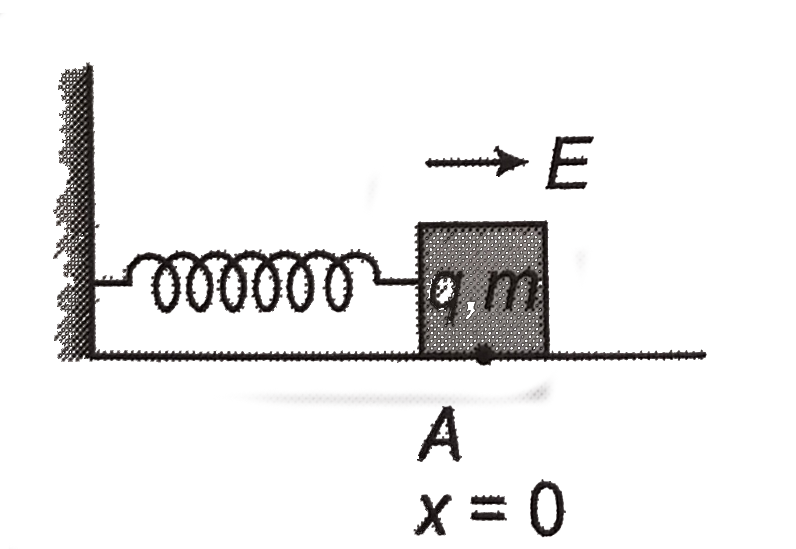
View SolutionA block of mass m having charge q is attached to a spring of spring constant k. This arrangement is placed in uniform electric field E on smooth horizontal surface as shown in the figure. Initially spring in unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.
 View Solution
View SolutionInitially block shown is at rest and the spring is unstretched, when a constant force F begins to act on it neglect friction. Find
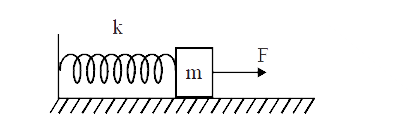
maximum extension in the springView SolutionThe system shown in th fig is released from rest. (Neglecting friction and mass of the pulley, string and spring). The spring can be elongated:
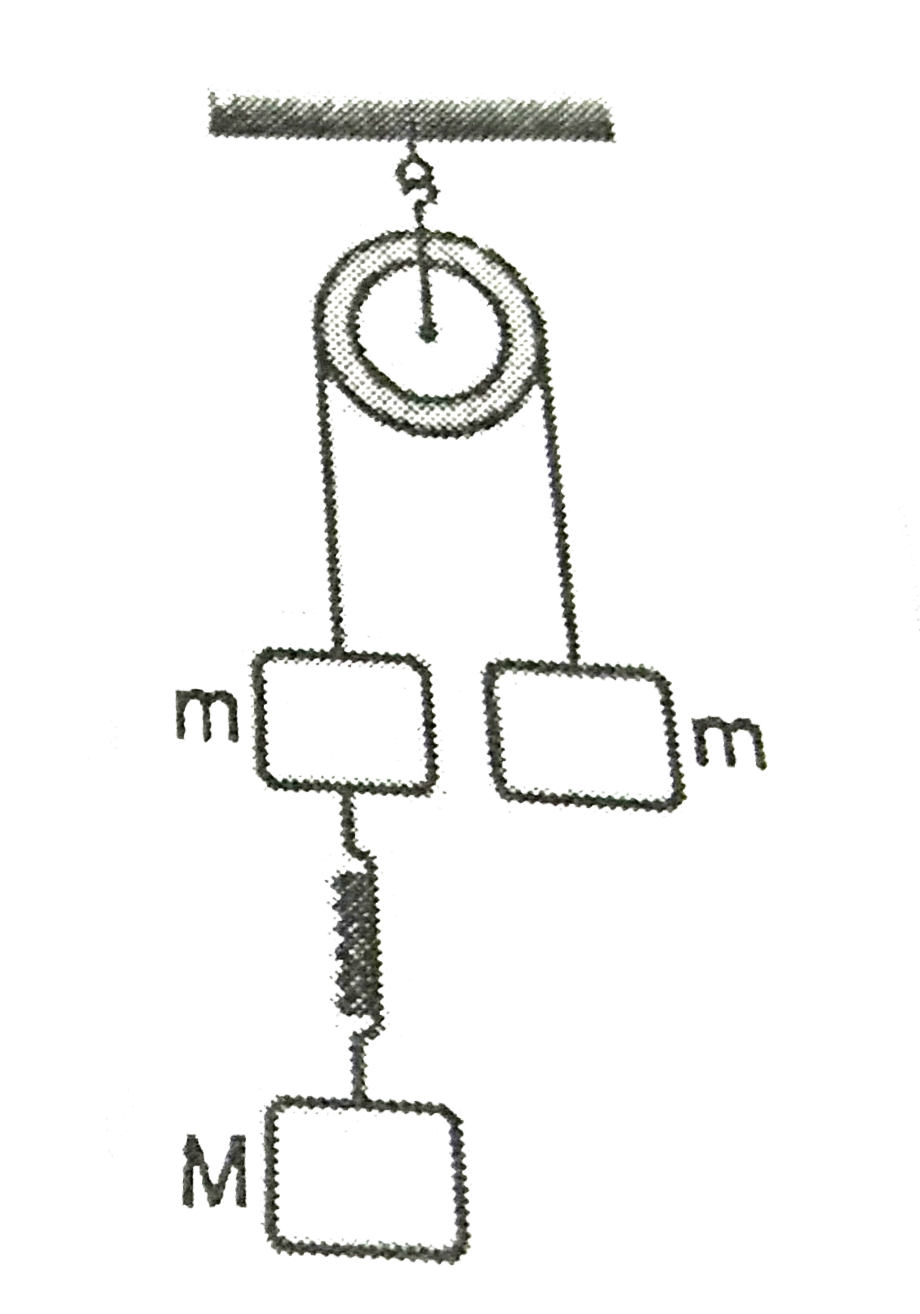 View Solution
View Solution

