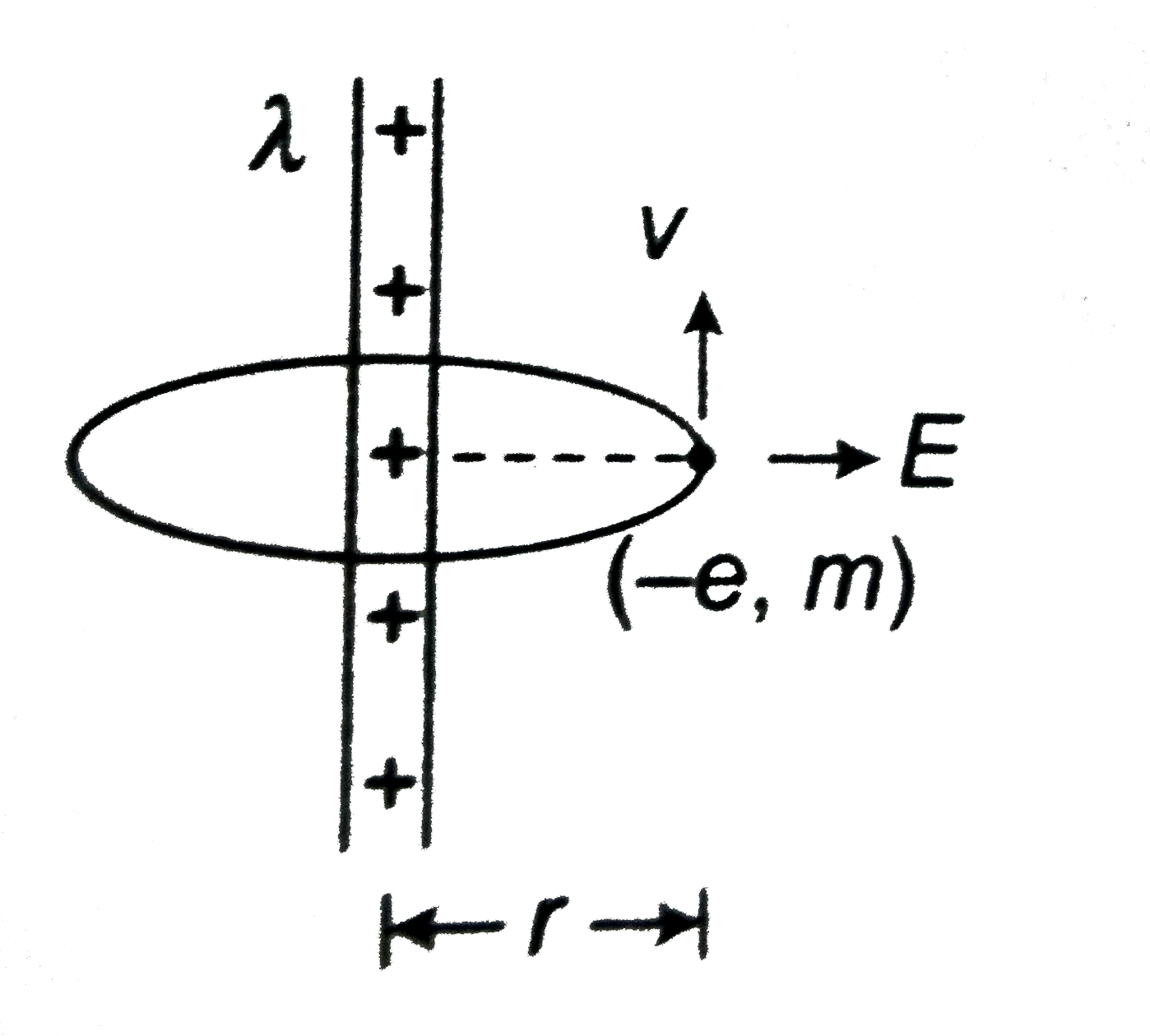
A long cylindrical wire carries a positive charge of linear density la

An electron is revolving around a proton in a circular path of diameter 0.1 fm. It produces a magnetic field 14 tesla at a proton. Then the angular speed of the electron is
A $8.8 \times 10^{16} r a d s^{- 1}$
B $4.4 \times 10^{16} r a d s^{- 1}$
C $1.1 \times 10^{16} r a d s^{- 1}$
D $1.1 \times 10^{16} r a d s^{- 1}$
A long straight wire carries a charge with linear density $λ$ . A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
A $\sqrt{\frac{q λ ln r}{π m \in_{0}}}$
B $\sqrt{\frac{q λ ln 2}{π m \in_{0}}}$
C $\sqrt{\frac{q λ ln 2}{2 π m \in_{0}}}$
D $\sqrt{\frac{q λ ln 2}{π m \in_{0}}}$
An electron moves along a circular path of radius 10 cm. If the centripetal acceleration is $4 \times 10^{11} m / s^{2}$ , then its linear speed is
A $0.5 \times 10^{5} m / s$
B $10^{5} m / s$
C $2 \times 10^{5} m / s$
D $3 \times 10^{5} m / s$

A long cylindrical wire carries a positive charge of linear density $λ$ . An electron $(- e, m)$ revolves around it in a circular path under the influence of the attractive electrostatic force. Find the speed of the electron.