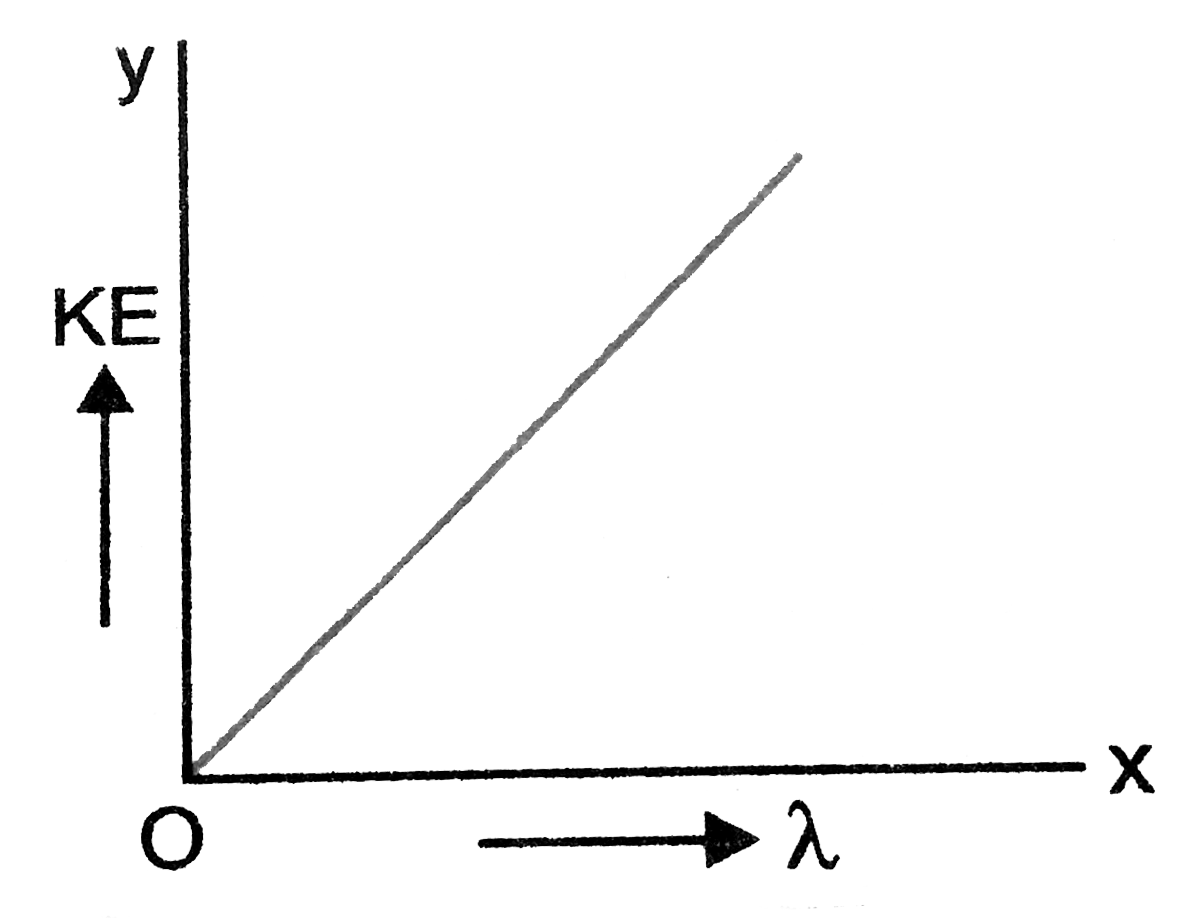
An indinitely long positively charged wire has a linear charge density λcm−1. An electron is revolving around the wire as its center with a constant velocity in a circular plane perpendicular to the wire. Deduce the expression for KE of electron. Plot a graph of K.E as a function of charge density λ.
The electostatic force exerted by the infinitely long line charge provides the necessary centripetal force to the revolving electron.
∴eE=mv2r,butE=λ2π∈0r
eλ2π∈0r=mv2rorv2=eλ2π∈0m
KE=12mv2=12m(eλ2π∈0m)=eλ4π∈0
As KE ∝λ, therefore, graph of KE as a function of charge density will be a straight line as shown in Fig.
Similar Questions
A long cylindrical wire carries a positive charge of linear density λ. An electron (−e,m) revolves around it in a circular path under the influence of the attractive electrostatic force. Find the speed of the electron.
View SolutionA semi-infinite insulating rod has linear charge density λ. The electric field atthe pointPshown in figure-1.418 is:

View Solution
Knowledge Check
An infinitely long thin straight wire has uniform linear charge density of 1/3coulm−1 .Then the magnitude of the electric intensity at a point 18cm away is
A0.33×1011N/CB3×1011NC−1C0.66×1011NC−1D1.32×1011NC−1An infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
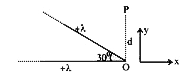 Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]Find ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
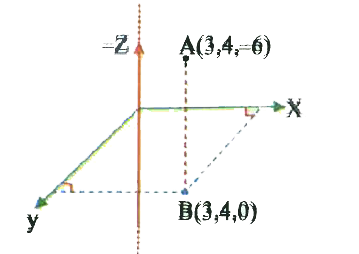 A1:2B1:6C6:1D1:1
A1:2B1:6C6:1D1:1
There is one long line charge with linear charge density λ. One electron is moving in a circular path around this line charge. Plane of the circle is perpendicular to line charge and line charge passes through centre of circle. Prove that kinetic energy of electron is independent to the radius of a circle.
View SolutionConsider a very long plastic wire with charge density λ .Flux passing through a circle of radius R having centre at one of ends of wire is
View SolutionA long cylindrical wire carries a positive charge of linear density 2.0 xxx 10^(-8) C m^(-1). An electron revolves around it in a circular path under the influence of the attactive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
View SolutionIf linear charge density of a wire as shown in the figure is λ

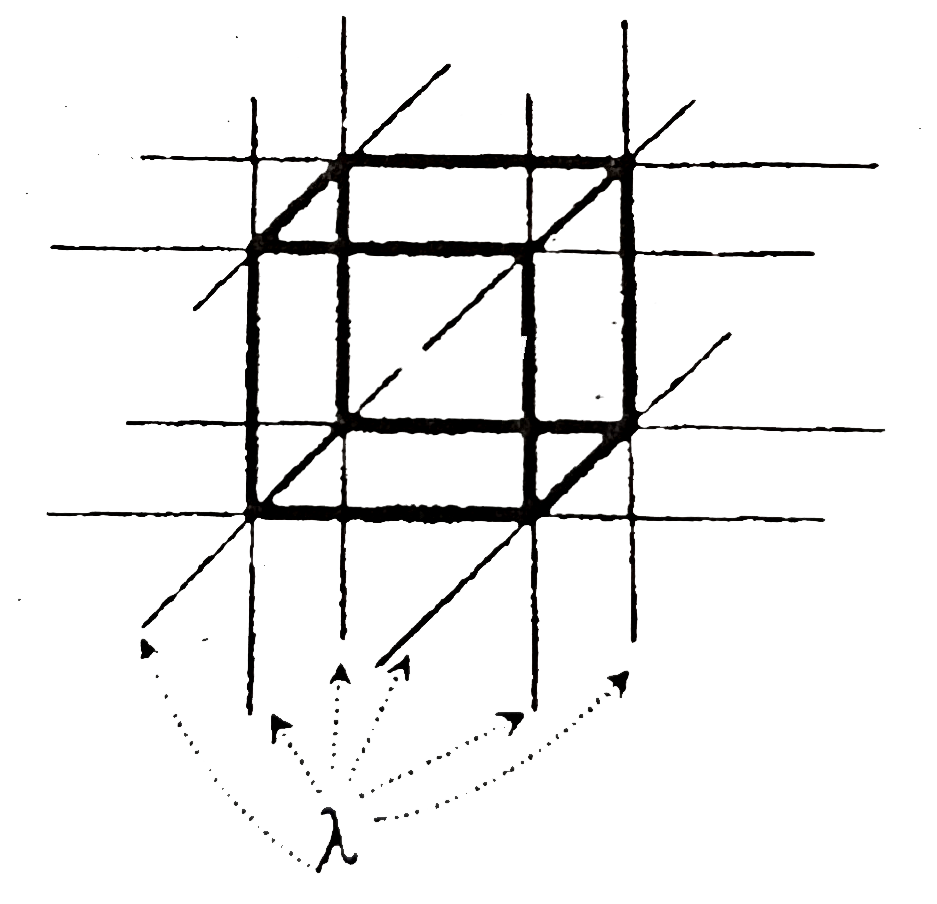
View SolutionTwelve infinite long wire of uniform linear charge density (λ) are passing along the twelve edges of a cube. Find electric flux through any face of cube. ,
View Solution
