There is infinitely long straight thread carrying a charge with linear density λ.Calculate the potential difference A and B.

The electric field at perpendicular x from wire
→E=λ2π∈0xˆi,dxˆi+dyˆj+dzˆk
→E.d→r=λ2π∈0xdx
VA−VB=−∫dηd→E.d→r=−∫dηd|logex|dηd
=−λ2π∈0loge(1η)
=λ2π∈0loge(η)
Topper's Solved these Questions
Similar Questions
There is an infinitely long straight thread carrying a charge with linear density λ=0.40μC/m. Calculate the potentail difference between points I and 2 is removed η=2.0 times farhter from the thread than point 1.
View SolutionAn infinitely long straight conductor carrying a charge with a linear density +T and a point charge −Q are at a certain distance from each other. In which of the three regions (I, II or III) are there points that (a) lie on the line passing through tho point charge perpendicular to the conductor. and (b) at which ..th~ field strength is zero 1)
View Solution
Knowledge Check
An infinite thread of charge density λ lies along z-axis. The potential difference between points A(4,3,4) and (3,4,0) is
 Aλ2π∈0In(√415)Bλ2π∈0In(5)CzeroDλ2π∈0
Aλ2π∈0In(√415)Bλ2π∈0In(5)CzeroDλ2π∈0A long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
A√qλlnrπm∈0B√qλln2πm∈0C√qλln22πm∈0D√qλln2πm∈0The magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
A|B|=(μ04π)2irB|B|=(μ04π)r2iC|B|=(4πμ0)2irD|B|=(4πμ0)r2i
(a) There is an infinitely long thread uniformly charged with linear charge density λC/m. Using Gauss’ law, calculate the electric field (E0) at a distance x from the thread. (b) Now consider a semi-infinite uniformly charged thread (linear charge density =λ) as shown in figure. Find the y component of electric field at point P in terms of E0. Use simple qualitative argument. (c) For the situation described in (b) calculate the x component of electric field at point P using the method of integration. (d) Find the angle that the electric field at P makes with x direction.

View SolutionWrite the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View SolutionA very long straight thread is oriented at right angles to an infinite conducting plane, its end is separated from the plane by a distance l. The thread carries a uniform charge of linear density λ. Suppose the point O is the trace of the thread on the plane . FInd the surface density of the induced charge on the plane
(a) at point O.
(b) as a function of a distance r from the point O.
View SolutionAn infinitely long line of linear charge density λ is shown in the figure. The potential difference VA−VB between the two points A and B is
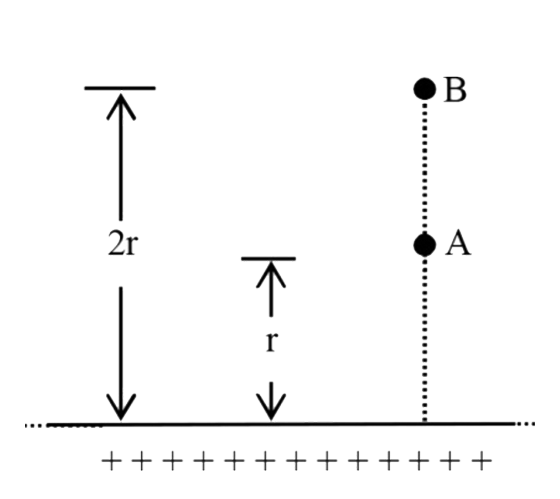
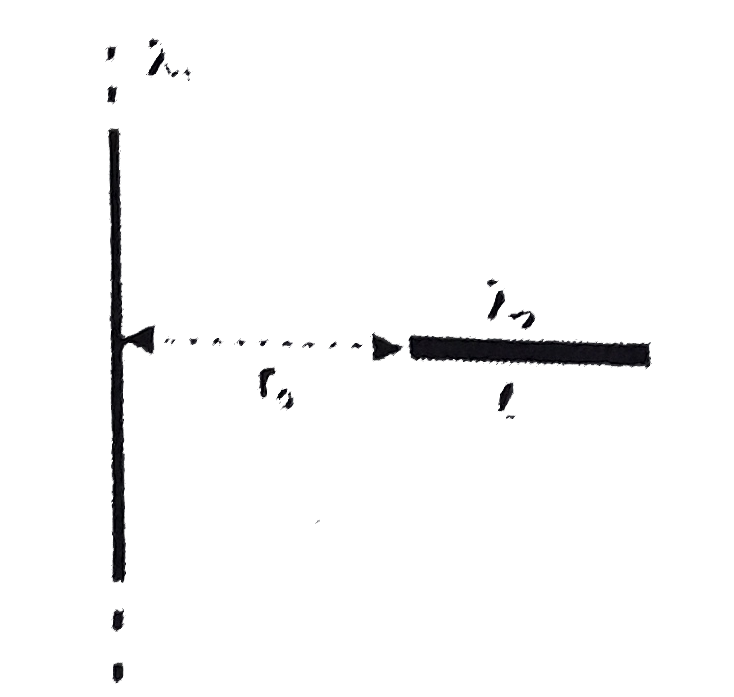
View SolutionAn infinitely long string uniformly charged with a linear charge density λ1 and a segment of length l uniformly charge with linear charge density λ2 lie in a plane at right angles to each other and separated by a distance r0 as shown in figure. The force with which these two interact is λ1λ24πε0ln(x). If l=r0, then find the value of x.
View Solution
