(a) There is an infinitely long thread uniformly charged with linear charge density λC/m. Using Gauss’ law, calculate the electric field (E0) at a distance x from the thread. (b) Now consider a semi-infinite uniformly charged thread (linear charge density =λ) as shown in figure. Find the y component of electric field at point P in terms of E0. Use simple qualitative argument. (c) For the situation described in (b) calculate the x component of electric field at point P using the method of integration. (d) Find the angle that the electric field at P makes with x direction.

The correct Answer is:(a). E0=λ2πε0x
(b). Ey=E02
(c). Ex=E02=λ4πε0x
(d). 45∘
Topper's Solved these Questions
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
Similar Questions
Three small equally charged identical conducting balls are suspended from identical insulating threads secured at one point. Length (L) of the threads is large compared to the equilibrium separation (a) between any two balls. (a) One of the balls is suddenly discharged. Find the separation between the charged balls when equilibrium is restored. Assume that the threads do not interfere and balls do not collide. (b) If two of the balls are suddenly discharged, how will the balls behave after this? Find the separation between the balls when equilibrium is restored. The threads do not interfere
View SolutionThree small equally charged identical conducting balls are suspended from identical insulating threads secured at one point. Length (L) of the threads is large compared to the equilibrium separation (a) between any two balls. (a) One of the balls is suddenly discharged. Find the separation between the charged balls when equilibrium is restored. Assume that the threads do not interfere and balls do not collide. (b) If two of the balls are suddenly discharged, how will the balls behave after this? Find the separation between the balls when equilibrium is restored. The threads do not interfere
View SolutionA short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.
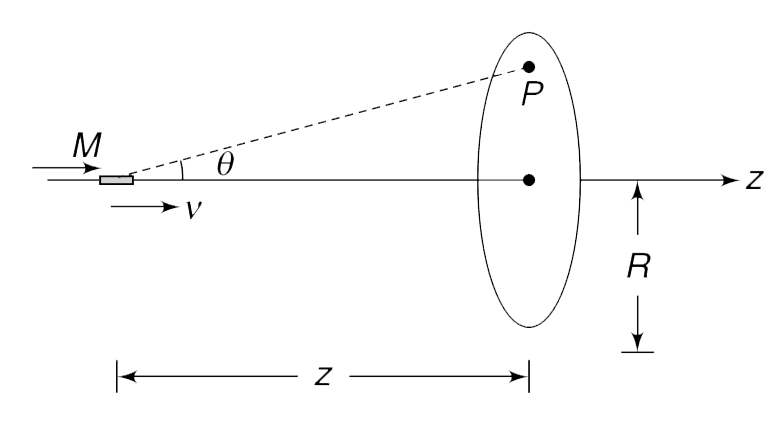
(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.
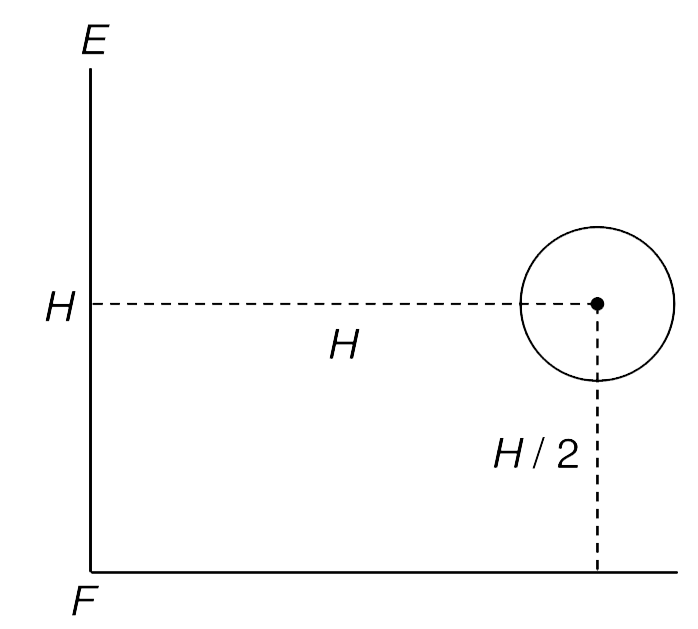
View SolutionIn the Figure FE is a man of height H standing on a floor. E is eye of the man and F is his foot. The distance between eye and the head is negligible. A steel ball of radius r is suspended in front of him. The distance of the ball from the man is H and height of the centre of the ball from the floor is H2. It is given that r<<H. The surface of the ball acts like a mirror and the man sees his image in it. Calculate the angle subtended by the image at the eye of the man.
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is lamda
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density lambda is directly proportional to
View SolutionFind electric field at point A, B, C, D due to infinitely long uniformly charged wire with linear charge density λ and kept along z-axis (as shown in figure). Assume that all the parameters are in S.l. units.

View SolutionUsing Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View Solutionएक अनन्त लम्बाई के रेखीय चालक पर एकसमान वितरित आवेश का रेखीय आवेश घनत्व λ=1×10−5 कूलाम/मीटर है। चालक से लम्बवत् 5 मीटर दूर स्थित बिन्दु पर विद्युत् क्षेत्र की तीव्रता ज्ञात कीजिए।
View SolutionFind the electric field intensity at a point P which is at a distance R (point lying on the perpendicular drawn to the wire at one of its end) from a semi-infinite uniformly charged wire. (Linear charge density = lambda ).
View SolutionFind ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density lamda is kept along z-axis:
View SolutionElectric field at a point of distance from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View Solutionएक अनन्त लम्बा रैखिक आवेश 2cm की दूरी पर 7.182×108N/C का विद्युत क्षेत्र उत्पन्न कर रहा है | रेखीय आवेश घनत्व होगा
View SolutionState Gauss' law in electrostatic. Using it derive an expression for the electric field due to an infinitely long straight wire of linear charge density lambda C/m.
View SolutionA uniformly charged rod whose length is 4cm and linear charge density lambda=30 mu C//m is, The x-component of the electric field at point P will be: -
View Solution
