Two concentric metallic spherical shells are given positive charges . Then
the outer sphere is always at a higher potential
the inner sphere is always at a higher potential
both the spheres are at the same potential
no prediction can be made about their potentials unless the actual values of charges and radii are known
The correct Answer is:2
To analyze the problem of two concentric metallic spherical shells with positive charges, we will follow these steps:
Step 1: Understand the Configuration
We have two concentric metallic spherical shells. Let's denote the inner shell as Shell 1 with radius R1 and charge Q1, and the outer shell as Shell 2 with radius R2 and charge Q2. Both charges are positive.
Hint: Remember that metallic shells distribute charge uniformly over their surfaces.
Step 2: Determine the Electric Field
The electric field E inside a conductor in electrostatic equilibrium is zero. Therefore, the electric field inside Shell 1 (at radius r<R1) is zero. For the region between the shells (i.e., R1<r<R2), the electric field due to Shell 1 can be expressed using Gauss's law.
Hint: Use Gauss's law to find the electric field in the region between the shells.
Step 3: Calculate the Potential
The electric potential V at a distance r from a charged sphere is given by the formula:
V=14πϵ0Qr
For the inner shell, the potential at its surface (at R1) is:
V1=14πϵ0Q1R1
For the outer shell, the potential at its surface (at R2) is:
V2=14πϵ0Q2R2
Hint: Remember that the potential outside a charged shell is the same as if all the charge were concentrated at the center.
Step 4: Compare the Potentials
Since both shells are positively charged, we need to compare V1 and V2. The potential inside the outer shell (at R2) is influenced by both charges. Therefore, the total potential at R2 is:
Vouter=V2+14πϵ0Q1R2
Since R1<R2, the term Q1R1 will be greater than Q1R2. Thus, the potential at the inner shell will be greater than that at the outer shell.
Hint: Compare the denominators when evaluating the potentials.
Step 5: Conclusion
From the analysis, we conclude that the potential on the inner surface (Shell 1) is greater than the potential on the outer surface (Shell 2). Therefore, the inner shell is at a higher potential than the outer shell.
Final Answer: The potential of the inner shell is greater than that of the outer shell.
We have two concentric metallic spherical shells. Let's denote the inner shell as Shell 1 with radius R1 and charge Q1, and the outer shell as Shell 2 with radius R2 and charge Q2. Both charges are positive.
The electric field E inside a conductor in electrostatic equilibrium is zero. Therefore, the electric field inside Shell 1 (at radius r<R1) is zero. For the region between the shells (i.e., R1<r<R2), the electric field due to Shell 1 can be expressed using Gauss's law.
The electric potential V at a distance r from a charged sphere is given by the formula:
V=14πϵ0Qr
For the inner shell, the potential at its surface (at R1) is:
V1=14πϵ0Q1R1
For the outer shell, the potential at its surface (at R2) is:
V2=14πϵ0Q2R2
Since both shells are positively charged, we need to compare V1 and V2. The potential inside the outer shell (at R2) is influenced by both charges. Therefore, the total potential at R2 is:
Vouter=V2+14πϵ0Q1R2
Since R1<R2, the term Q1R1 will be greater than Q1R2. Thus, the potential at the inner shell will be greater than that at the outer shell.
From the analysis, we conclude that the potential on the inner surface (Shell 1) is greater than the potential on the outer surface (Shell 2). Therefore, the inner shell is at a higher potential than the outer shell.
Topper's Solved these Questions
Similar Questions
There are three concentric metallic spherical shells of radius R, 2R and 3R. Charge Q is given to the innermost spherical shell. If the innermost spherical shell is connected with a metal wire to the outermost spherical shell without touching the middle shell, which is connected to the earth, then, find charges appearing on all surfaces.
View SolutionAssertion: Two concentric charged spherical shells are given. The potential difference between the shells depends on charge of inner shell.
Reason: Potential due to charge of outer shell remains same at every point inside the sphere.View Solution
Knowledge Check
- Question 1 - Select One
Two conducting concentric spherical shells are given positive charges. Choose the correct outcome.
AOuter shell will be at higher potentialBInner shell will be at higher potentialCOuter will always be at higher potential irrespective of the sign of charges given to two spheresDNo prediction can be made using the given data - Question 2 - Select One
There are two concentric spherical shells with inner shell having positive charge q and outer shell having a charge -q. Now outer shell is supplied a charge -2g and inner shell is earthed, Calculate the ratio of initial and final capacities of the system. (If a = 3R, b= 5 R)
 A3/5B3C1D5/3
A3/5B3C1D5/3 - Question 3 - Select One
Three concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
A1:2:3B1:3:5C1:4:9D1:8:18
Three concentric metallic spherical shells of radii R, 2R, 3R, are given charges Q1, Q2, Q3, respectively. It is found that the surface charge denisties on the outer surfaces of the shells are equal. Then, the ratio of the charges given to the shells, Q1:Q2:Q3, is
View SolutionTwo concentric spherical shells of radii R and 2R are given charges Q1andQ2 respectively.
The surfaces charge densities of the outer surfaces are equal. Determine the ratio Q1:Q2.View SolutionA metallic spherical shell of radius r1 is surrounded by another concentric metallic spherical shell of radius r2. The space between the two shells is filled with a dielectric of dielectric constant K. If a charge Q is given to the inner shell, the charge appearing on the outer surface of the outer shell is
View SolutionA and B are two concentric spherical shells. If A is given a charge +q while B is earthed as shown in figure then
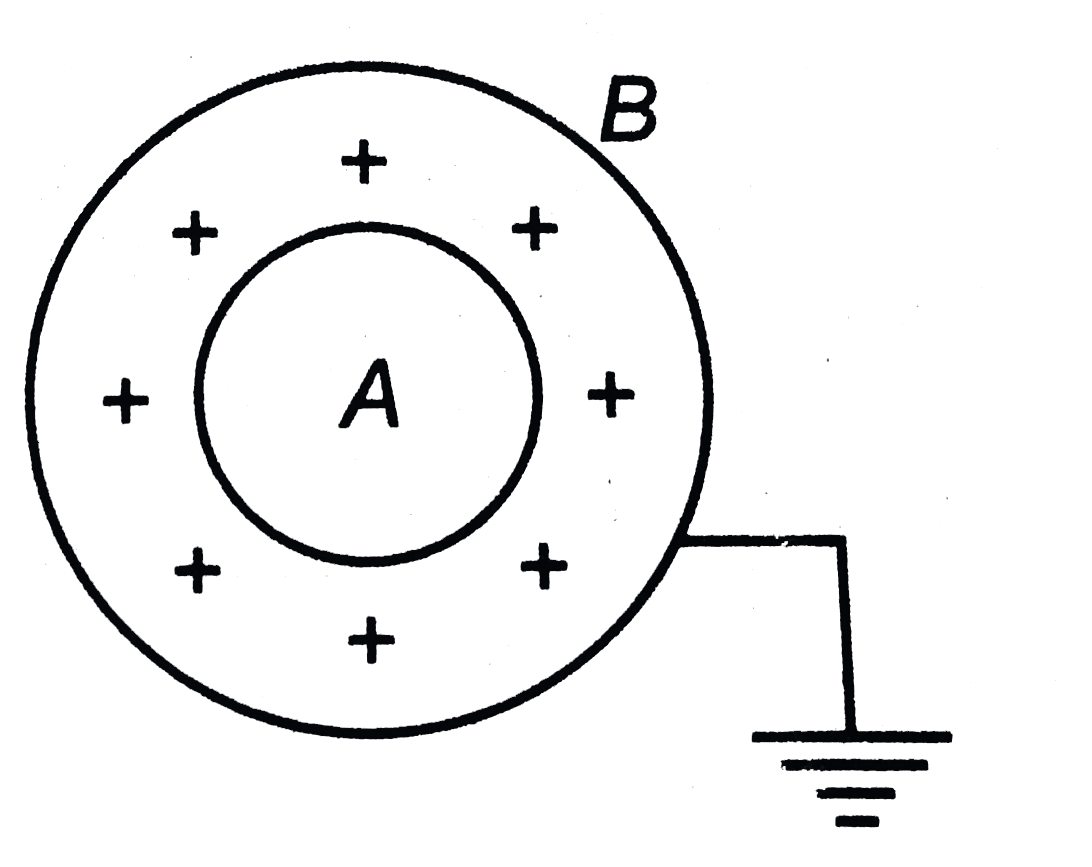 View Solution
View SolutionThree concentric metallic spherical shells A,B and C of radii a,band c(a<b<c) have surface charge densities −σ,+σand -sigma respectively,thepotentialofshellA is
View Solution

