(a) Find the value of i and potential difference across each cell.
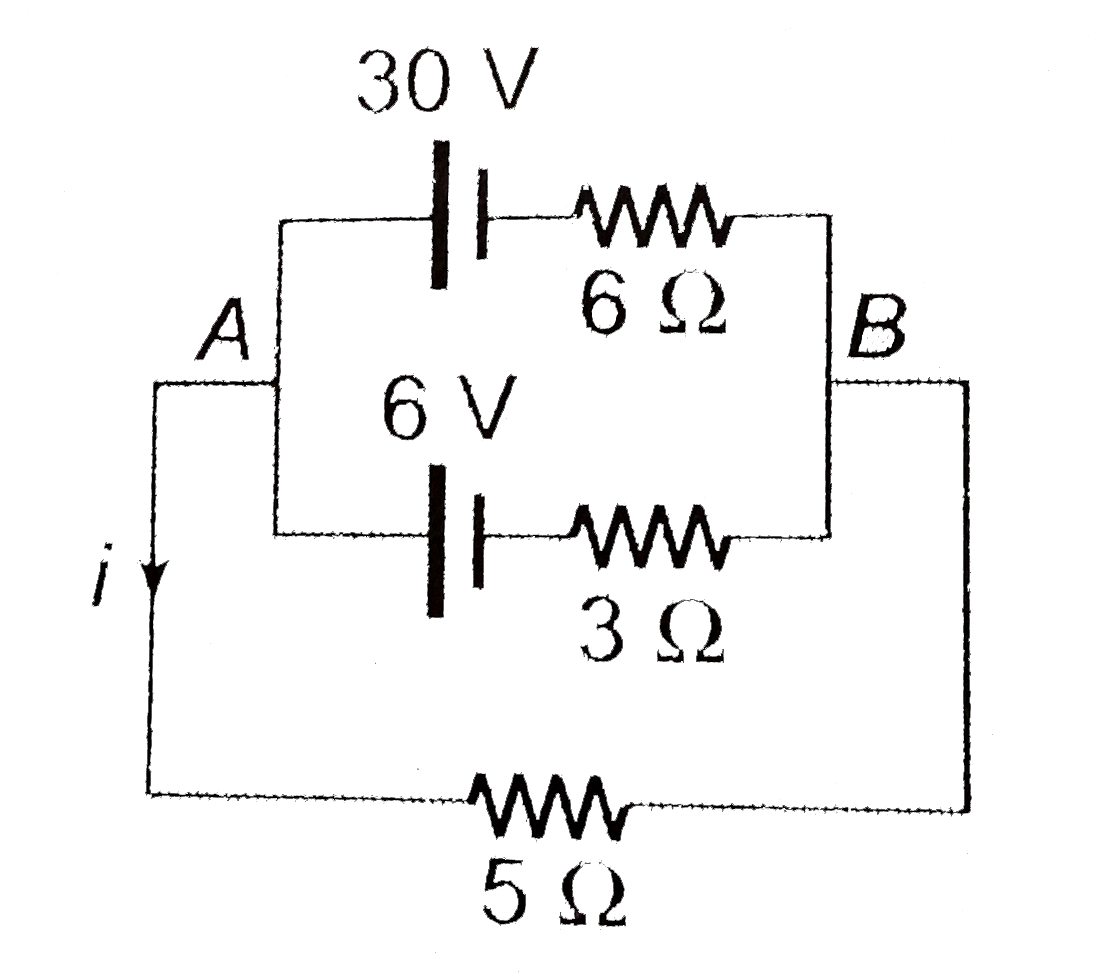
(b) Find potential difference between A and B.
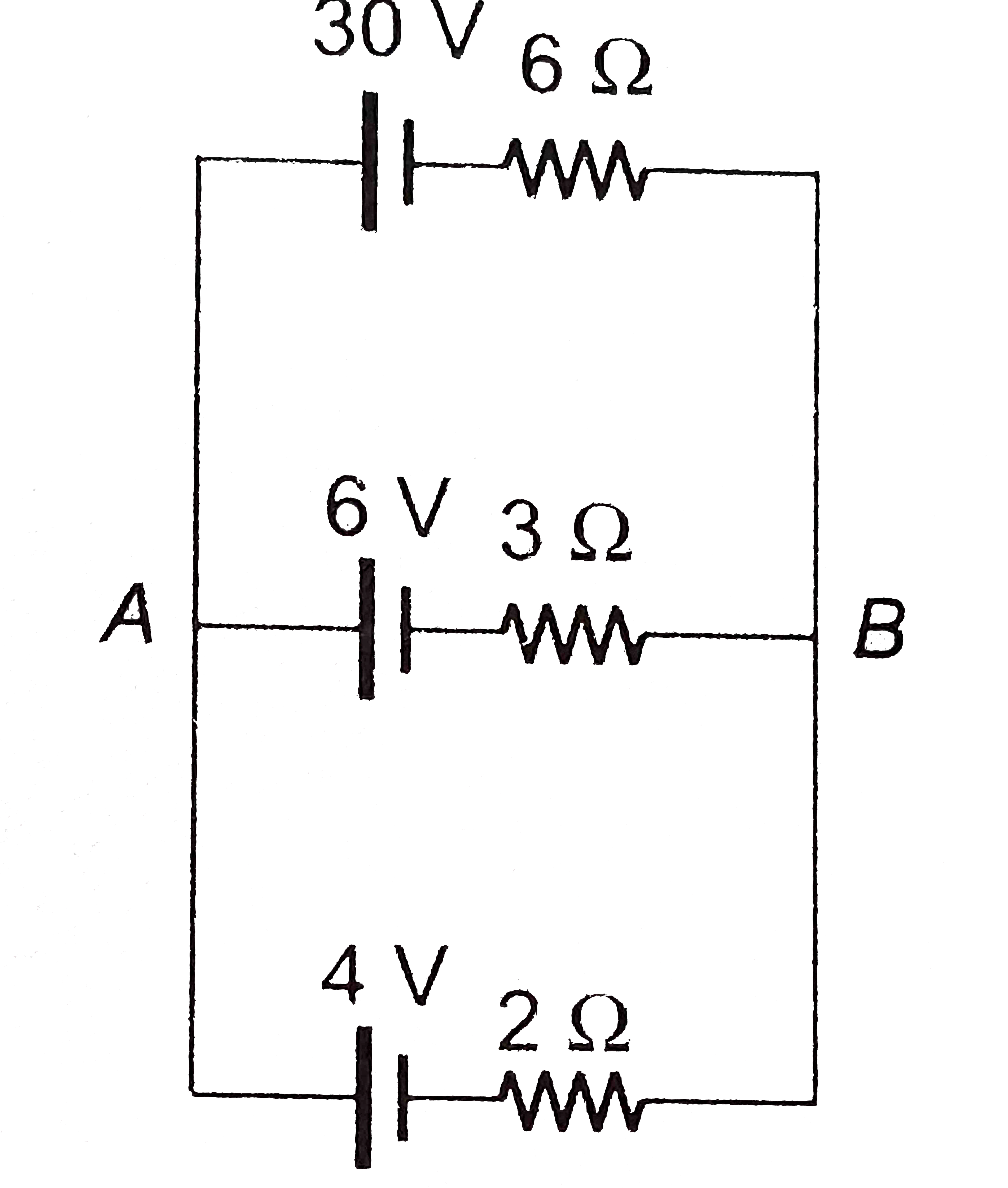
( c) In the given circuit,
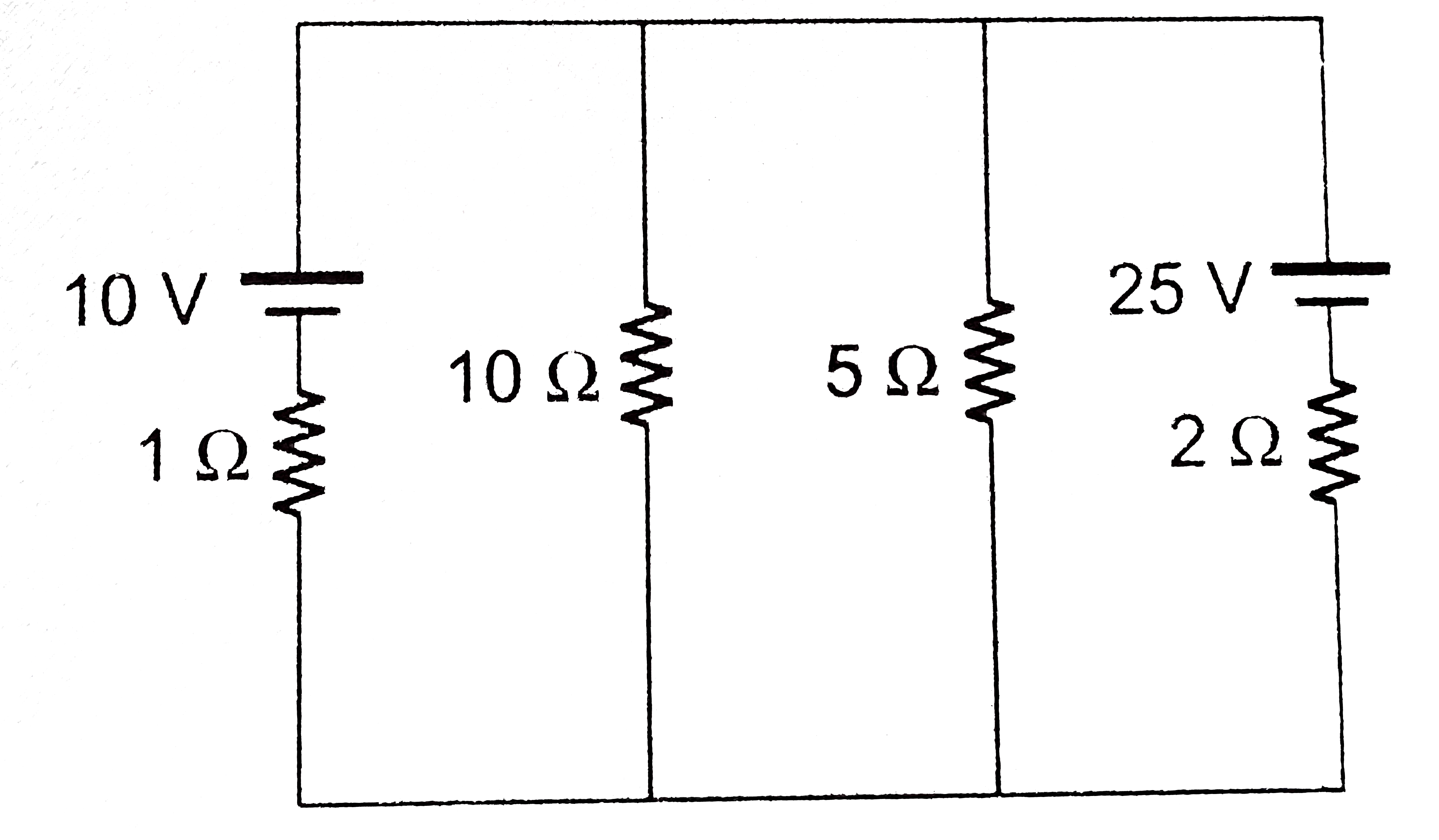
find
(i) potential difference between terminals 10V cell
(ii) current through 25V cell
(iii) current through 5Ω
(d) Find the current through resistance 5Ω.
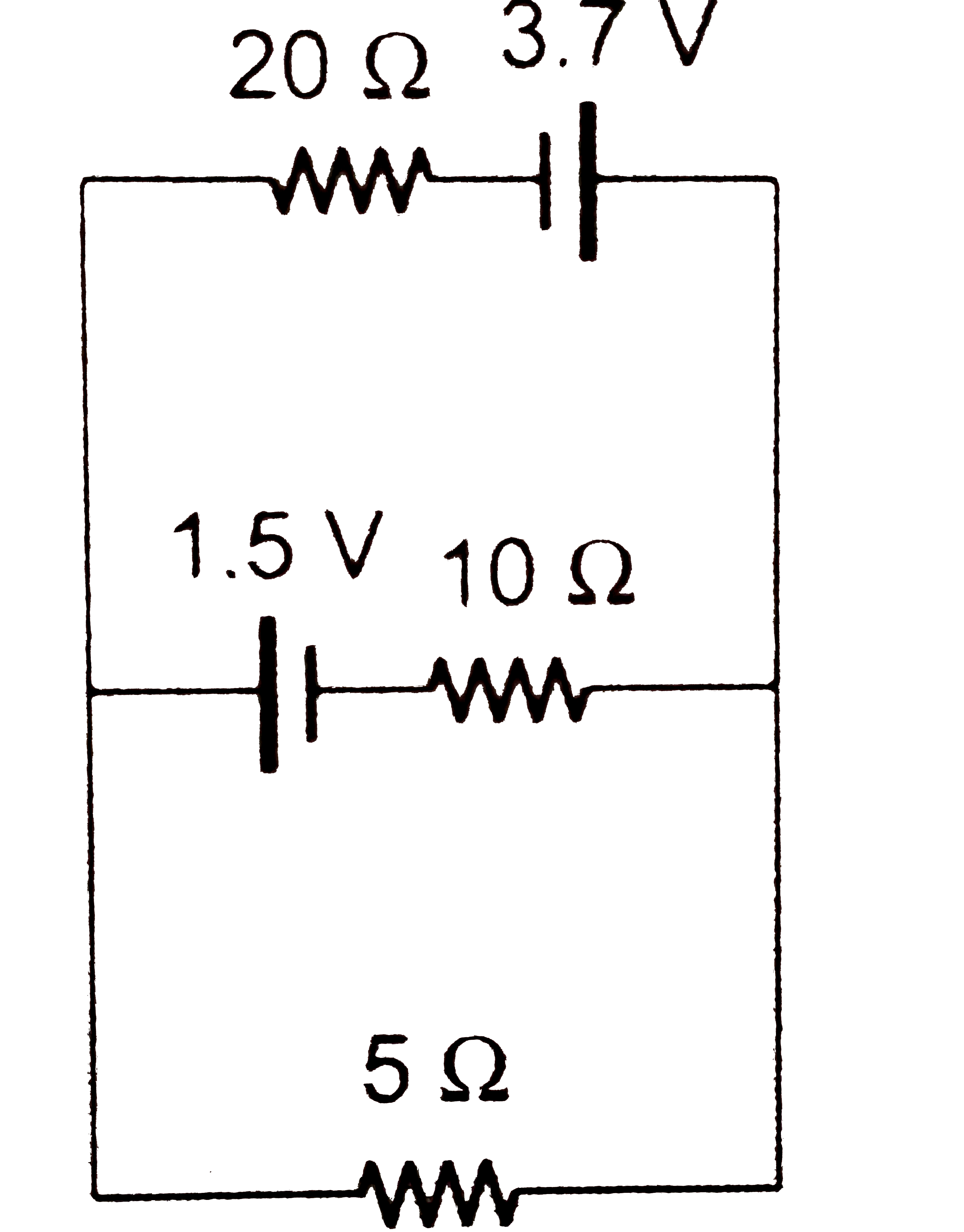 .
.
(a) 
By Kirchhoff's rules :First assume direction of currents in different branches as you like but currents should be balanced at junctions. Here current in 5Ω is required and it is i. Let current in 30V cell is i1 towards left.
At junction A:i=i1+x⇒x=i−i1 i.e., current in 6V cell is i−i1 towards left.
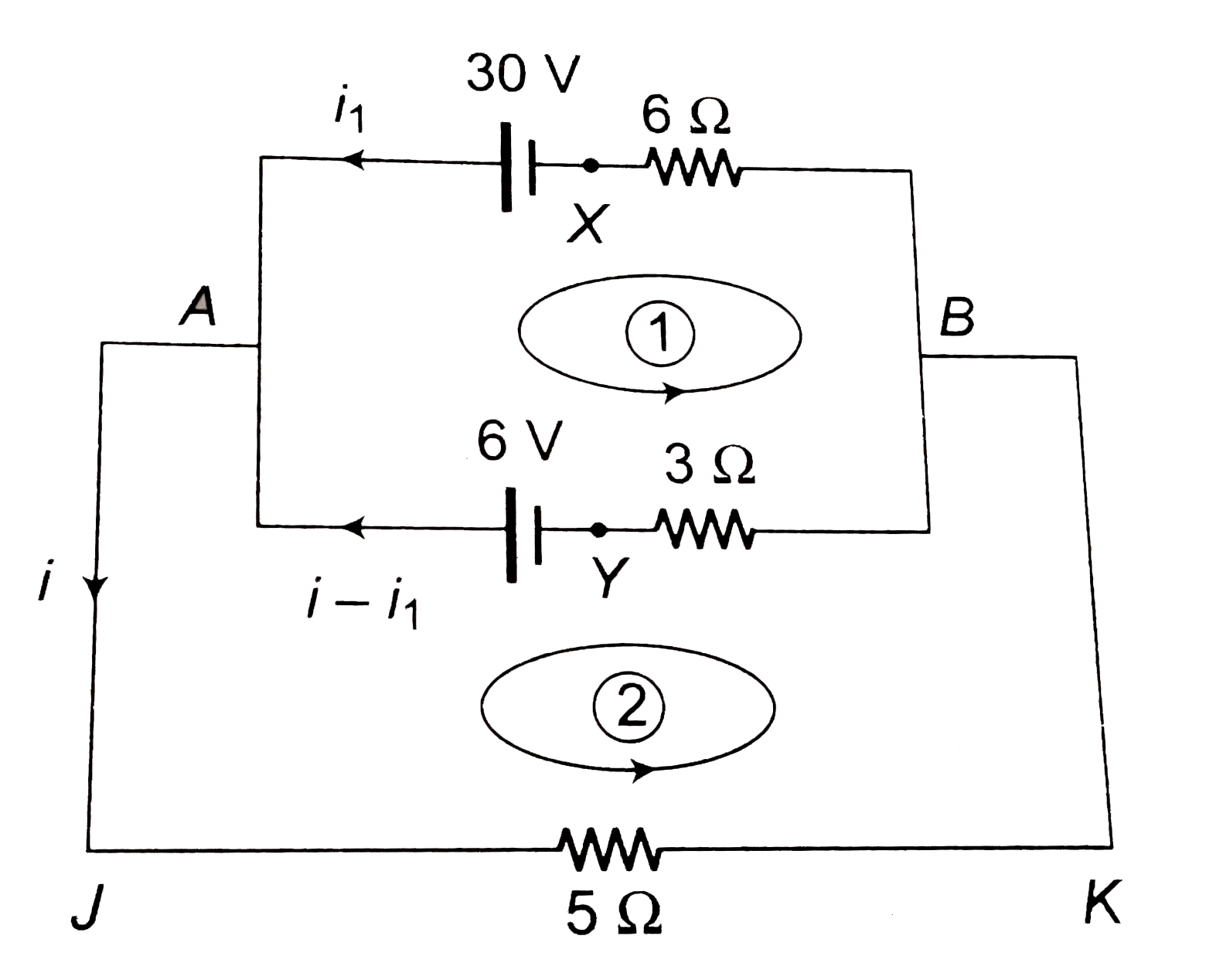
Here two unknowns i and i1, so we require two equations. For this move from one point to the same point on two different paths.
(a) A→A,loop①,pathAYBXA
VA−6+3(i−i1)−6i1+30=VA
3i−3i−6i1=−24
i−3i1=−8 ...(i)
(ii) A→A,loop②,path AJKBYA
VA−i×5−(i−i1)×3+6=VA
−8i+3i1=−6
8i−3i1−6 ...(ii)
Solving (i) and (ii) rArr (i)-(ii) ⇒−7i=−14⇒i=2A

VA−VB=2×5=10V
Alternative method :
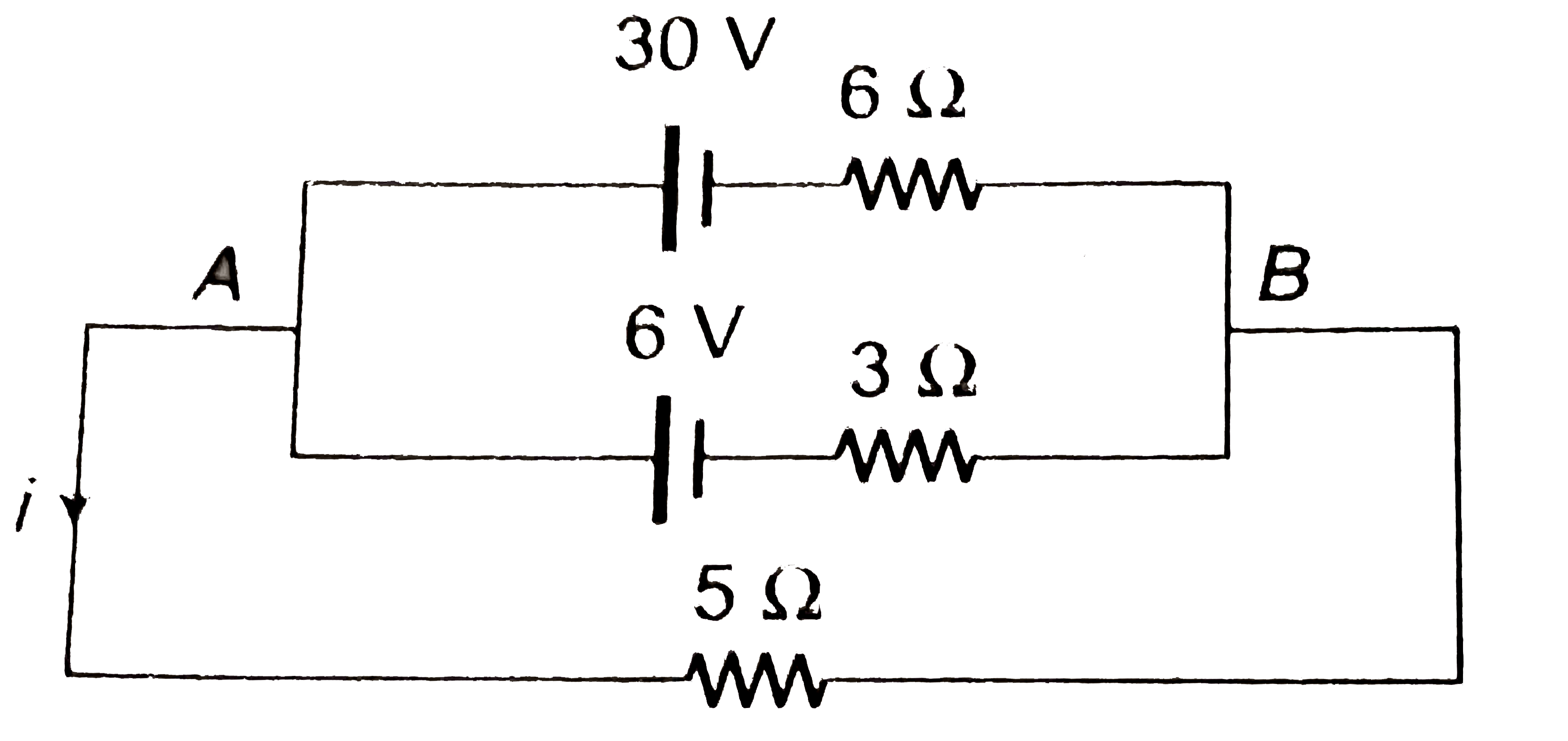
Here, one terminal of cells is connected to A and another terminal is connected to B (do not look at internal resistance of cells), hence these cells can be replaced by single cell.
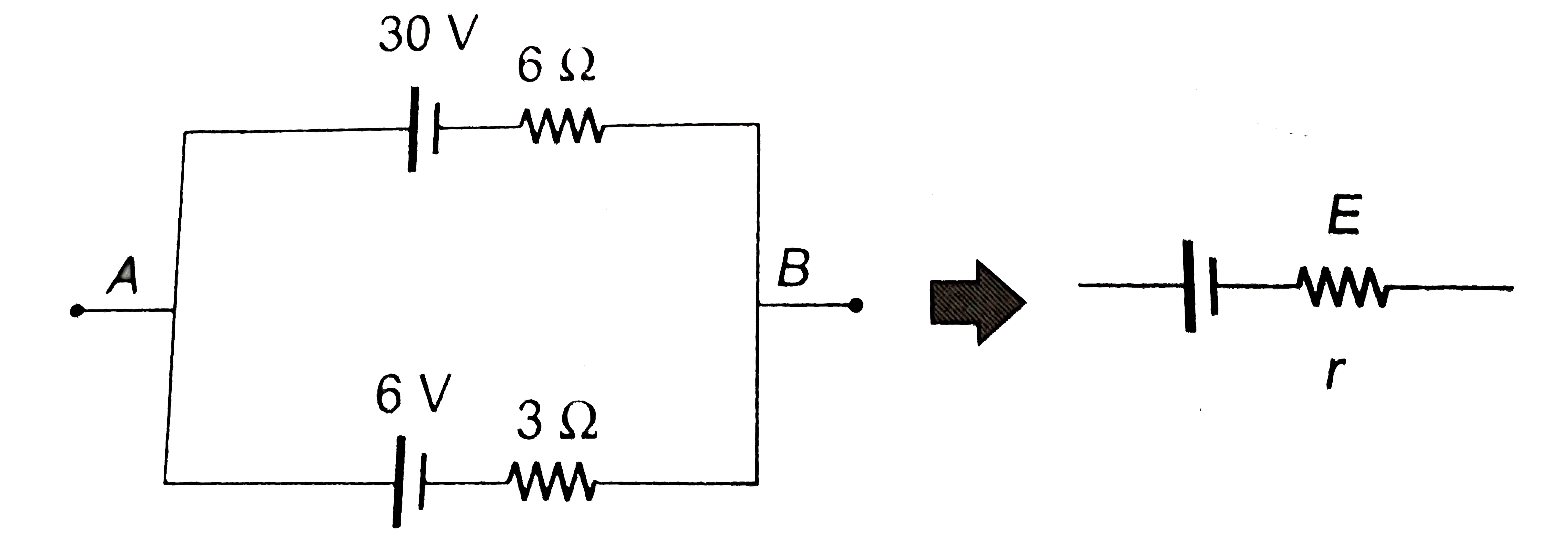
E=E1r1+E2r21r1+1r2=36+6316+13=5+212=14V
r=r1r2r1+r2=3×63+6=2Ω.
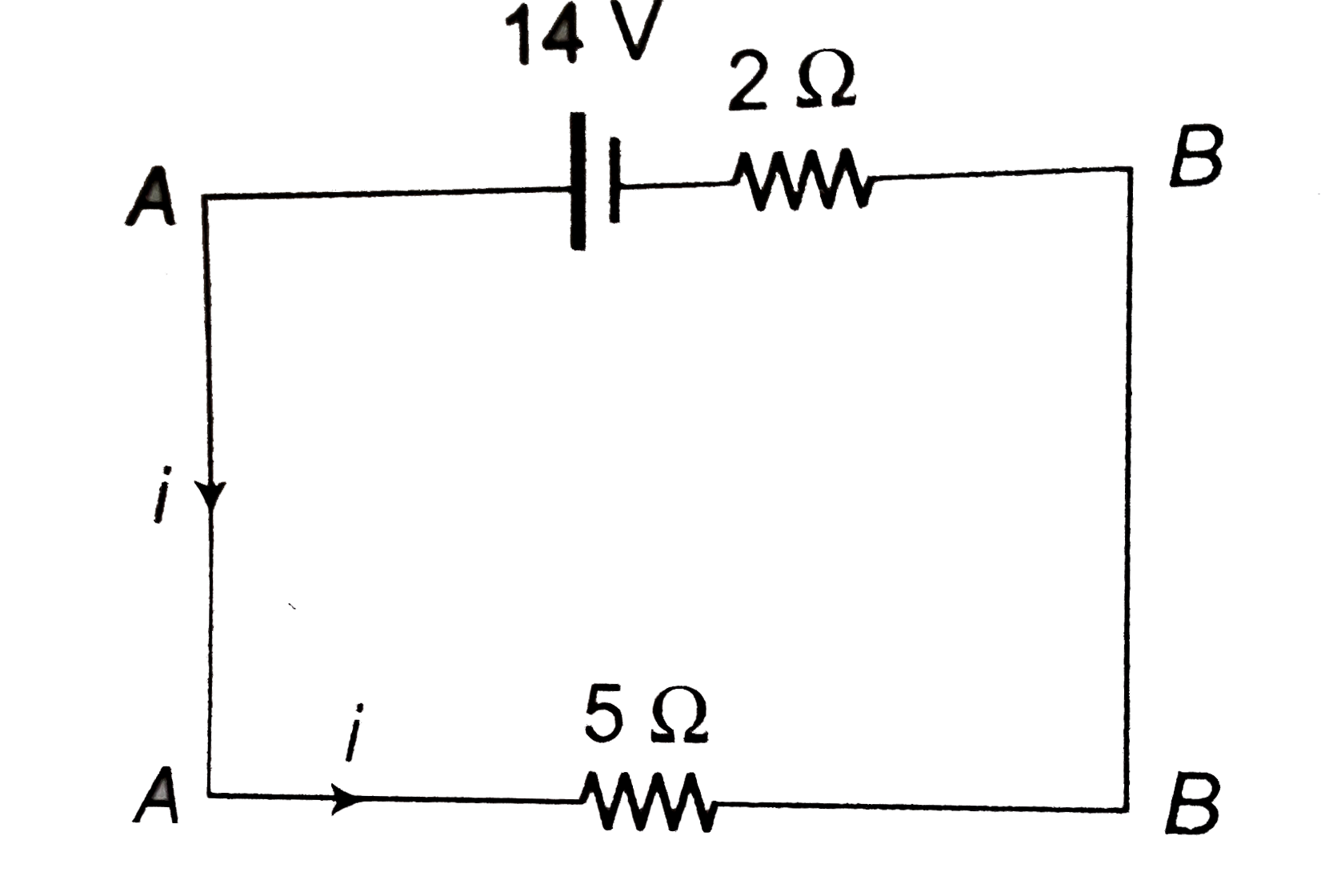
i=142+5=2A
VA−VB=i×5=2×5=10V
OR
VA−VB=14−2×2=10V
For calculating currents in other braches :

VA−VB=10V
Cell of emf 30V :
VA−VB=30−i1×6
10=30−6i1⇒i1=103A
Cell of emf 6V :
VA−VB=6−i2×3
10=6−3i2⇒i2=−43A
−ve sign indicates that current is flowing in opposite direction.
Check : i1+i2=i
103−43=2=i O.K.

Let the current flowing in 30V cell is i1 and 6V cell is i2. Current in 4V will be i1+i2 as shown
Loop①,A→A,pathAXYBA
VA−4−(i1+i2)×2−3i2+6VA
−2i1−5i2+2=0
2i1+5i2=2
Loop②,A→A,pathAUVBA
VA−30+6i1−3i2+6=VA
6i1−3i2=24
2i1−i2=8
Solving (i) and (ii), (i)-(ii), we get
6i2=−6⇒i2=−1A
2i1−(−1)=8⇒i1=7/2=3.5A
A to B :
VA−VB=6−i2×3=6−(−1)×3=8V.
Alternative method :
Here one terminal of all cells at point A and another terminal of all cells at point B, hence these cells can be replaced by single cell.
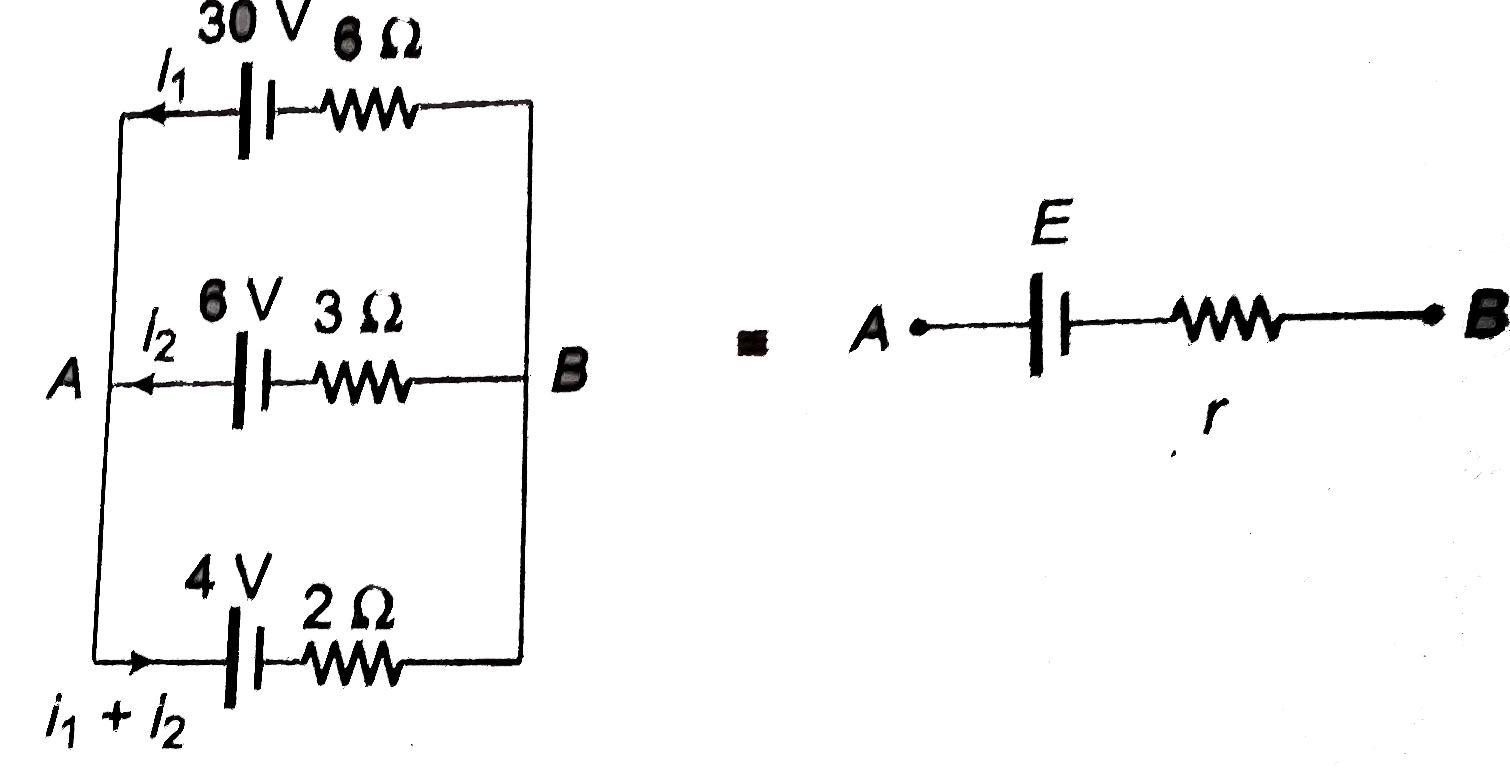
E=E1/r1+E2/r2+E3/r31r1+1r2+1r3=30/6+6/3+4/21/6+1/3+1/2
=5+2+21=9V
1r=1r1+1r2+1r3=16+13+12=1⇒r=1Ω
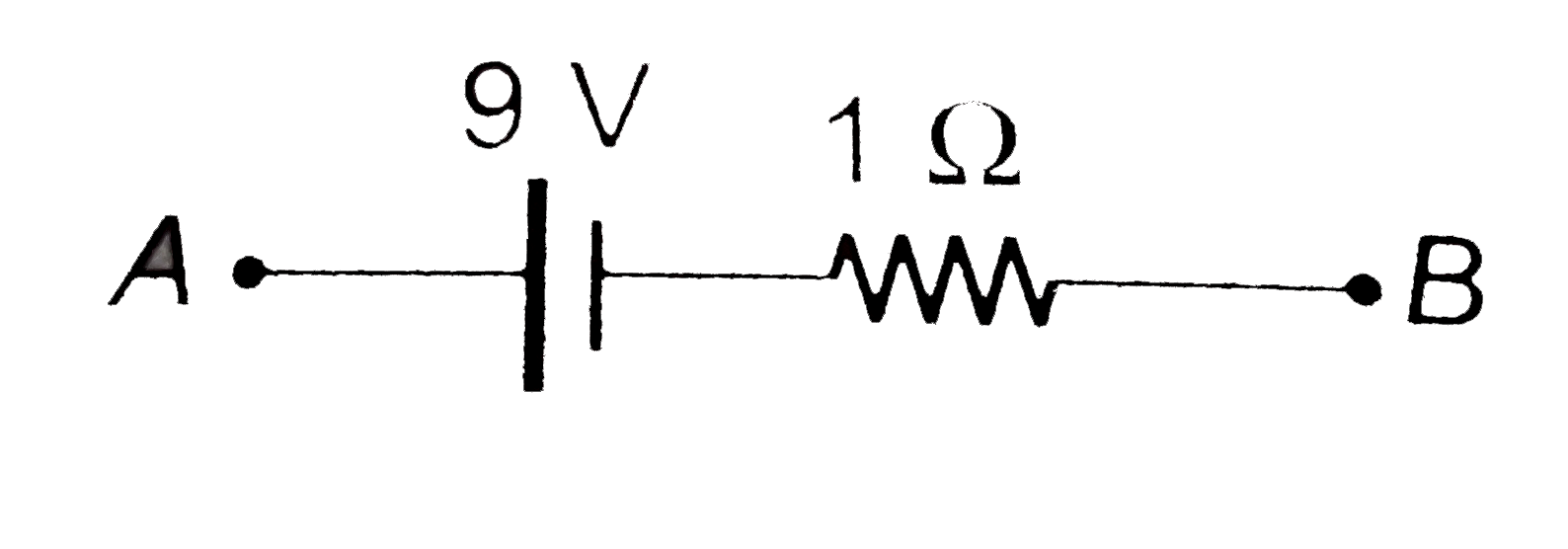
The equivalent cell is open circuit hence no current flows in it.
VA−VB=9V
Current on cells :
30V:VA−VB=30−i1×6⇒9=30−6i1
⇒i1=3.5A
6V:VA−VB=6−i1×3⇒9=6−3i2⇒i2=−1A
4V:i1+i2=3.5−1=2.5A.
( c) 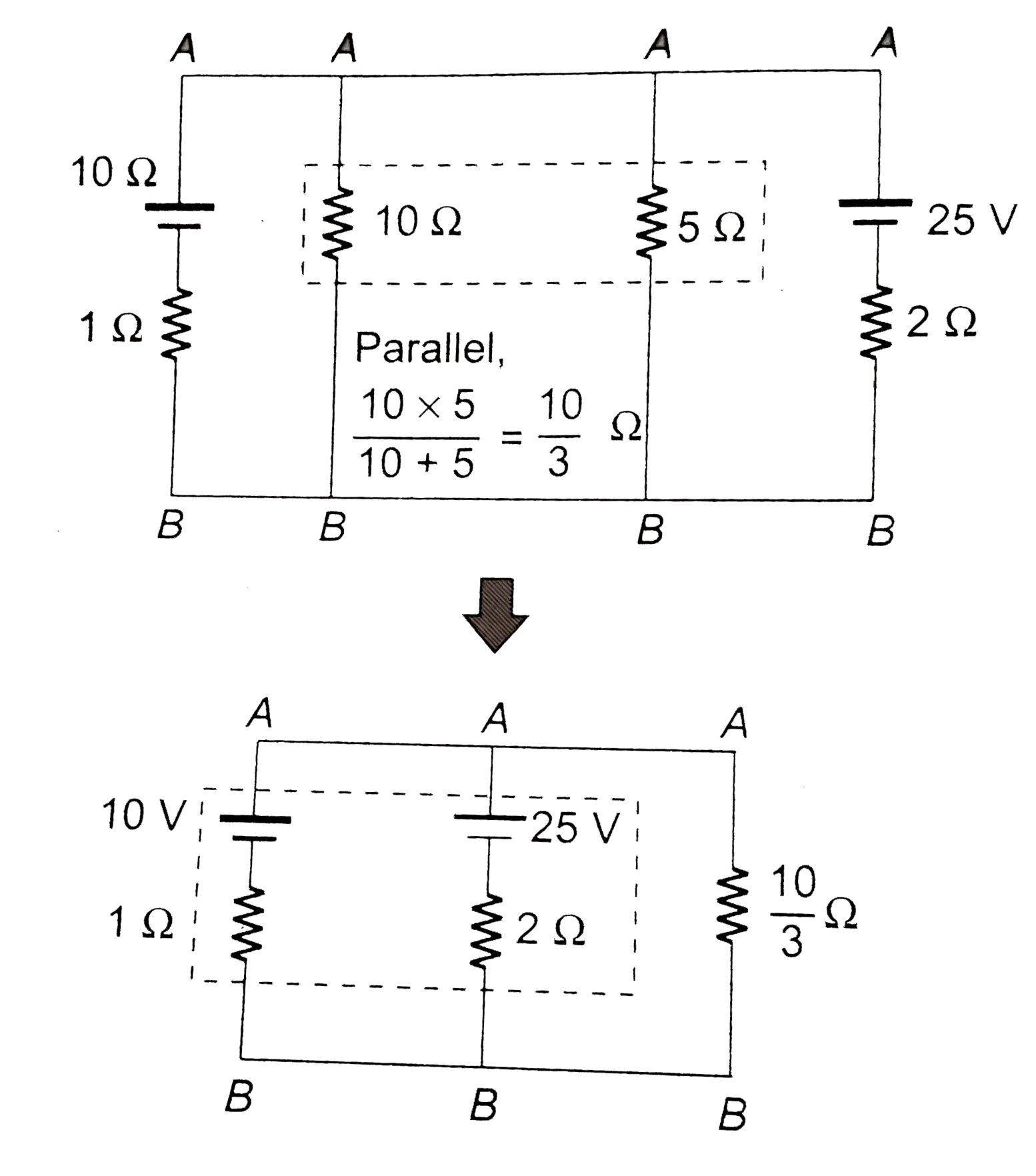
E=101+25211+12=15V
r=1×21+2=23Ω
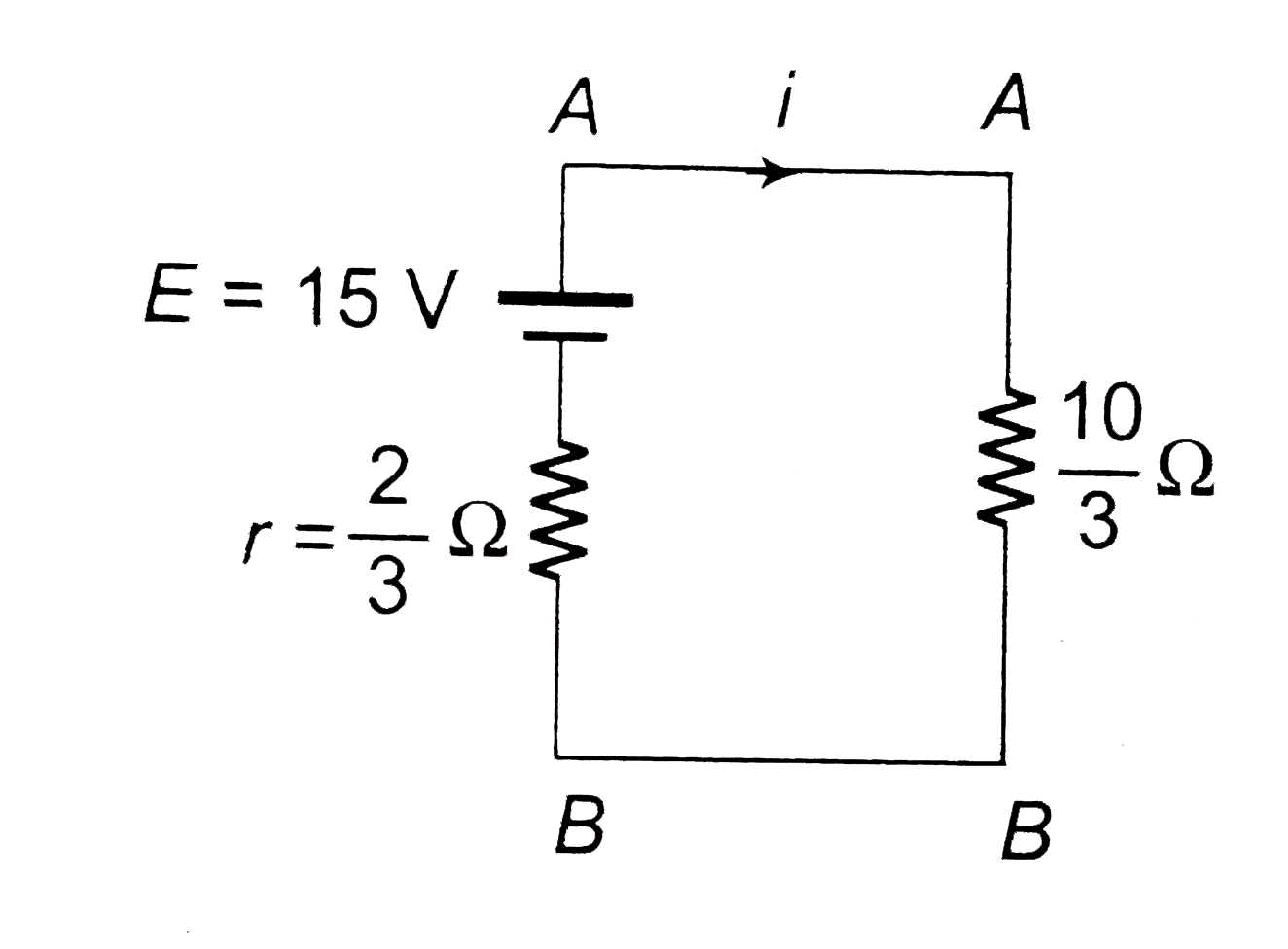
i=1523+103=154=3.75A
VA−VB=i×103=154×103=504V

(i) p.d. between terminals of 10V cell : VA−VB=504V
(ii) Let current through 25V cell is i0
VA−VB=25−i0×2
504=25−2i0
i0=508=6.25A
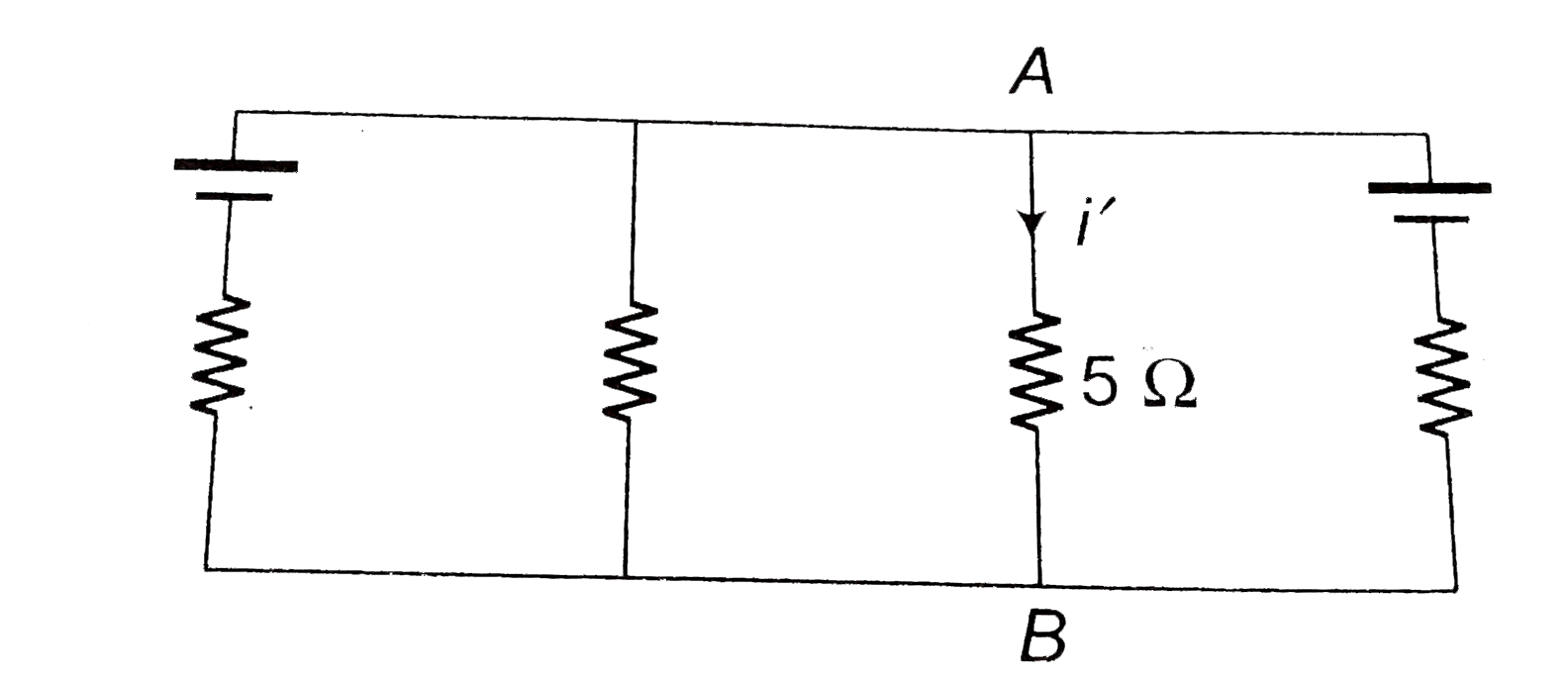
(iii) Current in 5Ω
VA−VB=i'×5
504=5i'⇒i'=2.5A
(d) 
E=3.720−1.510120+110=0.73V
r=20×1020+10=203Ω
i=0.7/320/3+5=0.735=120A.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the circuit shown in figure potential difference between point A and B is 16V. Find the current passing through 2Ω resistance.
 A1.5AB3.5AC1.0AD2.5A
A1.5AB3.5AC1.0AD2.5A
Find potential difference across the resistance 300 Ω in A and B.
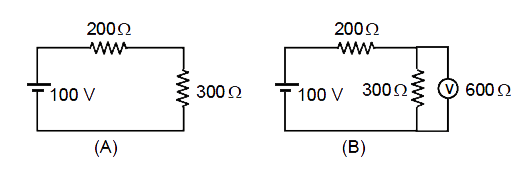 View Solution
View SolutionFind potential difference across the resistance 300Ω in A and B.
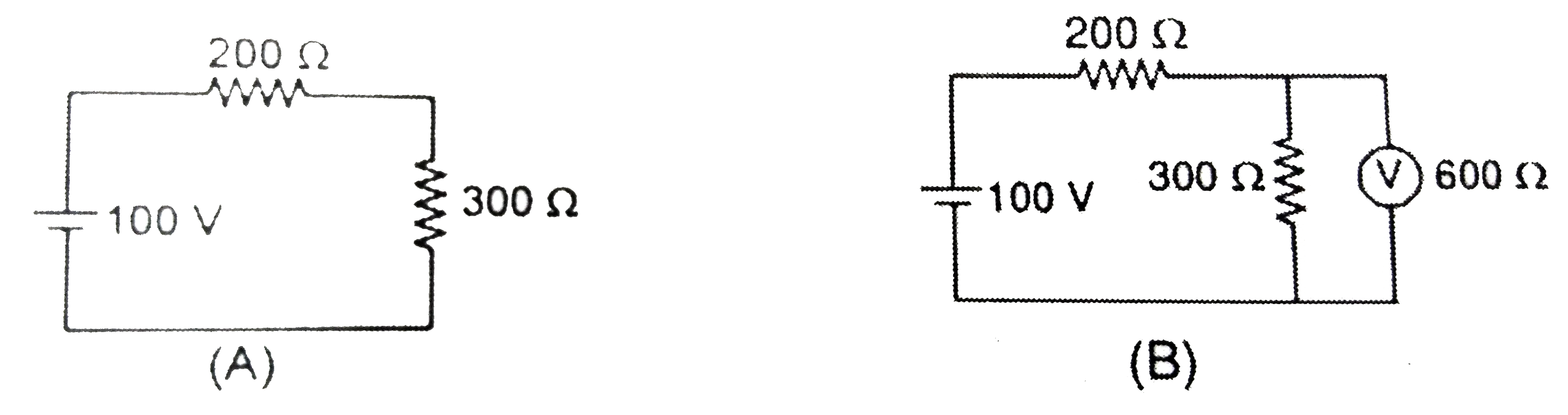 View Solution
View SolutionFind the potential difference between the points a and b. If the points a and b are joined by a resistance of 5Ω, calculate the current through this resistance.
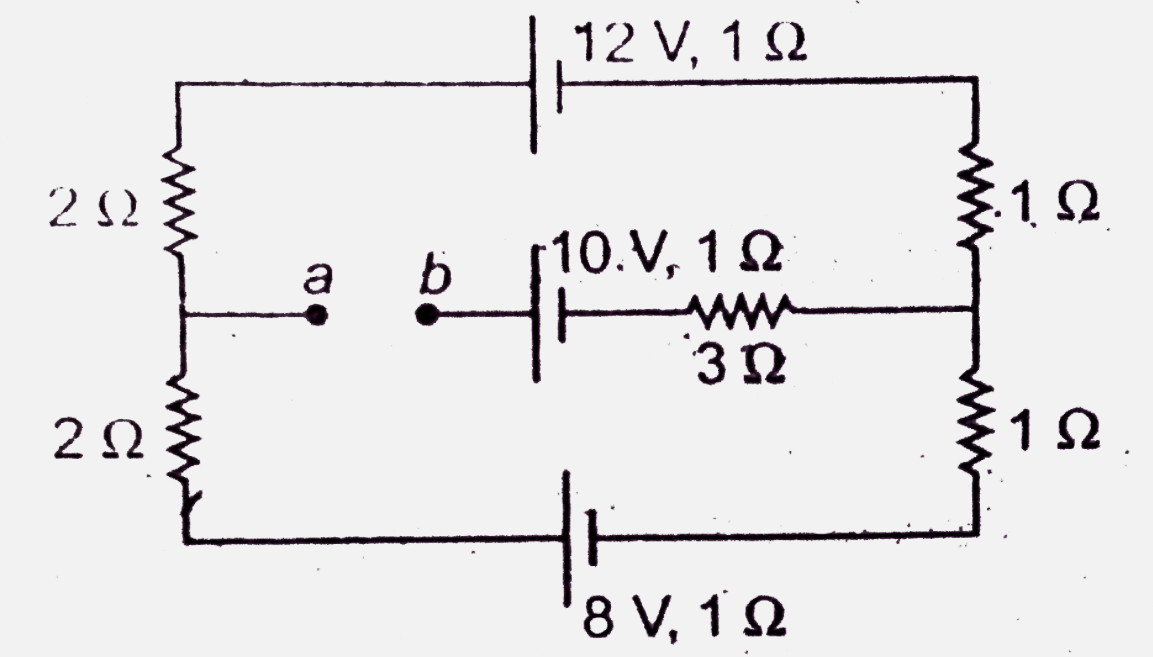 View Solution
View SolutionFor the given circuit find out:-
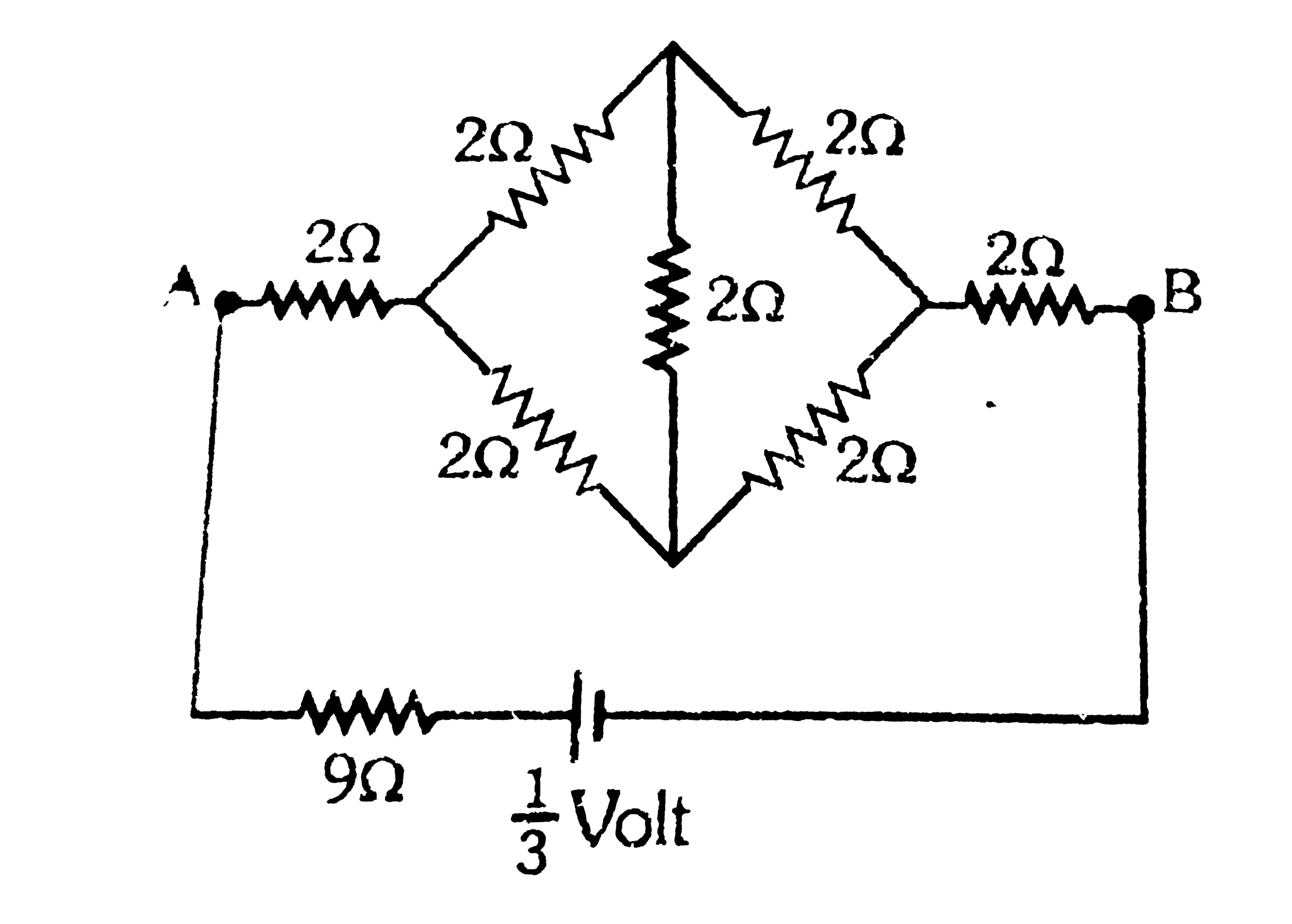
(a) Total resistance of circuit across battery terminals.
(b) Potential difference between A and B.View Solution(a) Find the potential difference between A and B
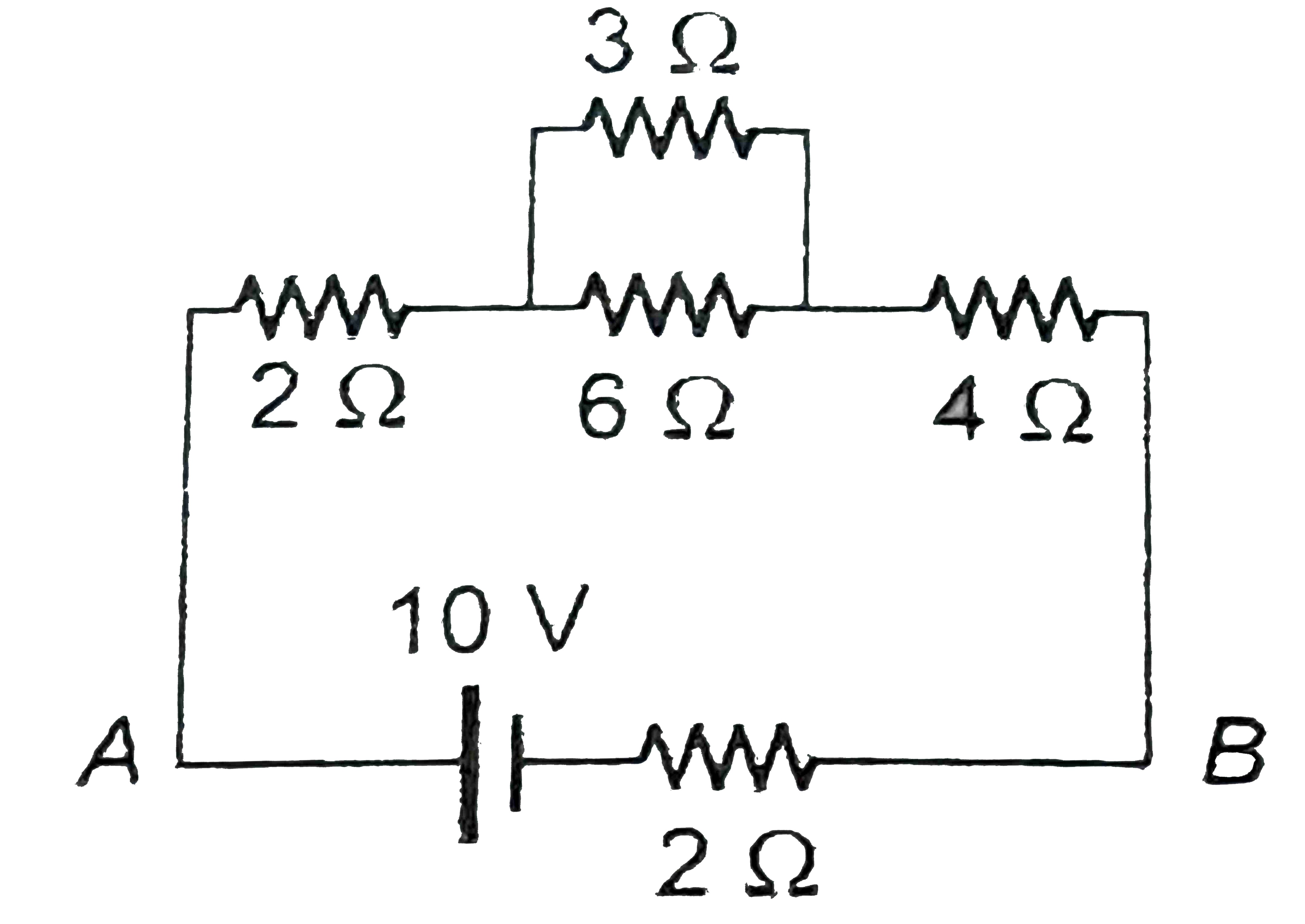
(b) Calculate the current flowing in the circuit and the potential difference across terminals of each cell.
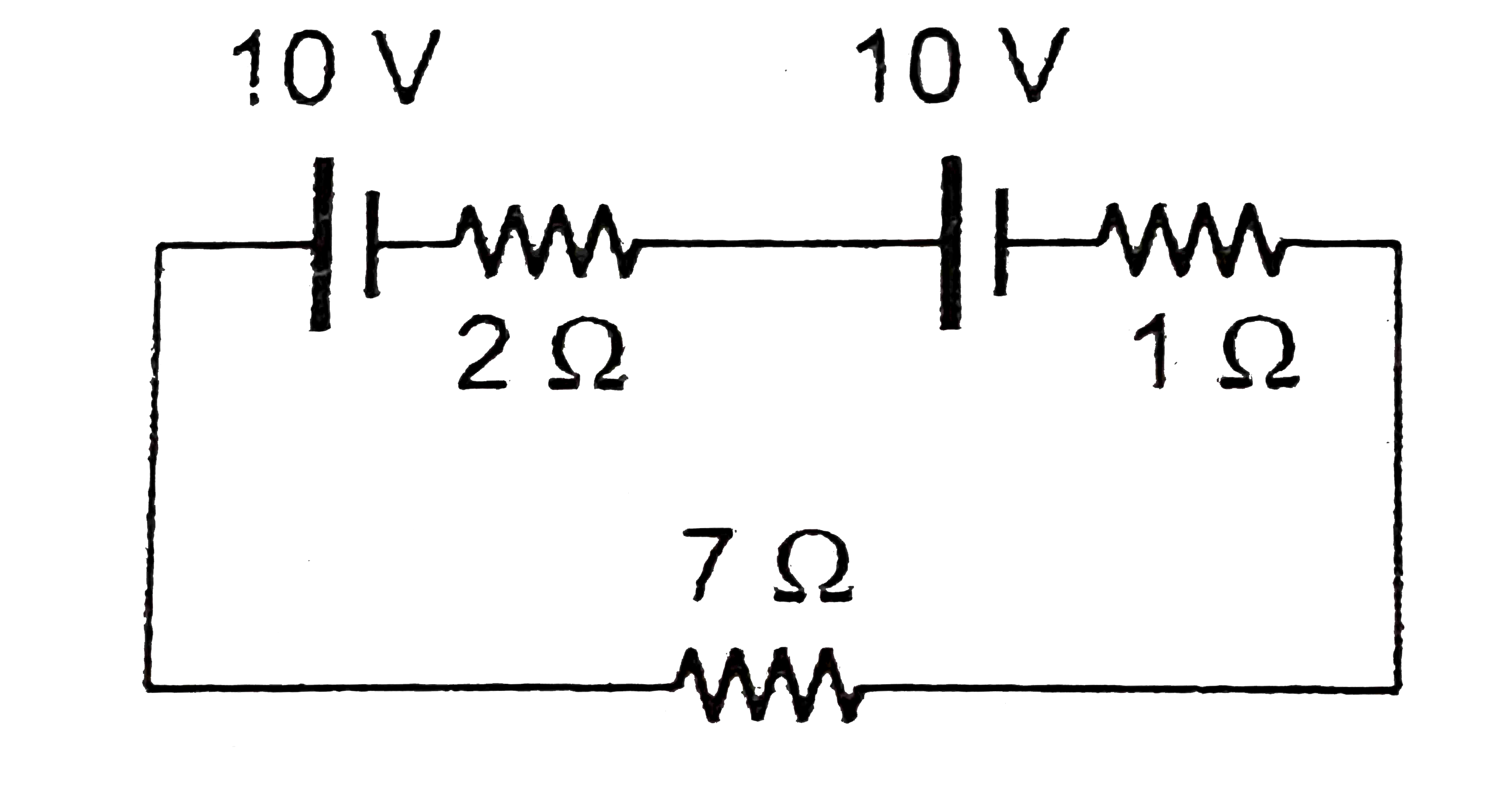
( c) Calculate the potential difference across terminals of each cell.
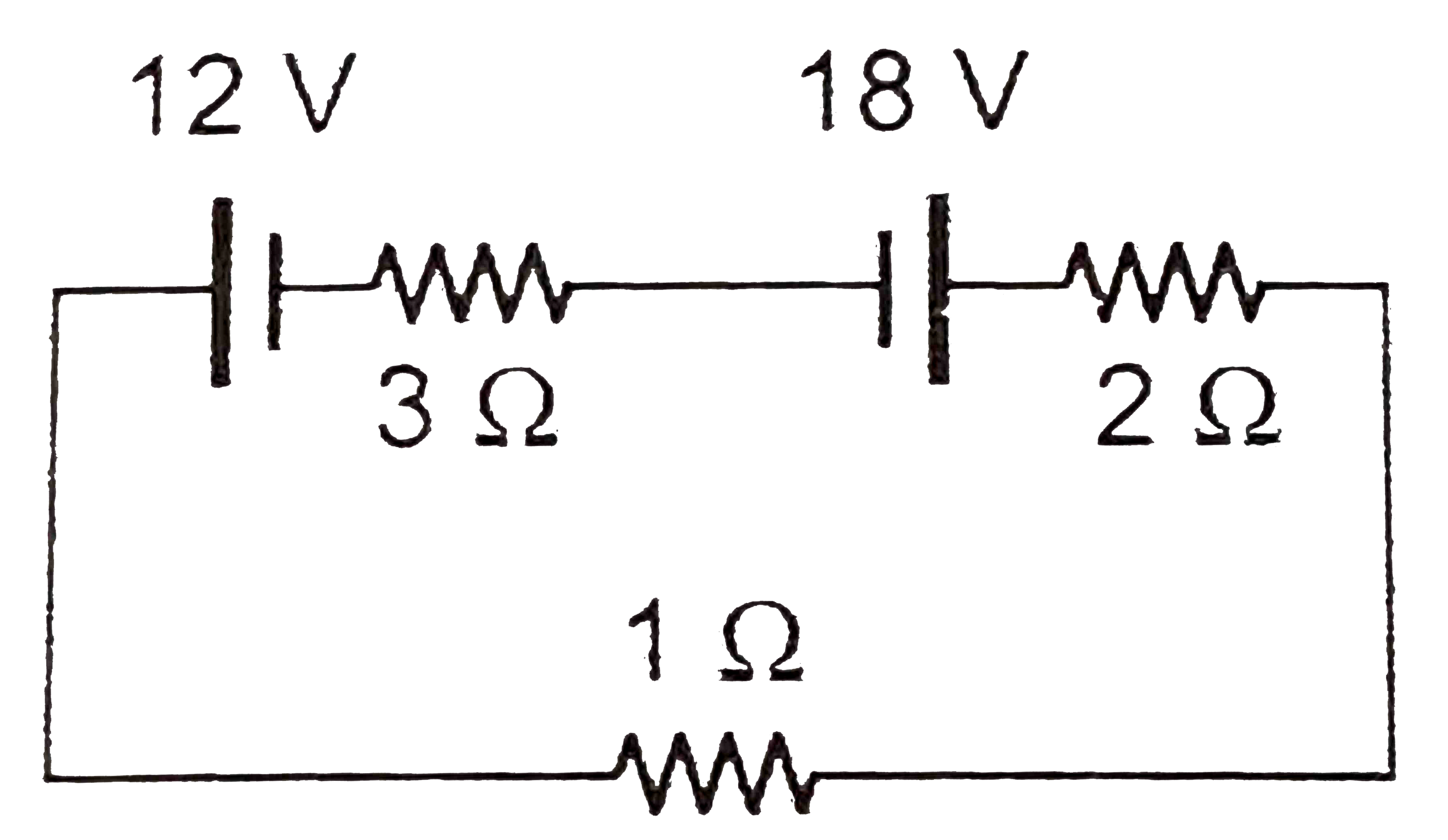
(d) Calculate the potential difference between A and B
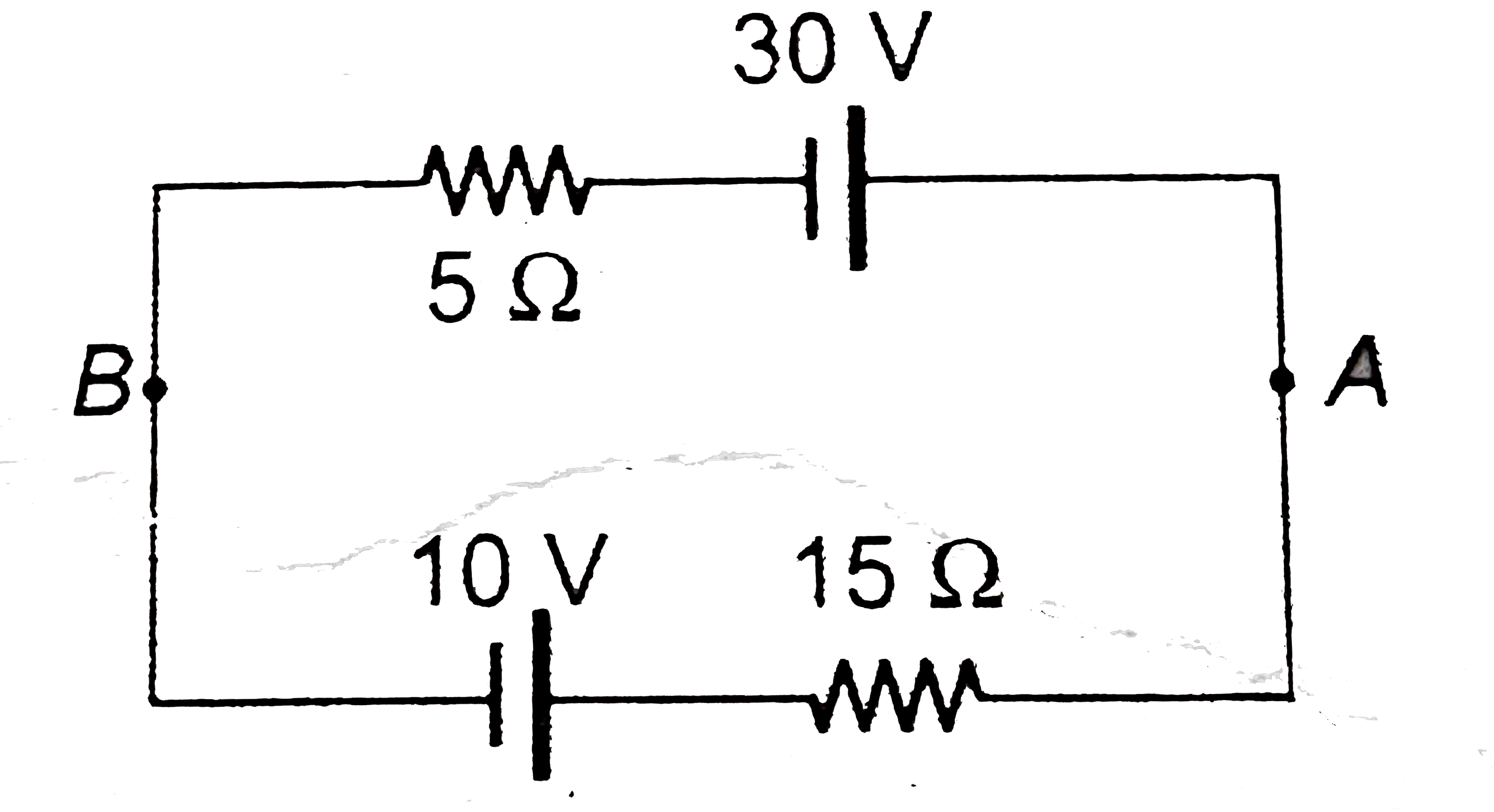
( e) Calculate the current in each resistor and terminal potential difference across each cell.

(f) Calculate potential difference across each cell.
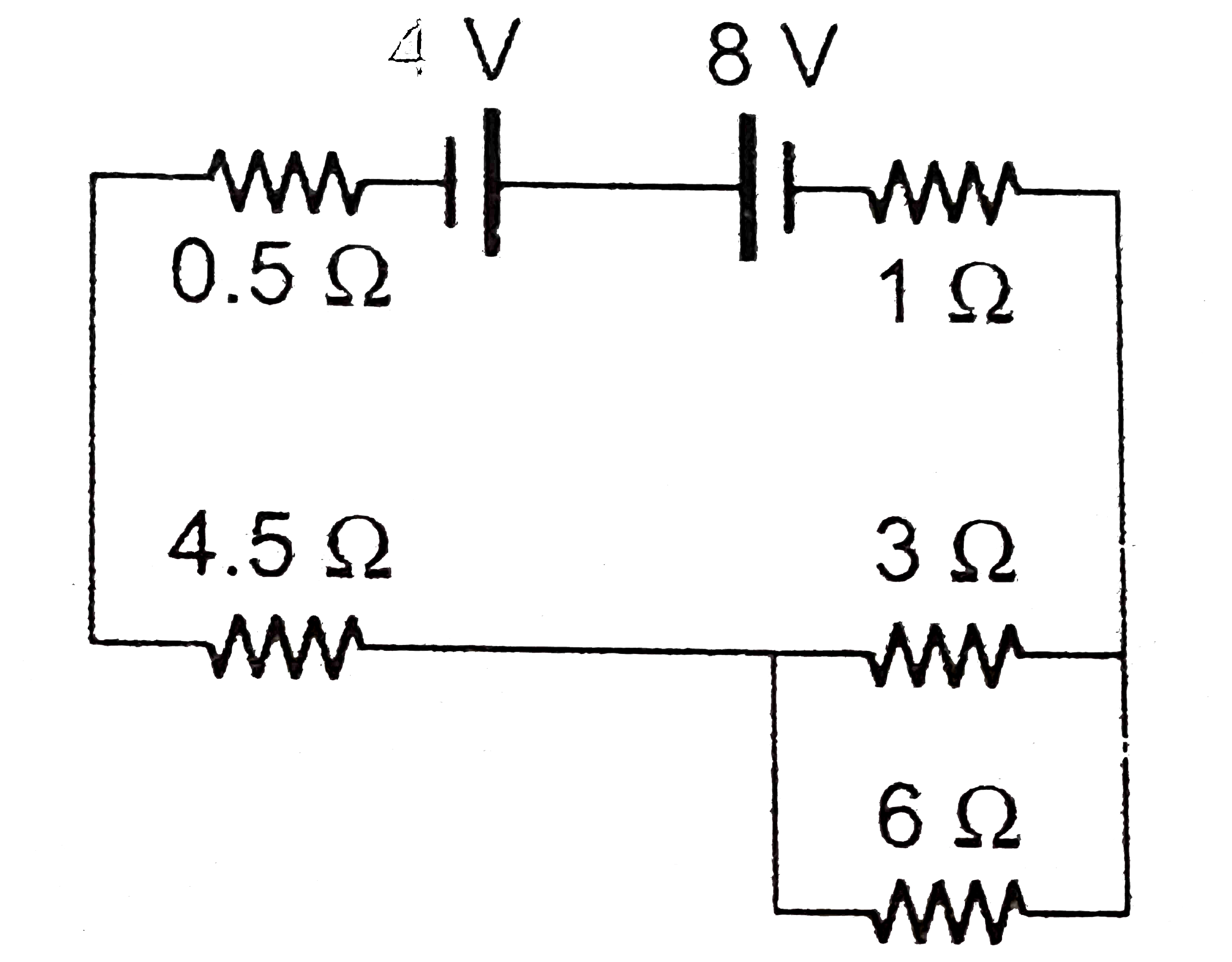
(g) A battery of 6 cells each of emf 2V and internal resistance 0.5Ω is being changed by DC mains of emf 220V by using an external resistance of 10Ω. Calculate.
(i) the charging current
(ii) the potential difference across the battery.
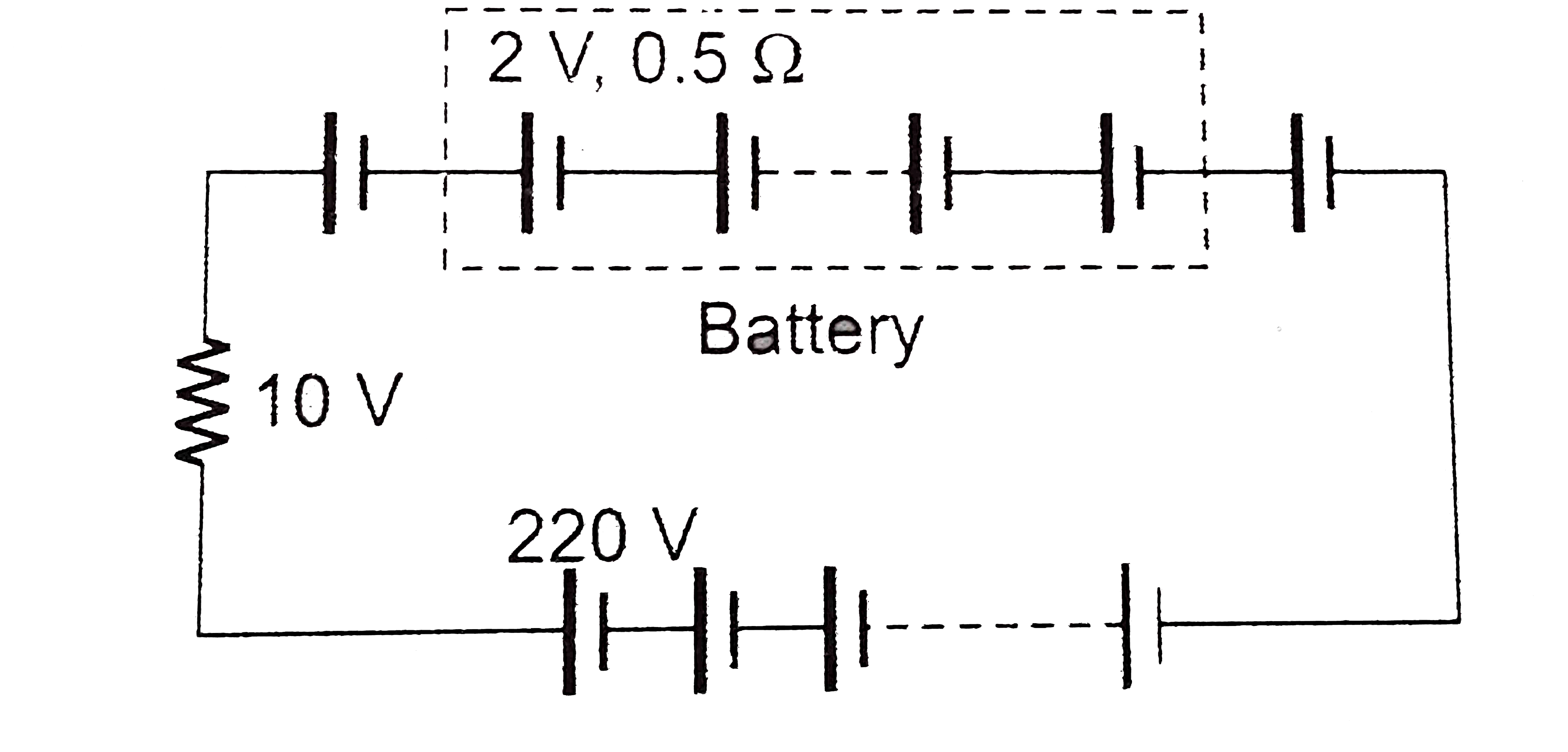 .View Solution
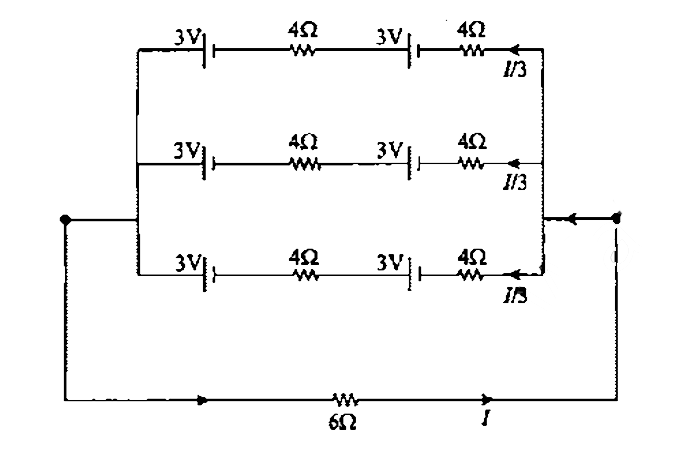
.View SolutionFind current in 6Ω resistance and potential difference across each cell in circuit shown in figure-3.173.
 View Solution
View SolutionFor the resistor network shown in the potential drop between a and b s 12V.
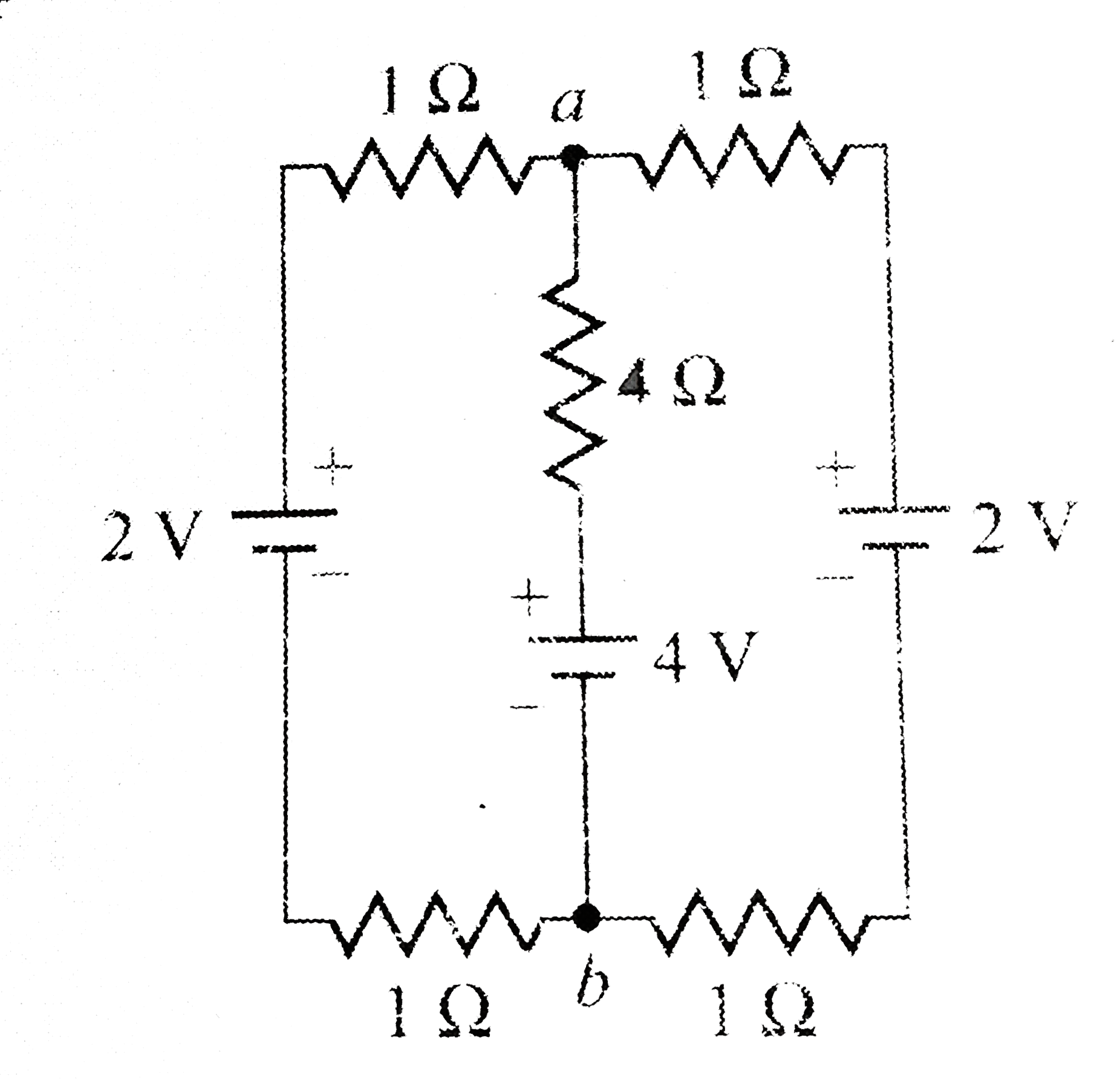
a. Current through resistance of 6Ω is
b. Current through resistance 2Ω is
c. Current through resistance of 8Ω isView Solution