Two conducting wires A and B are made of same material. If the length of B is twice that of A and the radius of circular cross-section of A is twice that of B, then resistances $R_{A} and R_{B}$ are in the ratio

$2 : 1$

$1 : 2$

$1 : 8$

$1 : 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A and B are two square plates of same metal and same thickness but length of B is twice that of A . Ratio of resistances of A and B is

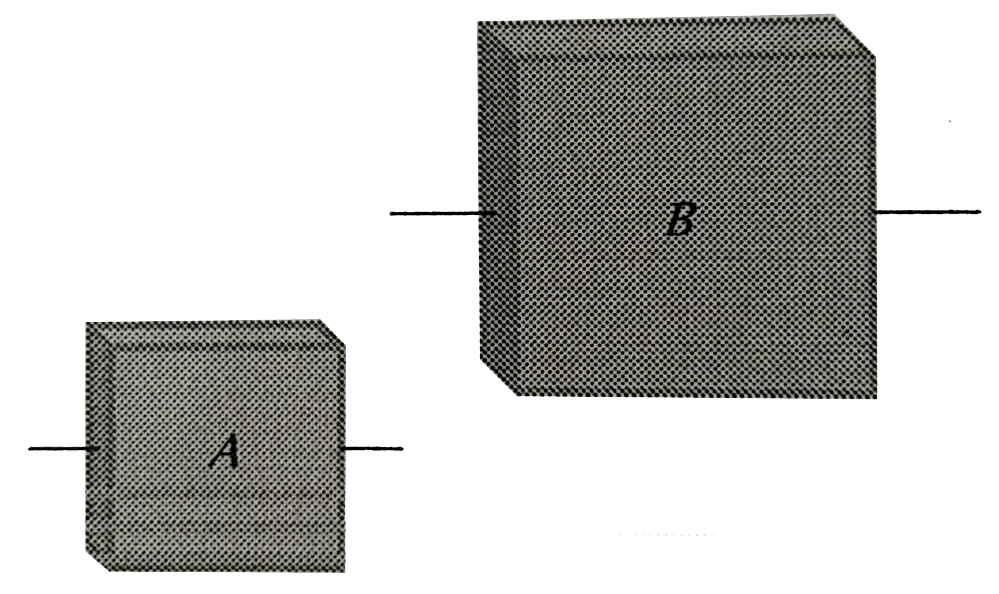A $4 : 1$
B $1 : 4$
C $1 : 1$
D $1 : 2$
Assertion : Two wires A and B have the same cross-sectional area and are made of the same material but the length of wire A is twice that of B. For a given load, the strain in wire A is twice that in B.
Reason : For a given load, the extension in a wire is prportional to its length.
AAssertion is True, Reason is True,
Reason is a correct explanation for Assertion.
BAssertion is True, Reason is True,
Reason is not a correct explanation for Assertion.
CAssertion is True, Reason is False.
DAssertion is False but, Reason is True.
Two planets $A$ and $B$ have the same material density. If the radius of $A$ is twice that of $B$ , then the ratio of the escape velocity $\frac{v_{A}}{v_{B}}$ is
A $2$
B $\sqrt{2}$
C $1 / \sqrt{2}$
D $1 / 2$