No. of Direct and Transverse Common Tangents When $| C_{1} C_{2} | = | r_{1} - r_{2} |$

Video Solution

Text Solution

Generated By DoubtnutGPT

To determine the number of direct and transverse common tangents between two circles when the distance between their centers $| C_{1} C_{2} |$ is equal to $| r_{1} - r_{2} |$ , we can follow these steps:
1. Understanding the Condition:
- We have two circles with centers $C_{1}$ and $C_{2}$ and radii $r_{1}$ and $r_{2}$ respectively.
- The condition given is $| C_{1} C_{2} | = | r_{1} - r_{2} |$ . This means the distance between the centers of the circles is equal to the absolute difference of their radii.
2. Identifying the Type of Tangency:
- When $| C_{1} C_{2} | = | r_{1} - r_{2} |$ , it indicates that the circles are internally touching each other. This means one circle is inside the other and they touch at exactly one point.
3. Determining the Common Tangents:
- For two circles that are internally tangent, there is only one point at which they touch.
- At the point of tangency, there is one direct common tangent that is perpendicular to the line segment joining the centers of the circles at the point of contact.
4. Counting the Tangents:
- Since there is only one point of tangency, there can be:
- Direct Common Tangents: 1 (the tangent at the point of contact)
- Transverse Common Tangents: 0 (there are no transverse tangents because the circles do not have any external tangents when they touch internally)
Final Answer:
- Direct Common Tangents: 1
- Transverse Common Tangents: 0

Updated on:7/8/2024

There are two circles $C_{1}$ and $C_{2}$ whose radii are $r_{1}, r_{2}$ , respectively. If distance between their centre is $3 r_{1} - r_{2}$ and length of direct common tangent is twice of the length of transverse common tangent. Then $r_{1} : r_{2}$ is:
A $5 : 4$
B $6 : 5$
C $7 : 6$
D $8 : 7$
Instruction : Answer the questions given below on the basis following figure.

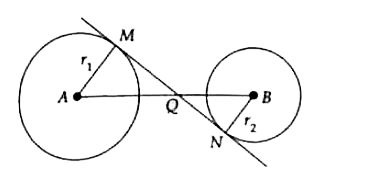
MN is a transverse common tangent. A and B are centres of the circles whose radii are respectively $r_{1} and r_{2}$ . Length of AB is d.
Length of MN is
A $\sqrt{d^{2} - {(r_{1} + r_{2})}_{1}^{2}}$
B $\sqrt{d^{2} - {(r_{1} - r_{2})}_{1}^{2}}$
C $\sqrt{d^{2} + {(r_{1} + r_{2})}_{1}^{2}}$
D $\sqrt{d^{2} + {(r_{1} + r_{2})}_{1}^{2}}$