A body slides without friction from a height H=60cm and then loops the loop of radius R=20cm at the bottom of an incline. Find the ratio of forces exerted on the body by the track at the positions A,B and C(g=10ms−2).
 .
.
From data H=3R
Velocity ar A,VA=√2gH=√2g(3R)=√6gR
Velocity ar B,VB=√4gR
Velocity at C,VC=√2gR
Reaction force at A=R1=mV2AR+mgcos(0∘)
=m×6gRR+mg=7mg
Reaction force at B=R2=mV2BR+mgcos(90∘)
=m×4gRR+0=4mg
Reaction force at C=R3=mV2CR+mgcos(180∘)
=m×2gRR−mg=mg
∴R1:R2:R3=7:4:1.
Topper's Solved these Questions
Similar Questions
A small object slides without friction from the height 5R/2 and then loops of the verticle loop of radius R from which a symmetrical section of angle 2α has been removed. Find angle α such that after losing contact at A and flying through the air, the object will reach point B.

View SolutionA small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
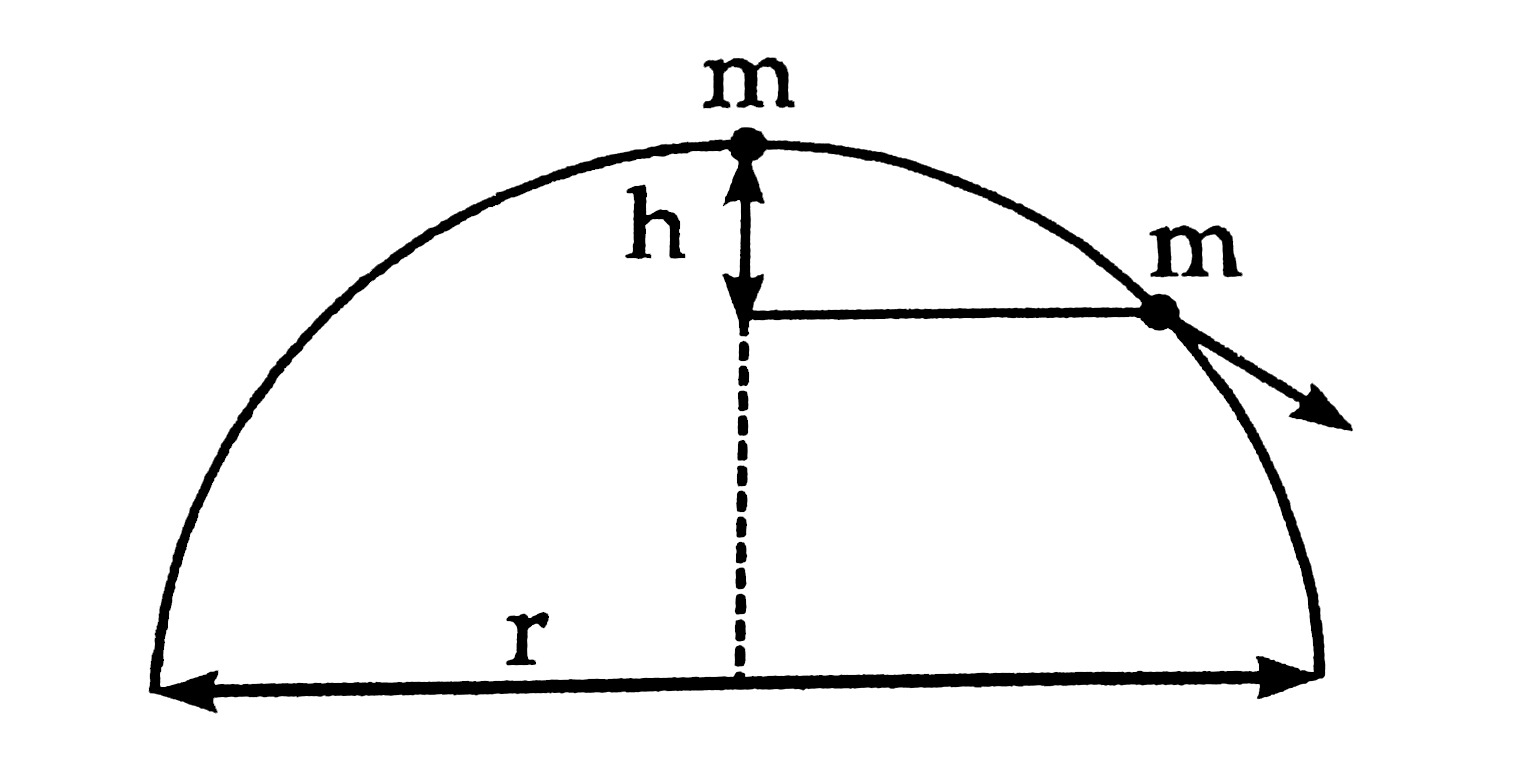
View Solution
Knowledge Check
A body slides down a fixed curved track that is one quadrant of a circle of radius R, as in the figure. If there is no friction and the body starts from rest, its speed at the bottom of the track is
A5gRB√5gRC√2gRD√gRA head slide without friction around a loop the (figure). The bead slide is released is from rest at a height h=3.50R. How large is the normal force on the bead at point (A) if its mass is 50g ?
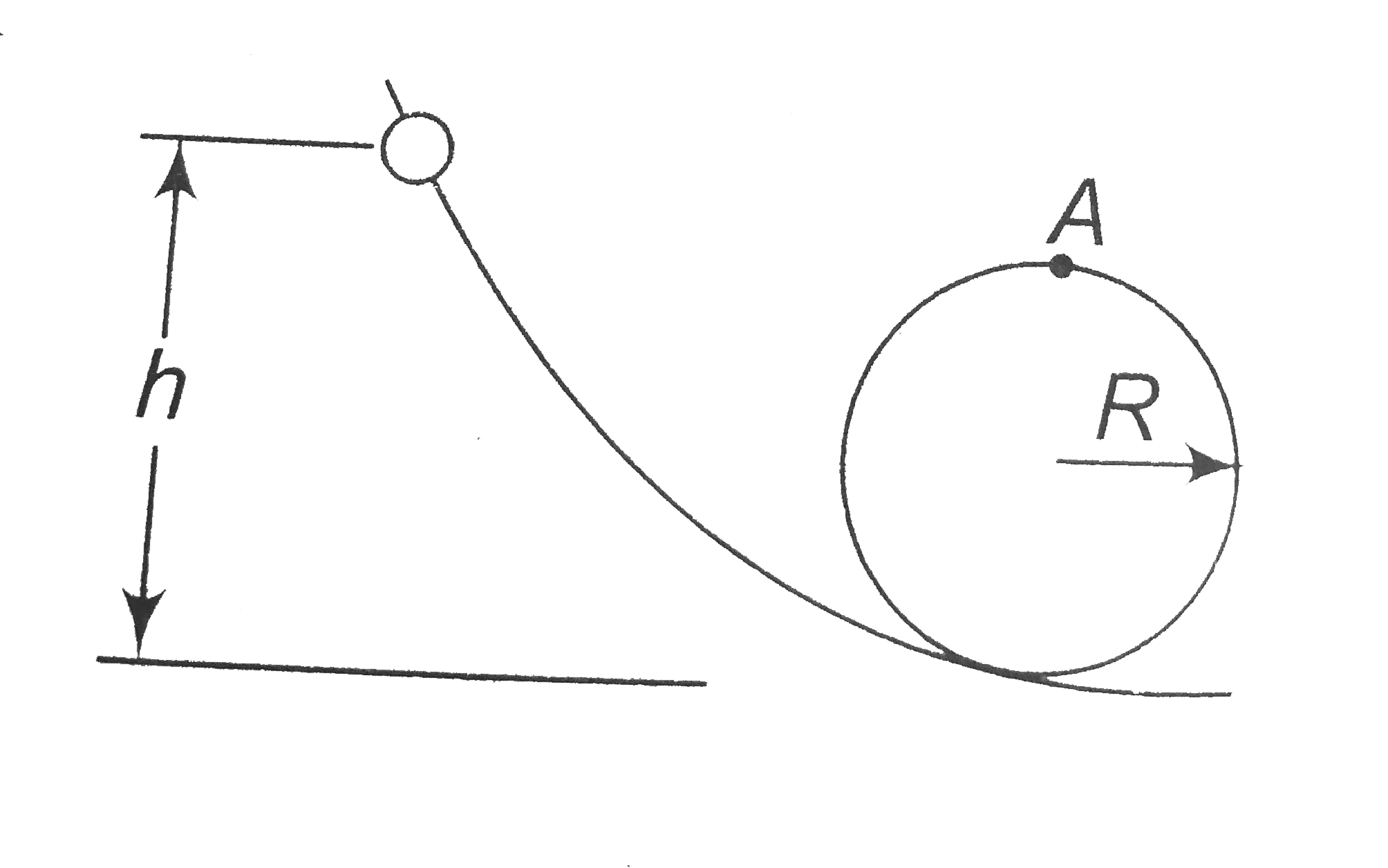 A0.10N downwardB0.10N upwardC1.0N downwardD1.0N upward
A0.10N downwardB0.10N upwardC1.0N downwardD1.0N upwardA water container has water upto a height of 20 cm, volume 2 litres. Top of container has area 60 cm2 and bottom has area of 20 cm2. The downward force exerted by water at the bottom will be.
A200 NB100 NC222 ND122 N
A body slides down an inclined surface which ends into a vertical loop of radius R = 40cm.
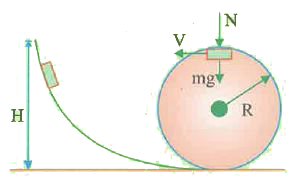
What must be the height H of the inclined surface for the body so that it does not leave contact with the surface even at the uppermost point of the loop? Assume friction to be absent.
View SolutionWater is filled in a flask upto a height of 20cm. The bottom of the flask is circular with radius 10cm. If the atmospheric pressure is 1.013×105 Pa, find the force exerted by the water on the bottom . Take g=10ms−2 and density of water =1000kgm−3.
View SolutionThe block on the loop shown slides without friction. At what height from A it starts so that it passes against the track at B with a net upward force equal to its own weight? The radius of the loop is R.
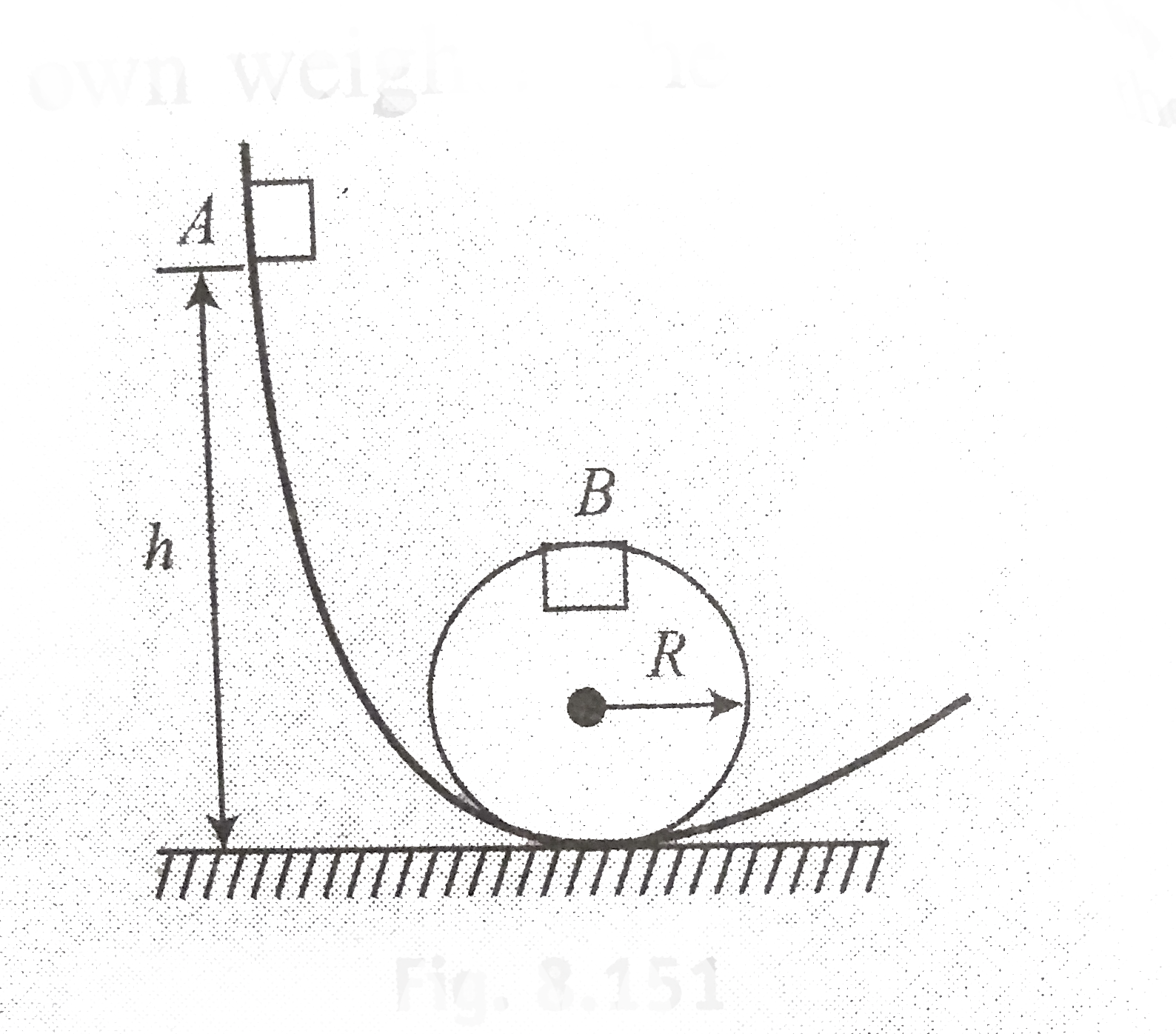
View SolutionA body of mass 10 kg is dropped from a height of 10 m on a planet, whose mass and radius are double that of the Earth. Find the maximum kinetic energy the body can possess.
(TakegE=10ms−2)
View SolutionA small stone of mass 100 g in rotated I a verticlal circle of radius 40 cm. What is the minimum speed needed at the lowest point for looping the loop? Also find the tension in the string at this point (g=10ms−2).
View Solution
