In the figure the variations of componets of acceleration of particles of mass 1kg is shown w.r.t. time. The initial velocity of the particle is m/s. the total work done by the resultant force on the particles in time intervals from t=0 to t=4 seconds is :
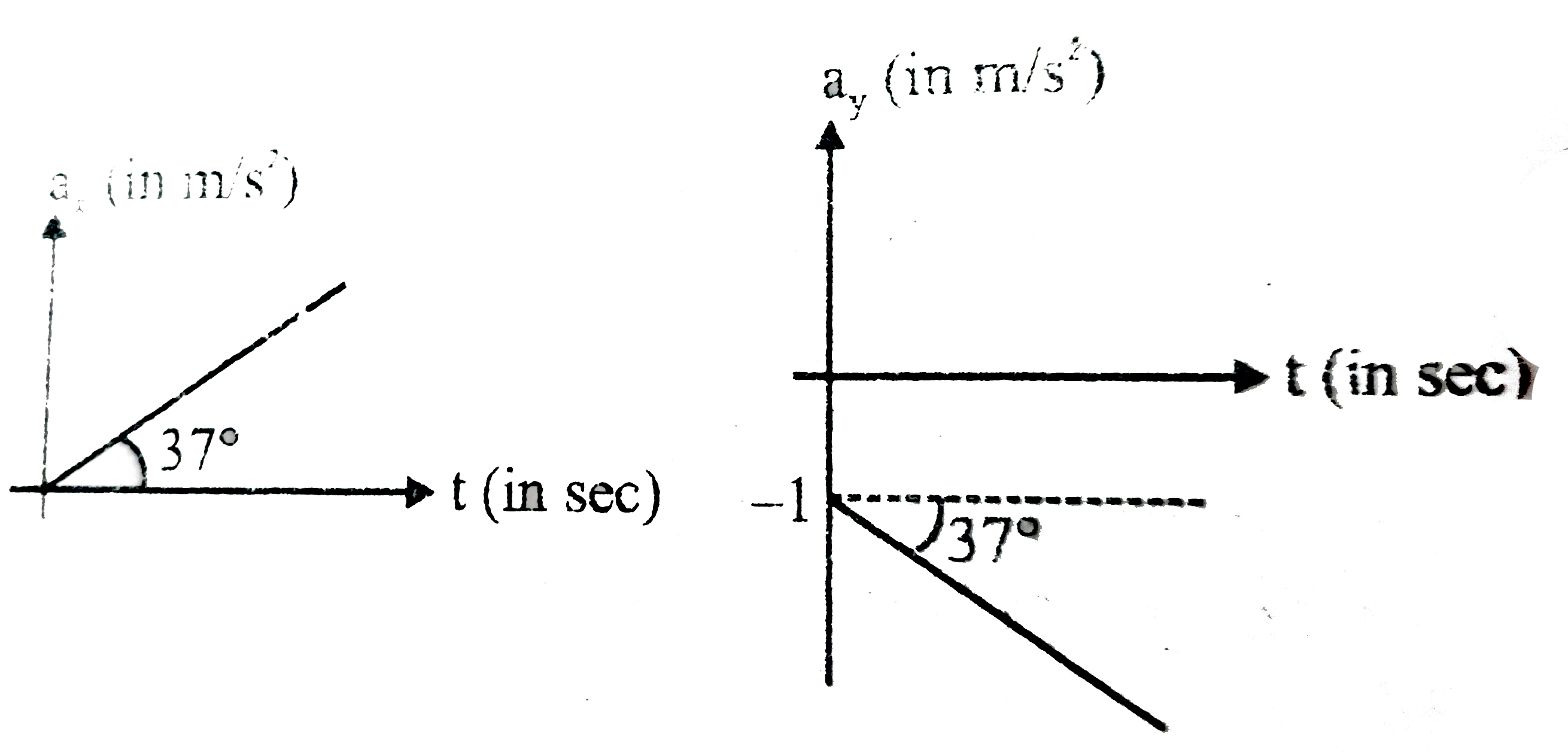
10 J
0
None of these
The correct Answer is:B
From given graphs :
and
At
:. ….(1)
Similarly , ….(2)
As
Alternate Solution :
Area of the graph ,
and
Now work done .
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-V (Multiple Answer)13videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-V (Comprehension)22videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - NCERT (Based Questions)45videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV43videos
WORK , ENERGY & POWER
Similar Questions
Velocity of particle of mass 2kg varies with time t accoridng to the equation →v=(2tˆi+4ˆj)ms−1. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
View SolutionIn the figure, the position time graph of a particle of mass 0.1 kg is shown. The impulse at t=2 second is :
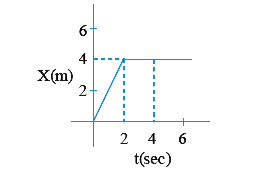 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Velocity of a particle of mass 2kg varies with time t according to the equation →v=(2tˆi+4ˆj)m/s. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
A2ˆim/sB4ˆim/sC8ˆim/sD6ˆim/s - Question 2 - Select One
The velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is
 A(a) 300JB(b) −300JC(c) 400JD(d) −400J
A(a) 300JB(b) −300JC(c) 400JD(d) −400J - Question 3 - Select One
The position vector of a particle is r=asinωtˆi+acosωtˆj
The velocity of the particle isAparallel to position vecorBperpendicular to position vectorCdirected towards originDdirected awa from the origin
Displacement of a particle of mass 2 kg varies with time as s=(2t2−2t+10)m. Find total work done on the particle in a time interval from t=0 to t=2s.
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View SolutionPosition time graph of a particle of mass 2 kg is shown in figrure. Total work done on the particle from t=0 to t=4s is
 View Solution
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
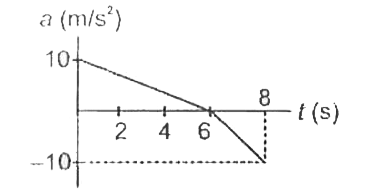 View Solution
View SolutionVelocity-time graph of a particle moving in a straight line is shown in the figure. Mass of the particle is 2 kg. Work done by all the forces acting on the particle in time interval t = 0 to t = 10 sec is
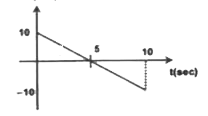 View Solution
View Solution

