Velocity of particle of mass 2kg varies with time t accoridng to the equation $\to v = (2 t ˆ i + 4 ˆ j) m s^{- 1}$ . Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.

Video Solution

Text Solution

Verified by Experts

Impulse=Change in momentum $= m ({\to v}_{2} - {\to v}_{1})$
$= 2 \times [(4 ˆ i + 4 ˆ j) - (4 ˆ j)] = 8 ˆ i k g m s^{- 1}$

Updated on:21/07/2023

Velocity of a particle of mass 2kg varies with time t according to the equation $\to v = (2 t ˆ i + 4 ˆ j) m / s$ . Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
A $2 ˆ i m / s$
B $4 ˆ i m / s$
C $8 ˆ i m / s$
D $6 ˆ i m / s$
In the figure the variations of componets of acceleration of particles of mass 1kg is shown w.r.t. time. The initial velocity of the particle is $\to u = (- 3 ˆ i + 4 ˆ j)$ m/s. the total work done by the resultant force on the particles in time intervals from t=0 to t=4 seconds is :

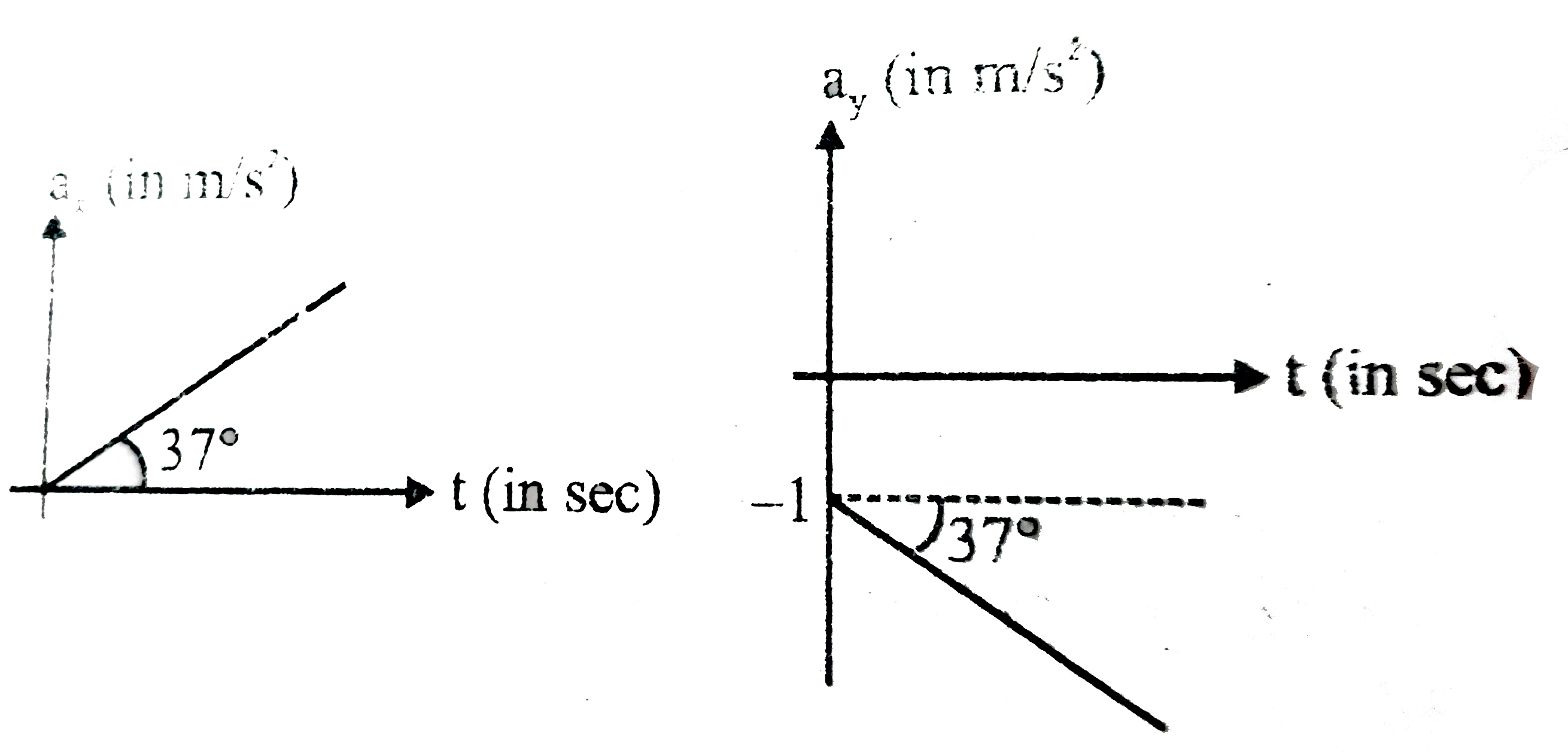A22.5J
B10 J
C0
DNone of these
Velocity of a particle moving in a curvilinear path varies with time as $v = (2 t ˆ i + t^{2} ˆ k) m / s$ . Here t is in second. At $t = 1$ s
Aacceleration of particle is $8 m / s^{2}$
Btangential acceleration of particle is $\frac{6}{\sqrt{5}} m / s^{2}$
Cradial acceleration of particle is $\frac{2}{\sqrt{5}} m / s^{2}$
Dradius of curvature to the path is $\frac{5 \sqrt{5}}{2} m$