A particle $P$ is initially at rest on the top $p f$ a smooth hemispherical surface which is fixed on a horizontal plane. The particle is given a velocity $u$ horizontally. Radius of spherical surface is $a$ .
.

A

If the particle leaves the sphere, when it has fallen vertically by a distance of $\frac{a}{4} m u = \frac{\sqrt{g a}}{2}$ .

B

If the particle leaves the sphere at angle $θ$ (fig) where $cos θ = \frac{\sqrt{3}}{2}$ , then $u = \frac{\sqrt{a g}}{3}$

C

If $u = 0$ and the particle just slides down the hemispherical surface, it will leave the surface when $cos θ = \frac{2}{3}$ .

D

The minimum value of $u$ , for the object to leave the sphere without sliding over the surface is $\sqrt{a g}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C, D

Applying conservation of total energy
$\frac{1}{2} m u^{2} + m g a (1 - c o s θ) = \frac{1}{2} m v^{2}$
$m g cos θ - N = \frac{m v^{2}}{a}$
for particle to lose contact $N = 0$
$v^{2} = a g cos θ, u^{2} + g a (2 - 3 cos θ) = 0$ .

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
Ait will start moving along a circular path if $v < \sqrt{g R}$
Bit will start moving along a circular path if $v > \sqrt{g R}$
Cit will start moving along a parabolic path if $v < \sqrt{g R}$
Dit will start moving along a parabolic path if $v > \sqrt{g R}$
Question 2 - Select One or More
A particle initially at rest on a smooth horizontal surface, is acted on by a constant horizontal force at time $t = 0$ then if W= work, done t=time and v=speed of the particle, the nearly correct graph (s) is //are
A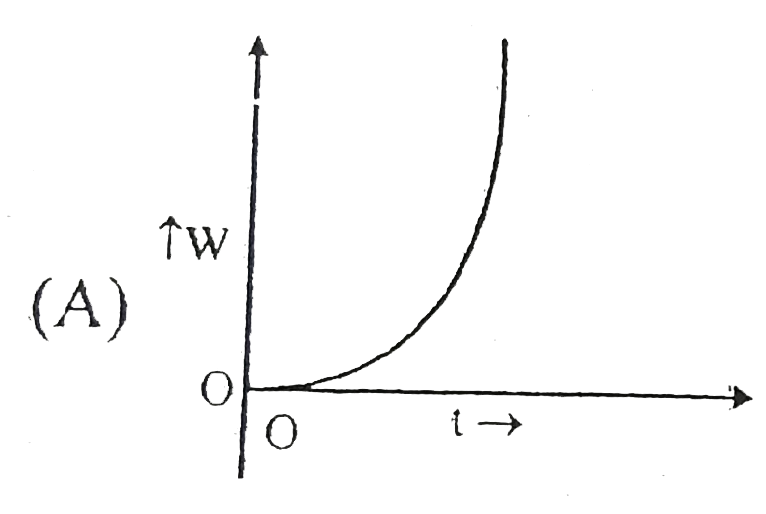
B
C
D
Question 3 - Select One or More
A particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
AThe string becomes slack when the partice reaches its highest point
BThe velocity of the particle becomes zero at the highest point.
CThe kinetic energy of the ball in initial position was $\frac{1}{2} m v^{2} = m \frac{g}{}$
DThe particle again passes through the initial position.

NARAYNA-WORK POWER AND ENERGY-Level-VI (Multiple Answer)

Home
Ask Doubt
Profile