Two particles P and Q move in a straight line AB towards each other. P starts from A with velocity u1 and an acceleration a1 Q starts they pass each other at the midpoint of AB and arrive at the other ends of AB with equal velocities.
they meet at midpoint at time t=2(u2−u1)(a1−a2)
The length of path specified i.e., AB is l=4(u2−u1)(a1u2−a2u1)(a1−a2)2
They reach the other ends of AB with equal velocities if (u2+u1)(a1−a2)=8(a1u2−a2u1)
They reach the other ends of AB with equal velocities if (u2−u1)(a1+a2)=8(a2u1−a1u2)
The correct Answer is:A, B, C
To solve the problem of two particles P and Q moving towards each other and passing at the midpoint of a straight line AB, we will follow these steps:
Step 1: Define the Scenario
Let the distance between points A and B be L. The midpoint, where particles P and Q meet, is at L2.
Step 2: Write the Equations of Motion
For particle P starting from A:
- Initial velocity = u1
- Acceleration = a1
- Distance covered when they meet = L2
Using the equation of motion:
S=ut+12at2
For particle P:
L2=u1t+12a1t2(1)
For particle Q starting from B:
- Initial velocity = u2
- Acceleration = a2
- Distance covered when they meet = L2
Using the same equation of motion:
L2=u2t+12a2t2(2)
Step 3: Equate the Two Equations
From equations (1) and (2), we can set the right-hand sides equal to each other since both equal L2:
u1t+12a1t2=u2t+12a2t2
Step 4: Rearranging the Equation
Rearranging gives:
u1t−u2t=12a2t2−12a1t2
Factoring out t:
t(u1−u2)=12(a2−a1)t2
Assuming t≠0, we can divide both sides by t:
u1−u2=12(a2−a1)t
Step 5: Solve for Time t
Rearranging gives us:
t=2(u1−u2)a2−a1(3)
Step 6: Find the Length of Path L
Substituting t from equation (3) back into either equation (1) or (2) to find L. Using equation (1):
L2=u1(2(u1−u2)a2−a1)+12a1(2(u1−u2)a2−a1)2
This will simplify to find L.
Step 7: Final Condition for Equal Velocities
To find the condition when both particles reach the ends with equal velocities, we can use the final velocity equations:
For particle P:
v21=u21+2a1L
For particle Q:
v22=u22+2a2L
Setting v1=v2 leads to:
u21+2a1L=u22+2a2L
Rearranging gives:
u21−u22=2(a2−a1)L
Conclusion
By substituting the expression for L obtained earlier, we can derive the final condition for equal velocities.
Let the distance between points A and B be L. The midpoint, where particles P and Q meet, is at L2.
For particle P starting from A:
- Initial velocity = u1
- Acceleration = a1
- Distance covered when they meet = L2
S=ut+12at2
For particle P:
L2=u1t+12a1t2(1)
- Initial velocity = u2
- Acceleration = a2
- Distance covered when they meet = L2
L2=u2t+12a2t2(2)
From equations (1) and (2), we can set the right-hand sides equal to each other since both equal L2:
u1t+12a1t2=u2t+12a2t2
Rearranging gives:
u1t−u2t=12a2t2−12a1t2
Factoring out t:
t(u1−u2)=12(a2−a1)t2
Assuming t≠0, we can divide both sides by t:
u1−u2=12(a2−a1)t
Rearranging gives us:
t=2(u1−u2)a2−a1(3)
Substituting t from equation (3) back into either equation (1) or (2) to find L. Using equation (1):
L2=u1(2(u1−u2)a2−a1)+12a1(2(u1−u2)a2−a1)2
This will simplify to find L.
To find the condition when both particles reach the ends with equal velocities, we can use the final velocity equations:
For particle P:
v21=u21+2a1L
For particle Q:
v22=u22+2a2L
Setting v1=v2 leads to:
u21+2a1L=u22+2a2L
Rearranging gives:
u21−u22=2(a2−a1)L
By substituting the expression for L obtained earlier, we can derive the final condition for equal velocities.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Integer Type Question13videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Single Answer Question8videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Passage Type Questions16videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)31videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
Similar Questions
Two points P and Q move in a straight line AB. The point P starts from A in the direction AB with velocity u and acceleration f and at the same time Q starts from b in the direction of BA with velocity u1 and acceleration f1. If they pass one another at the middle point of AB and arrive at the other ends of AB with equal velocities, then (u+u1)(f−f1)=8(fu1−f1u).
View SolutionTwo trucks are moving in a straight line towards each other at initial velocities u1 and u2 and with constant retardations a1 and a2. If the initial separation between them is d, find the minimum value of d for no collision.
View Solution
Knowledge Check
- Question 1 - Select One
Two particles P and Q are projected simultaneously away from each other from a point A as shown in figure. The velocity of P relative to Q in ms−1 at the instant when the motion of P is horizontal is
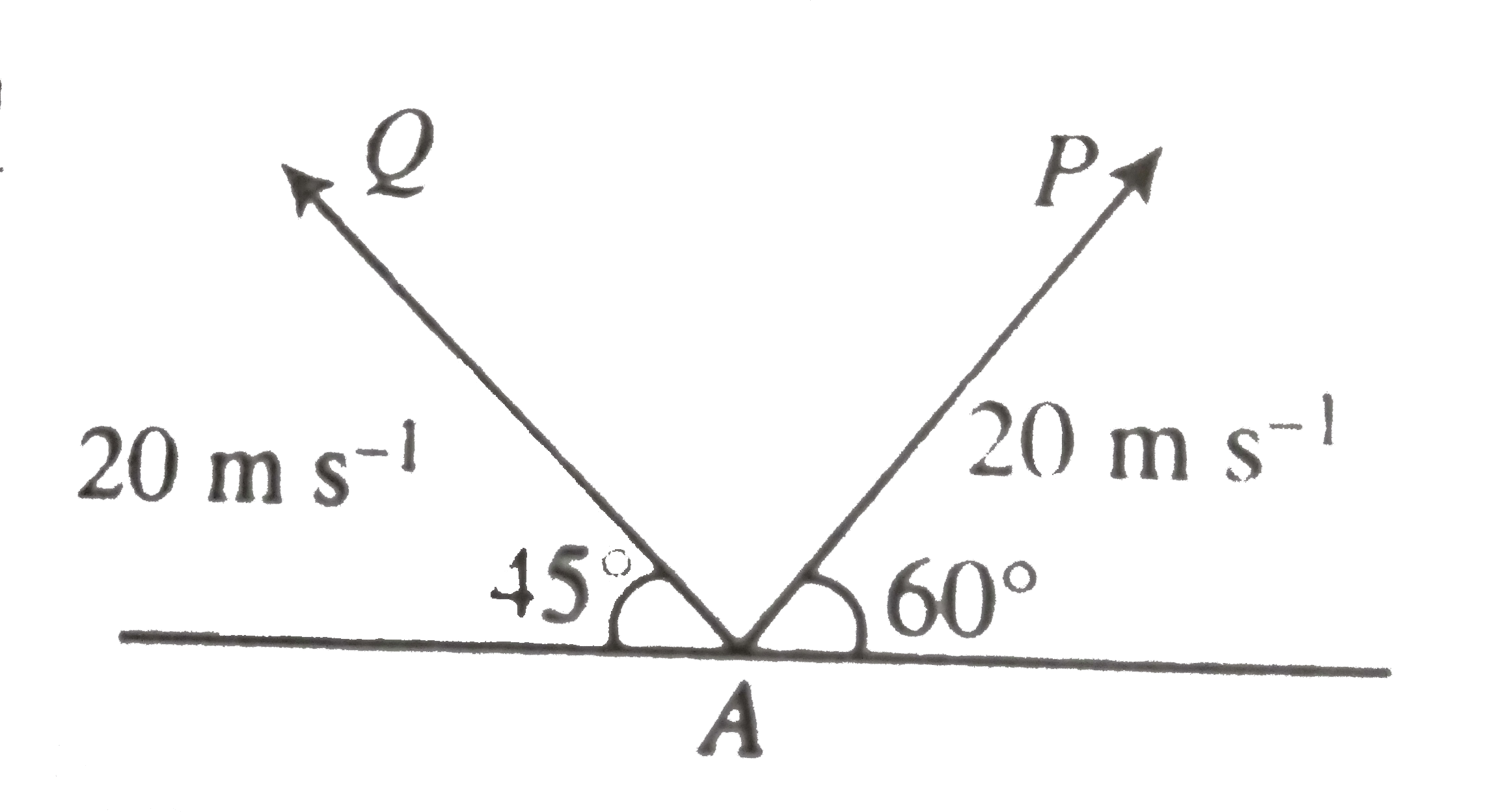 A10√4−√3B20√4−√3C10√4+√3D20√4+√3
A10√4−√3B20√4−√3C10√4+√3D20√4+√3 - Question 2 - Select One
Two particles start simultaneously from the same point and move along two straight lines. One with uniform velocity v and other with a uniform acceleration a. if α is the angle between the lines of motion of two particles then the least value of relative velocity will be at time given by
AvasinαBvacosαCvatanαDvacotα - Question 3 - Select One
A particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
A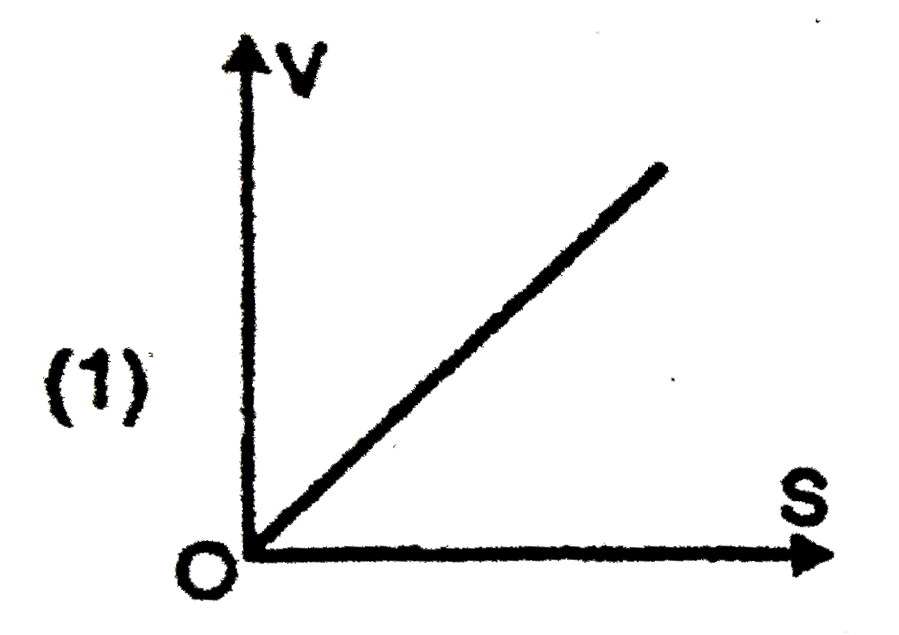 B
B C
C D
D
Two trucks are moving in a straight line towards each other at initial velocities u1 and u2 and with constant retardations a1 and a2. If the initial separation between them is d, find the minimum value of d for no collision.
View SolutionA particle moves along a straight line AB with constant acceleration. Its velocities are u and v at A and B, respectively. Show that its velocity at the mid-point of AB is √u2+v22.
View SolutionA particle P is moving along a straight line with a velocity of 3ms−1 and another particle Q has a velocity of 4ms−1 at an angle of 30∘ to the path of P. Find the speed of Q relative to P.
View SolutionTwo cacar starts together from the asme point and move along two straight lines inclined at an angle θ, one moving with velocity (u) and the other from rest with a uniform acceleration (a). Show that the least relative velocity between then is usinθ and it occurs after a time t=(ucosθ)/a.
View SolutionTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View Solution

