Injective function(one-one function) and Many-one function
What is Injective function(one-one function) and Many-one function?
Functions are classified according to their images and pre-images relationships. Let’s see the function x → f(x) = y with domain A and co-domain B.
If for each x ε A there exist only one image y ε B and each y ε B has a unique pre-image x ε A (i.e. no two elements of A would have the same image in B), then ‘f’ is said to be one-one function. Otherwise, f is a many-to-one function.
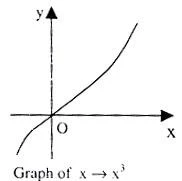
e.g. x → x3, x ε R is one-one function
while x → x2, x ε R is many-to-one function. (see figure above)
e.g. x = + 2, y = x2 = 4
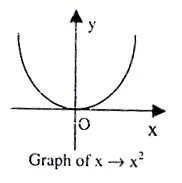
Graphically, if a line parallel to x axis cuts the graph of f(x) at more than one point then f(x) is many-to-one function and if a line parallel to y-axis cuts the graph at more than one place, then it is not a function.
For a one-to-one function
If x1 ≠ x2 then f(x1) ≠ f(x2)
or if (x1) = f(x2) => x1 = x2
One-to-one mapping is called injection (or injective).
Mapping (when a function is represented using Venn-diagrams then it is called mapping), defined between sets X and Y such that Y has at least one element 'y' which is not the f-image of X are called into mappings.
Let a function be defined as: f : X → Y
Where X = {2, 3, 5, 7} and Y = {3, 4, 6, 8, 9, 11}
The mapping is shown in the figure below.
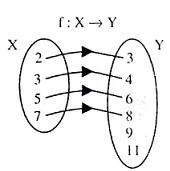
Clearly, element 9 and 11 of Y are not the f-image of any of x ε X
So the mapping is into-mapping
Hence for into mappings:
f[X}  Y and f[X] ≠ Y. => f [X]
Y and f[X] ≠ Y. => f [X]  Y that is range is not a proper subset of co-domain.
Y that is range is not a proper subset of co-domain.
The mapping of 'f' is said to be onto if each element of Y is the f-image of at least one element of X. Onto mapping are also called surjection.
One-one and onto mapping are called bijection.
Illustration
Check whether y = f(x) = x3; f : R → R is one-one/many-one/into/onto function.
We are given domain and co-domain of 'f' as a set of real numbers.
For one-one function:
Let x1, x2 ε Df and f(x1) = f(x2)
=>X13 =X23
=> x1 = x2
i.e. f is one-one (injective) function.
For onto-into:
Ltx→a y = Ltx→a (x)3 = α
Ltx→a y = Ltx→a (X)3 = -α
Therefore y = x3 is bijective function.
Illustration:
What kind of function does the Venn diagram in figure given below represent?

Solution: This many-one into function
Domain = Df = {a, b, c}
Co-domain = {1, 2, 3}
Range = Rf = {1, 2}
f(a) = 1 ; f(b) = 2; f(c) = 2
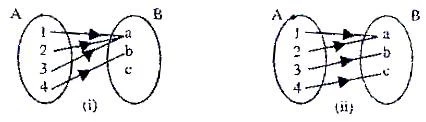
Examples
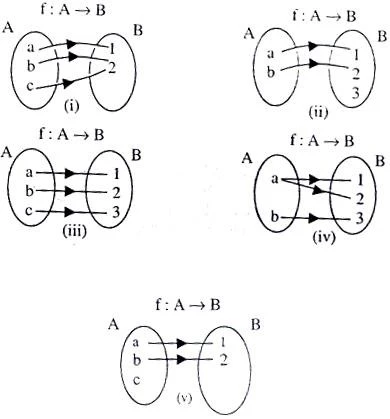
Ans.
(i) Many-one and onto (surjective).
(ii) One-one (injective) and into.
(iii) One-one (injective) and onto (surjective) i.e. Bijective.
(iv)and(v)arenotfunctions.
Examples:
1. Given the sets A = {1, 2, 3, 4} and B = {a, b, c} construct a
(i) Many-one into
(ii) Many-one onto function
2. Given the sets c = {1, 2, 3} and D = {a, b, c}
(i) How many one-one onto functions can be constructed?
(ii) How many-one into functions can be constructed?
Ans.1
f : A → B f : A → B
2. (i) 6
(ii) 33 - 6 = 21
Illustration:
What is the domain and range of the following functions?
(a) y = 3x + 5 (b) y = (x2 +x)/(x2 - x)
Domain of y = f(x) is the set of values of x for which y is real and finite.
Range is the set of values of y for which x is real and finite.
Solution:
(a) For all real and finite x, y is also real and finite
Therefore Df = R = (-∞, ∞) and Rf = R = (-∞,∞)
(b) y = (x(x+1))/(x(x-1)) = (x+1)/(x-1) , x ≠ 0
when x = 0, y is 0/0 from (i.e. indetermined form)
when x = 1, y = ∞ (infinite)
Therefore Df = R -{0, 1}
also xy - y = x + 1
=> x (y - 1) = y + 1
x = (y+1)/(y-1)
when y = 1, x = ∞ (infinite) => y ≠ 1
also, for ≠ 0 => y ≠ -1
Therefore Rf = R - {-1, 1}
Illustration:
What is the domain of the following functions?
(a) y =√((x-1)(3-x)) (b) √(((x-1)(x-5))/(x-3)) (c) y = √sin x
Solution:
(a) y is real and finite if (x - 1)(3 - x) > 0
or (x - 1)(x - 3) < 0
i.e. x - 1 < 0 and x - 3 > 0 or x - 1 > 0 and x - 3 < 0
=> x < 1 and x > 3 => 1 < x < 3
which is not possible => 1 < x < 3
=> Df = [1, 3]
(b) Numerator becomes zero for x = 1, x = 5
Denominator becomes zero for x = 3
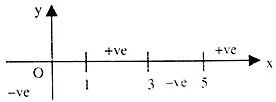
These three points divide x-axes into four intervals
(-∞, 1), (1, 3), (3, 5), (5, ∞)
Therefore Df = [1, 3) υ [5, ∞); at x = 3, we here open interval,
Because at x = 3, y is infinite.
(c) y = √sin x
sin x > 0 ∀ x ε [2n∏, (2n + 1) ∏], n ε I
Examples:
1. What is domain of the following?
Df = [1, 3)
(b) Df = [-(2n-1)∏, - (a) y =√((x-1)(3-x)) (b) y = √xsinx (c) y = Sin-1((1+x2)/(2x))
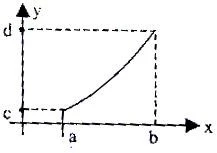
2. What is domain and range of the following?
(a)
(b) y =|x
Ans.
1. (a)
2(n-1)∏] υ [2n ∏, (2n + 1)∏], n ε N
(c) Df = {-1, 1}
2. (a) Df = [a, b[ and Rf = [c, d]
(b) Df = {0, 1, 2, 3, 4,......}
Rf = {1, 2, 6, 24, ......}




Examples


2. What is domain and range of the following?

Similar Questions
Knowledge Check
Statement-1 : If f(x) and g(x) are one-one functions then f(g(x)) and g(f(x)) is also a one-one function.
and
Statement-2 The composite function of two one-one function may or many not be one-one.AStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1.CStatement -1 is True, Statement -2 is FalseDStatement -1 is False, Statement -2 is True
Number of One One and many one functions
View SolutionAlgorithm of one-one function
View SolutionLet f:R−{n}→R be a function defined by f(x)=x−mx−n such that m≠n 1) f is one one into function2) f is one one onto function3) f is many one into funciton4) f is many one onto funcionn then
View SolutionGive one function of SER
View SolutionMark (a) if function is one - one and into Mark (b) if function is one - one but not into Mark (c) if function is neither one - one nor into Mark (d) if function is not one - one but into
f(x)=x2
f:R→R+∪{0}
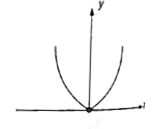
View SolutionMark (a) if function is one - one and into
Mark (b) if function is one - one but not into
Mark (c) if function is neither one - one nor into
Mark (d) if function is not one - one but into
f(x)=x2
f:R→R

View SolutionMark (a) if function is one - one and into
Mark (b) if function is one - one and not into
Mark (c) if function is not one - one and into
Mark (d) if function is not one - one and not into
f(x)=x2
f:R+→R+
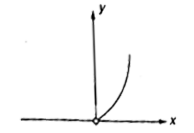
View Solution
