How to determine that function is one one or many one
How to determine that function is one one or many one?
Functions are classified according to their images and pre-images relationships. Let’s see the function x → f(x) = y with domain A and co-domain B.
If for each x ε A there exist only one image y ε B and each y ε B has a unique pre-image x ε A (i.e. no two elements of A would have the same image in B), then ‘f’ is said to be one-one function. Otherwise, f is a many-to-one function.
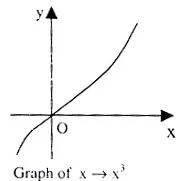
e.g. x → x3, x ε R is one-one function
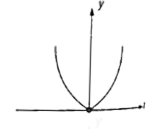
while x → x2, x ε R is many-to-one function. (see figure above)
e.g. x = + 2, y = x2 = 4
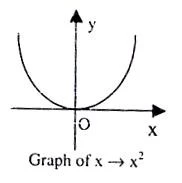
Graphically, if a line parallel to x axis cuts the graph of f(x) at more than one point then f(x) is many-to-one function and if a line parallel to y-axis cuts the graph at more than one place, then it is not a function.
For a one-to-one function
If x1 ≠ x2 then f(x1) ≠ f(x2)
or if (x1) = f(x2) => x1 = x2
One-to-one mapping is called injection (or injective).
Mapping (when a function is represented using Venn-diagrams then it is called mapping), defined between sets X and Y such that Y has at least one element 'y' which is not the f-image of X are called into mappings.
Let a function be defined as: f : X → Y
Where X = {2, 3, 5, 7} and Y = {3, 4, 6, 8, 9, 11}
The mapping is shown in the figure below.
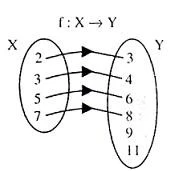
Clearly, element 9 and 11 of Y are not the f-image of any of x ε X
So the mapping is into-mapping
Hence for into mappings:
f[X}  Y and f[X] ≠ Y. => f [X]
Y and f[X] ≠ Y. => f [X]  Y that is range is not a proper subset of co-domain.
Y that is range is not a proper subset of co-domain.
The mapping of 'f' is said to be onto if each element of Y is the f-image of at least one element of X. Onto mapping are also called surjection.
One-one and onto mapping are called bijection.
Illustration
Check whether y = f(x) = x3; f : R → R is one-one/many-one/into/onto function.
We are given domain and co-domain of 'f' as a set of real numbers.
For one-one function:
Let x1, x2 ε Df and f(x1) = f(x2)
=>X13 =X23
=> x1 = x2
i.e. f is one-one (injective) function.
For onto-into:
Ltx→a y = Ltx→a (x)3 = α
Ltx→a y = Ltx→a (X)3 = -α
Therefore y = x3 is bijective function.
Illustration:
What kind of function does the Venn diagram in figure given below represent?
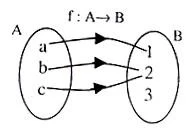
Solution: This many-one into function
Domain = Df = {a, b, c}
Co-domain = {1, 2, 3}
Range = Rf = {1, 2}
f(a) = 1 ; f(b) = 2; f(c) = 2
Examples
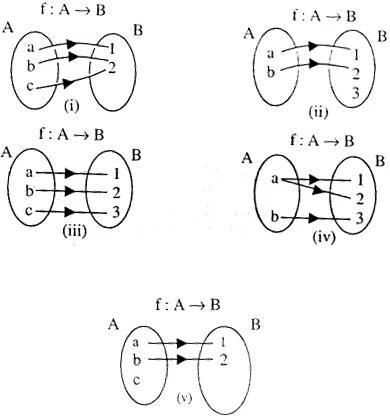
Ans.
(i) Many-one and onto (surjective).
(ii) One-one (injective) and into.
(iii) One-one (injective) and onto (surjective) i.e. Bijective.
(iv)and(v)arenotfunctions.
Examples:
1. Given the sets A = {1, 2, 3, 4} and B = {a, b, c} construct a
(i) Many-one into
(ii) Many-one onto function
2. Given the sets c = {1, 2, 3} and D = {a, b, c}
(i) How many one-one onto functions can be constructed?
(ii) How many-one into functions can be constructed?
Ans.1
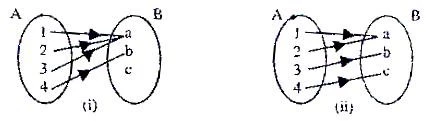
f : A → B f : A → B
2. (i) 6
(ii) 33 - 6 = 21
Illustration:
What is the domain and range of the following functions?
(a) y = 3x + 5 (b) y = (x2 +x)/(x2 - x)
Domain of y = f(x) is the set of values of x for which y is real and finite.
Range is the set of values of y for which x is real and finite.
Solution:
(a) For all real and finite x, y is also real and finite
Therefore Df = R = (-∞, ∞) and Rf = R = (-∞,∞)
(b) y = (x(x+1))/(x(x-1)) = (x+1)/(x-1) , x ≠ 0
when x = 0, y is 0/0 from (i.e. indetermined form)
when x = 1, y = ∞ (infinite)
Therefore Df = R -{0, 1}
also xy - y = x + 1
=> x (y - 1) = y + 1
x = (y+1)/(y-1)
when y = 1, x = ∞ (infinite) => y ≠ 1
also, for ≠ 0 => y ≠ -1
Therefore Rf = R - {-1, 1}




Examples


Similar Questions
Find whether the following function are one-one or many -one & into or onto if f:D→R where D is its domain
f(x)=xcosx
View SolutionFind whether the function are one–one or many–one
f(x)=sin4x,x∈(−π8,π8)
View SolutionFind whether the following function are one-one or many -one & into or onto if f:D→R where D is its domain
f(x)=1sin√|x|
View SolutionFind whether the following function are one-one or many -one & into or onto if f:D→R where D is its domain
f(x)=|lnx|
View SolutionFind whether the function are one–one or many–one
f(x)=3x24π−cosπx
View SolutionFind whether the following functions are one-one or many-one f(x)=√1−e1x−1
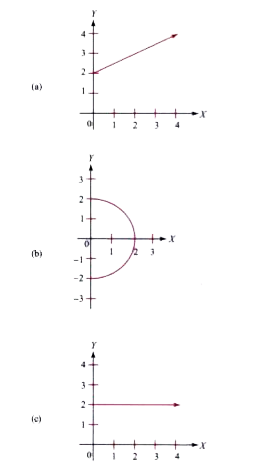
View SolutionThe diagrams given below represent relations from X to Y. Classify them as relation or function. If the relation is a function, classify it as one - one or many - one.
View SolutionLet f:R−{n}→R be a function defined by f(x)=x−mx−n such that m≠n 1) f is one one into function2) f is one one onto function3) f is many one into funciton4) f is many one onto funcionn then
View SolutionMark (a) if function is one - one and into
Mark (b) if function is one - one but not into
Mark (c) if function is neither one - one nor into
Mark (d) if function is not one - one but into
f(x)=x2
f:R→R
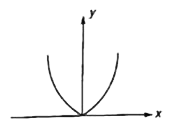
View SolutionMark (a) if function is one - one and into Mark (b) if function is one - one but not into Mark (c) if function is neither one - one nor into Mark (d) if function is not one - one but into
f(x)=x2
f:R→R+∪{0}
View Solution
